【Codeforces858F】Wizard's Tour [构造]

Wizard's Tour

Time Limit: 50 Sec  Memory Limit: 512 MB

Description

　　

Input

　　

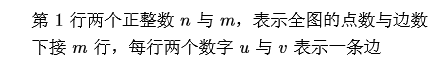
Output

　　

Sample Input

　　4 5
　　1 2
　　3 2
　　2 4
　　3 4
　　4 1

Sample Output

　　2
　　4 1 2
　　4 3 2

HINT

　　

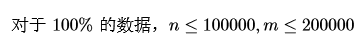
Solution

　　首先，一个连通块的答案可以是floor(m / 2)。考虑如何构造出一种解。

　　首先我们先搞出一个dfs树。

　　那么现在对于一个点，有三种边：1. 非树边；2. 儿子边；3. 父亲边。

　　我们将非树边和儿子边的优先级看做一样的，父亲边优先级最低。

　　考虑将边配给点，即这个点是一种走法中的中点。从叶子节点往上做。两两配对这些边。

　　显然每条边都被尽可能利用了，最后只有与根相连的边可能会有最多一条用不了。

　　这样就是一种解了。

Code

 #include<iostream>
 #include<string>
 #include<algorithm>
 #include<cstdio>
 #include<cstring>
 #include<cstdlib>
 #include<cmath>
 #include<vector>
 using namespace std;
 typedef long long s64;

 const int ONE = ;
 const int MOD = 1e9 + ;

 int get()
 {
         int res = , Q = ; char c;
         while( (c = getchar()) <  || c > )
             if(c == '-') Q = -;
         if(Q) res = c - ;
         while( (c = getchar()) >=  && c <= )
             res = res *  + c - ;
         return res * Q;
 }

 int ans_len;
 struct power
 {
         int l, mid, r;
 }Ans[ONE * ];

 int n, m;
 int x, y;
 int next[ONE * ], first[ONE], go[ONE * ], tot;
 int vis[ONE * ];

 void Add(int u, int v)
 {
         next[++tot] = first[u], first[u] = tot, go[tot] = v;
         next[++tot] = first[v], first[v] = tot, go[tot] = u;
 }

 vector <power> A;
 int fat[ONE];

 void Dfs(int u)
 {
         for(int e = first[u]; e; e = next[e])
         {
             int v = go[e];
             if(fat[v] || vis[e]) continue;
             fat[v] = u, Dfs(v);
         }

         A.clear();
         for(int e = first[u]; e; e = next[e])
             if(!vis[e] && fat[u] != go[e]) A.push_back((power){go[e], , e});
         for(int e = first[u]; e; e = next[e])
             if(!vis[e] && fat[u] == go[e]) A.push_back((power){go[e], , e});

         int p = , len = A.size();
         for(int j = ; j +  < len; j += )
         {
             vis[A[j].r] = vis[(A[j].r-^)+] = ;
             vis[A[j+].r] = vis[(A[j+].r-^)+] = ;
             Ans[++ans_len] = (power){A[j].l, u, A[j + ].l};
         }
 }

 int main()
 {
         n = get();    m = get();
         for(int i = ; i <= m; i++)
             x = get(), y = get(), Add(x, y);

         for(int i = ; i <= n; i++)
             if(!fat[i]) Dfs(i);

         printf("%d\n", ans_len);
         for(int i = ; i <= ans_len; i++)
             printf("%d %d %d\n", Ans[i].l, Ans[i].mid, Ans[i].r);
 }