安徽师大附中%你赛day5 T3 树上行走 解题报告

树上行走

题目背景

\(\mathrm{Smart}\) 的脑洞非常大， 经常幻想出一些奇怪的东西。

题目描述

某一天，\(\mathrm{Smart}\) 幻想出了一棵没有边际的二叉树，脑补着在那棵二叉树上行走的场景。

\(\mathrm{Smart}\) 一开始在二叉树的根， 然后 \(\mathrm{Smart}\) 写下了一个由'L','R'两种字符构成的串，他称这个串为初始串，按照这个串的顺序， 碰到一个'L'就移动到左儿子，碰到一个'R' 就移动到右儿子。

\(\mathrm{Smart}\) 最后的位置就是他接下来操作的起点。

然后 \(\mathrm{Smart}\) 有写下一个串，他称这个串为操作串，由'U','L','R'三种字符构成，'U'表示移动到当前点的父亲（特殊地， 我们定义根节点

的父亲为根自己） ,'L','R'同上。

但是 \(\mathrm{Smart}\) 觉得直接按照操作串一步一步走十分无聊，所以 \(\mathrm{Smart}\) 会跳过一些操作（心情不好的时候也可能跳过所有操作， 或不跳过） ，现在 \(\mathrm{Smart}\) 想知道他会走到多少种可能的终点。 由于答案可能很大， 所以只需输出答案\(\mod 1,000,000,007\)的值。

输入输出格式

输入格式

第一行一个由'L','R' 两种字符构成的串。

第二行一个由'U','L','R' 三种字符构成的串。

输出格式

说明：

输出一行，为答案\(\mod 1000000007\)。

\(30\%\)的数据： 初始串长度\(\le 10\)，操作串长度\(\le 5\)；

\(50\%\)的数据： 初始串长度\(\le 100\)， 操作串长度\(\le 10\)；

另有\(20\%\)的数据： 操作串中没有'U'操作。

\(100\%\)的数据： 初始串长度\(\le 10^5\)，操作串长度\(\le 10^5\)。

---

感觉非常神的一题，考试时至少想了两个小时无果。

想的是特殊数据，知道特殊数据了以后其实好做了

其间想过 几种简单DP 容斥 打表 子问题分治 字典序（康拓）展开 特殊情况找规律 几个方法 全凉了

事实上后面一段时间我一直在想“一个01串有多少种不同的子序列？”这个抽象的问题，殊不知，原本的题目给出的模型和解法更加贴近。

我们先给出一个大题的思路，然后具体讲解。

将答案分成2^字符集大小的容器进行统计

具体的，我们把统计的节点分为以下4类

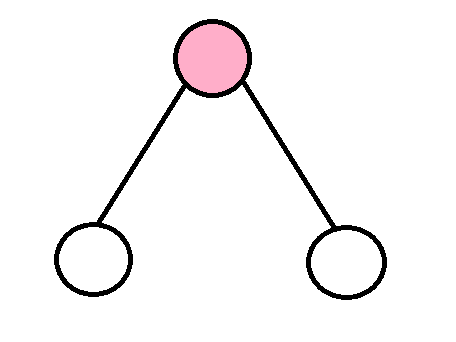
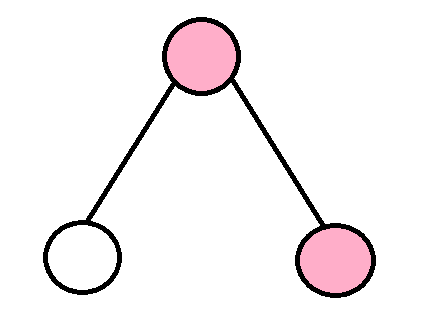
分别代表：左右儿子都没去过的点，只去过左儿子的点，只去过右儿子的点，两个儿子都去过的点

我们用容器分别存这四类点的个数

然后从左往右做操作，更新谁谁走成了谁睡

如果加入'U'其实也很简单

只有最开始的'U'是有用的，把最开始的操作存起来，然后碰到一个就倒着弹出一个，更新某个状态就行啦

---

Code:

#include <cstdio>
#include <cstring>
#define ll long long
const ll mod=1e9+7;
const int N=1e5+10;
char t[N],s[N];
int tot;
ll dp[4];
int main()
{
    scanf("%s",s+1);
    tot=strlen(s+1);
    scanf("%s",t);
    int n=strlen(t);
    dp[0]=1;
    for(int i=0;i<n;i++)
    {
        if(t[i]=='L')
        {
            (dp[1]+=dp[0])%=mod;
            (dp[0]+=dp[2])%=mod;
            (dp[3]+=dp[2])%=mod;
            dp[2]=0;
        }
        else if(t[i]=='R')
        {
            (dp[2]+=dp[0])%=mod;
            (dp[0]+=dp[1])%=mod;
            (dp[3]+=dp[1])%=mod;
            dp[1]=0;
        }
        else if(tot)
        {
            if(s[tot--]=='L') ++dp[1];
            else ++dp[2];
        }
    }
    ll ans=((dp[0]+dp[1])%mod+(dp[2]+dp[3])%mod)%mod;
    printf("%lld\n",ans);
    return 0;
}

---

2018.8.17([数据已删除])