阶段3 1.Mybatis_12.Mybatis注解开发_6 mybatis注解开发一对一的查询配置
新建Account实体类
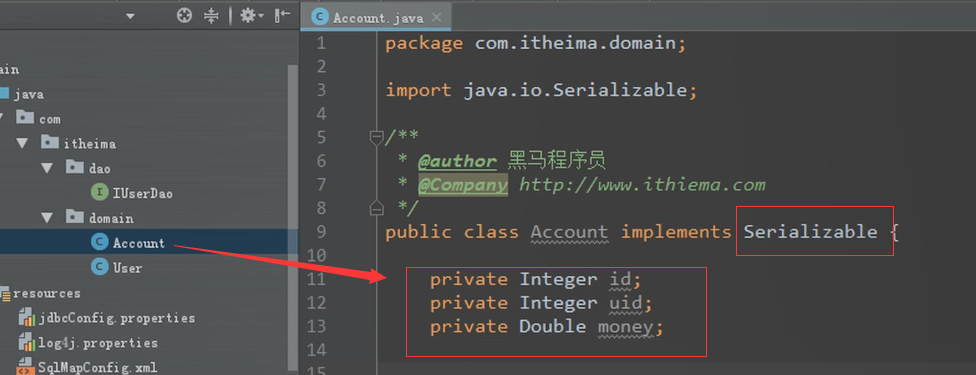
生成getter和setter还有toString方法
先创建dao类
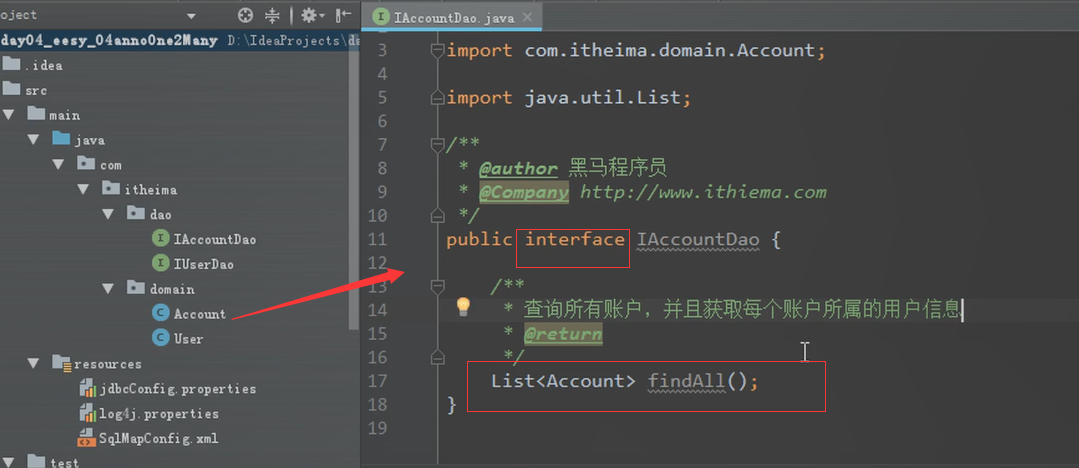
全局的配置,这里要改成package
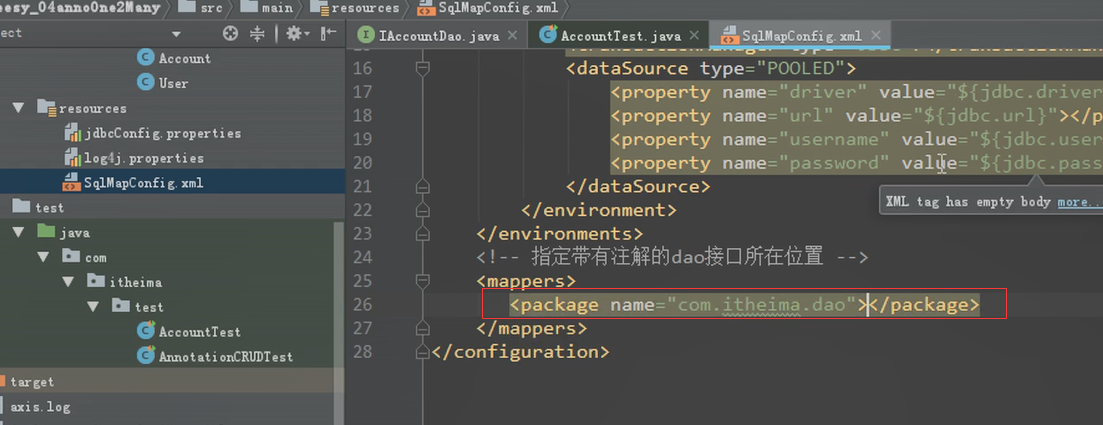
创建多对一的关系
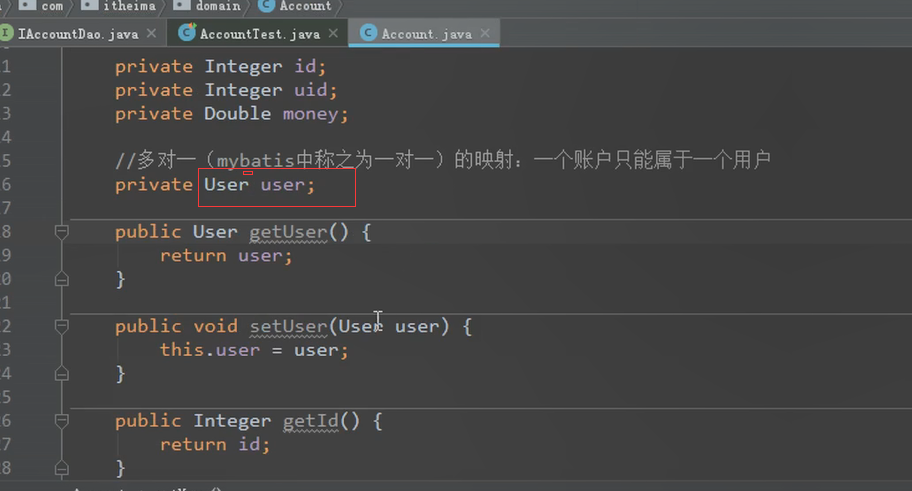
在查询的时候输出user这个对象的内容
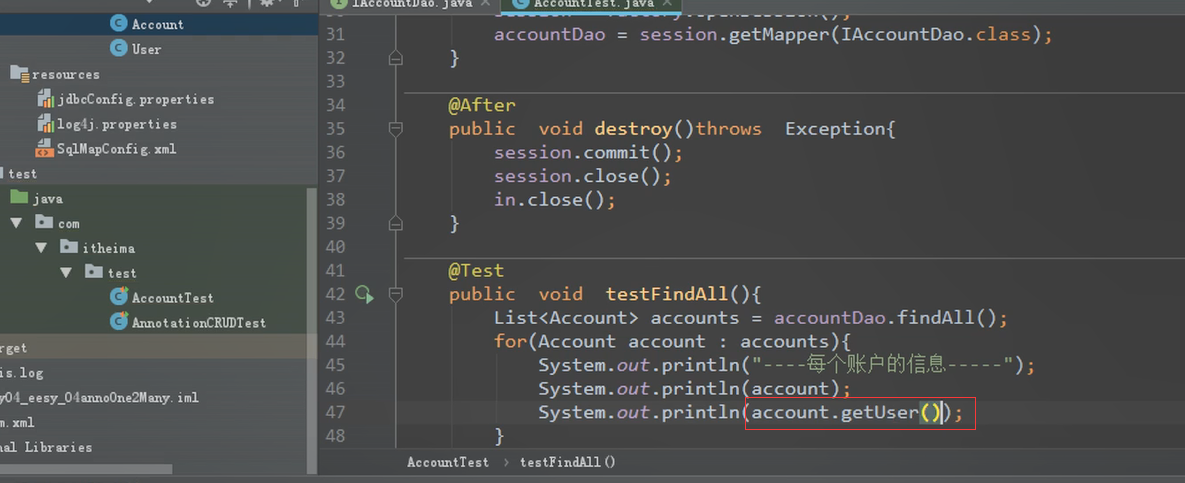
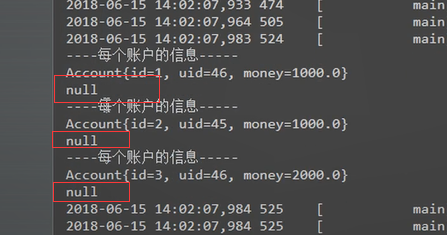
建立查询的映射
account自己的数据封装完了。

result的注解里面还有 one 和 many
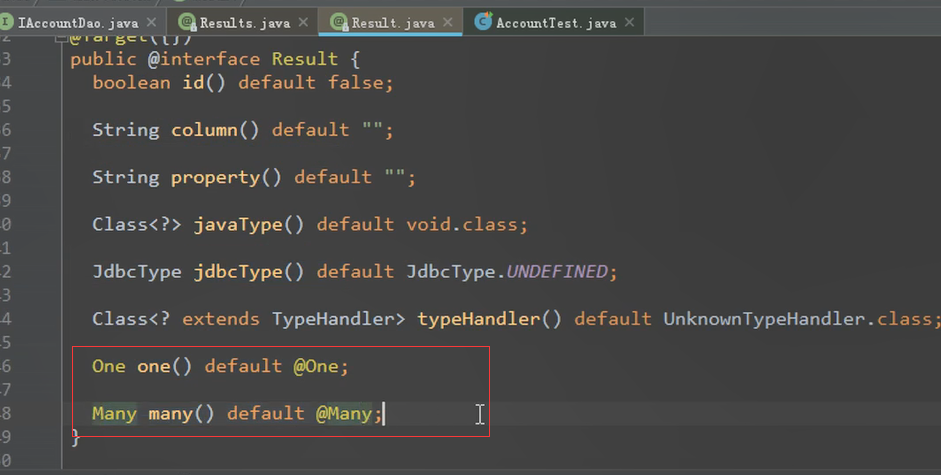
点进去看One对象。select指向的就是如何查询用户的唯一标志
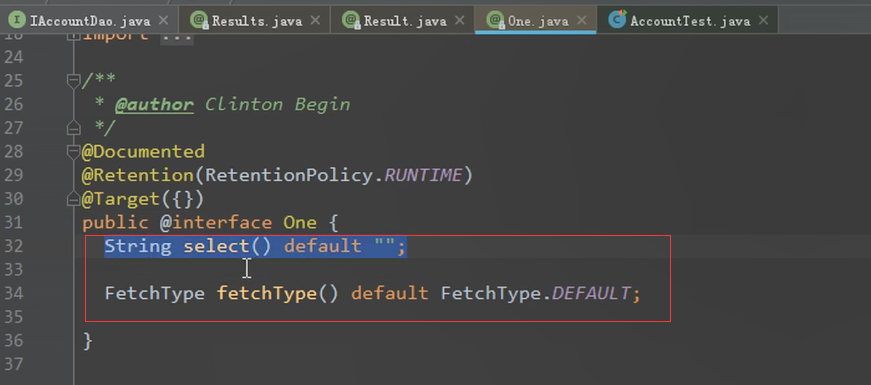
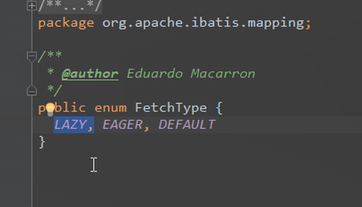
FetechType进去看源码
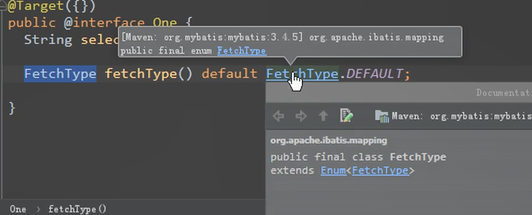
这里有一个lazy延迟加载。eager就是立即加载。实际开开发的时候,对一选择立即加载,对多选择延迟加载。
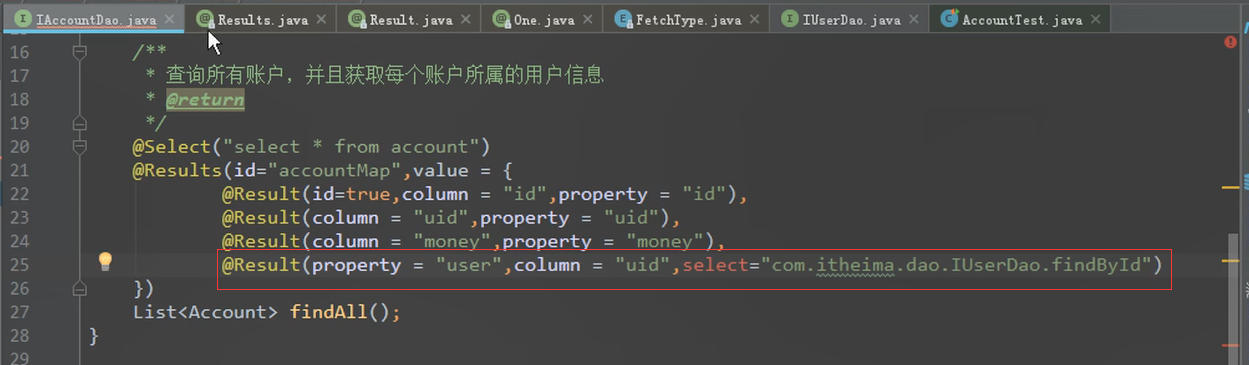
应该把这些属性报在one这个注解里面
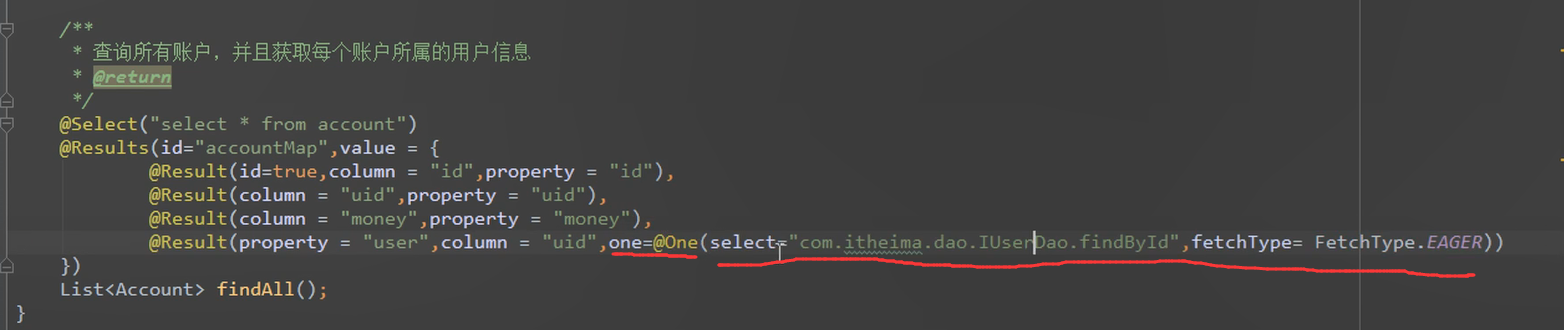
这样一对一的配置就完成了

阶段3 1.Mybatis_12.Mybatis注解开发_6 mybatis注解开发一对一的查询配置的更多相关文章
- MyBatis从入门到放弃三:一对一关联查询
前言 简单来说在mybatis.xml中实现关联查询实在是有些麻烦,正是因为起框架本质是实现orm的半自动化. 那么mybatis实现一对一的关联查询则是使用association属性和resultM ...
- 阶段3 1.Mybatis_06.使用Mybatis完成DAO层的开发_6 Mybatis中使用Dao实现类的执行过程分析-增删改方法
从测试类入手,断点调试 找到实现类,进入到insert方法里面 这里是SqlSession的接口里面的方法. 我们需要找SqlSession的实现类. DefaultSqlSession 里面有两个i ...
- 阶段3 1.Mybatis_11.Mybatis的缓存_6 Mybatis中的一级缓存
Mybatis中的一级缓存和二级缓存 一级缓存: 它指的是Mybatis中SqlSession对象的缓存. 当我们执行查询之后,查询的结 ...
- mybatis学习:mybatis注解开发一对一的查询配置
实体类: public class Account { private Integer id; private Integer uid; private Double money; private U ...
- MyBatis:一对一关联查询
MyBatis从入门到放弃三:一对一关联查询 前言 简单来说在mybatis.xml中实现关联查询实在是有些麻烦,正是因为起框架本质是实现orm的半自动化. 那么mybatis实现一对一的关联查询则是 ...
- Spring+Spring MVC+Mybatis 框架整合开发(半注解半配置文件)
项目结构: (代码里面都有注释) 一.在pom文件中依赖jar包 因为我这里分了模块,所以有父子级的共两个pom文件 父级: <?xml version="1.0" enco ...
- [Spring框架]Spring开发实例: XML+注解.
前言: 本文为自己学习Spring记录所用, 文章内容包括Spring的概述已经简单开发, 主要涉及IOC相关知识, 希望能够对新入门Spring的同学有帮助, 也希望大家一起讨论相关的知识. 一. ...
- spring注解开发中常用注解以及简单配置
一.spring注解开发中常用注解以及简单配置 1.为什么要用注解开发:spring的核心是Ioc容器和Aop,对于传统的Ioc编程来说我们需要在spring的配置文件中邪大量的bean来向sprin ...
- Spring+SpringMVC+MyBatis深入学习及搭建(二)——MyBatis原始Dao开发和mapper代理开发
转载请注明出处:http://www.cnblogs.com/Joanna-Yan/p/6869133.html 前面有写到Spring+SpringMVC+MyBatis深入学习及搭建(一)——My ...
随机推荐
- 为什么现在UML很少用了
新霸哥发现UML在面向对象的设计中的需求,相关行为.一些体系结构的实现提供了一套综合完整的表示法,但是由于使用的人比较少,初学者不容易快速入门,所以就导致了UML不是那么的受欢迎. UML在开发中有什 ...
- VMware 问题
桥接模式下,小鸡上不了网问题 多网卡导致的问题 解决:编辑-虚拟网络编辑器 选择vmnet0,然后点击右下角更改设置 把自动改为指定要桥接的网卡,然后点击确定,测试看看.
- 清北学堂提高组突破营游记day6
还有一天就结束了..QWQ 好快啊. 昨天没讲完的博弈论DP: 一个标准的博弈论dp,一般问的是是否先手赢. 博弈论最关键的问题:dp过程. 对于一个问题,一定有很多状态,每个状态可以转移到其他的一些 ...
- (极值点偏移问题的几种方案)已知$\dfrac{\ln x_1}{x_1}=\dfrac{\ln x_2}{x_2}$,求证:$x_1+x_2>2\text{e}$.
第一个图适合在手机上操作(点击\(\checkmark\)显示/隐藏) 第二个图适合在电脑上操作(点击\(\checkmark\)显示/隐藏)
- 【洛谷P1417】烹调方案 贪心+背包dp
题目大意:一共有 n 件食材,每件食材有三个属性,ai,bi和ci,如果在t时刻完成第i样食材则得到ai-t*bi的美味指数,用第i件食材做饭要花去ci的时间.众所周知,gw的厨艺不怎么样,所以他需要 ...
- 在CentOS 6.4上安装Puppet配置管理工具
在CentOS 6.4上安装Puppet配置管理工具 linux, puppetAdd comments 五052013 上篇说了下在ubuntu12.04上安装puppet,安装的版本为puppet ...
- Python 3标准库课件
开课前的一些讲话: 一.大家晚上好,首先非常的荣幸能够在网易云平台开设讲解Python的这门课程,我也是第一次讲解哦,下面说说我讲解课程的原因,1.因为我发现市场上讲解Python的课程很多,不过,大 ...
- shell练习--关于二维数组的实现问题
关于二维数组的实现问题:通过查询网友们的记录,可知有两个方法 方法1:通过通过2次读取赋值,来获取二维数组的方法. a=('1 2 3' '4 5 6' '7 8 9') for i in " ...
- python中的文件读取
---恢复内容开始--- r模式,只读模式,不可写入,文件不存在会报错 #r模式,能读不能写,文件不存在会报错 f = open('a1.txt')#不写'r',默认只读 result = f.rea ...
- z-tree的使用
1.参考资料 1)官网:http://www.treejs.cn/v3/api.php 2)z-tree码云:https://gitee.com/zTree/zTree_v3 2.下载解压 案例演示: ...
