Python:n个点的费马问题
问题描述
在平面内有n(n>=3)个点N1(x1,y1),N2(x2,y2),...,Nn(xn,yn),现求一点P(x,y),使得P到各点直线距离之和最小。
算法分析
当n=3时,这是著名的三角形费马点问题,网上有详细介绍和证明。
然而,那些平面几何证明看似巧妙,但真正涉及到了n个点的时候,就只能呵呵了,还是得用解析法来想办法。
目标函数为:
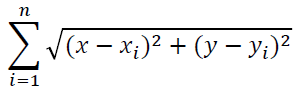
我们需要求它的最小值。
分别对x和y求偏导数:
fx(x,y) = =0
=0
fy(x,y) =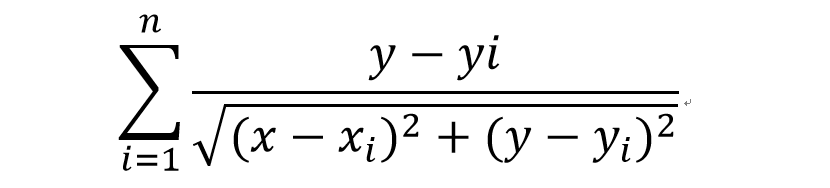 =0
=0
当两偏导数同为0的时候,是此二元函数的驻点。
这里,若再求一次偏导数(二阶偏导数):
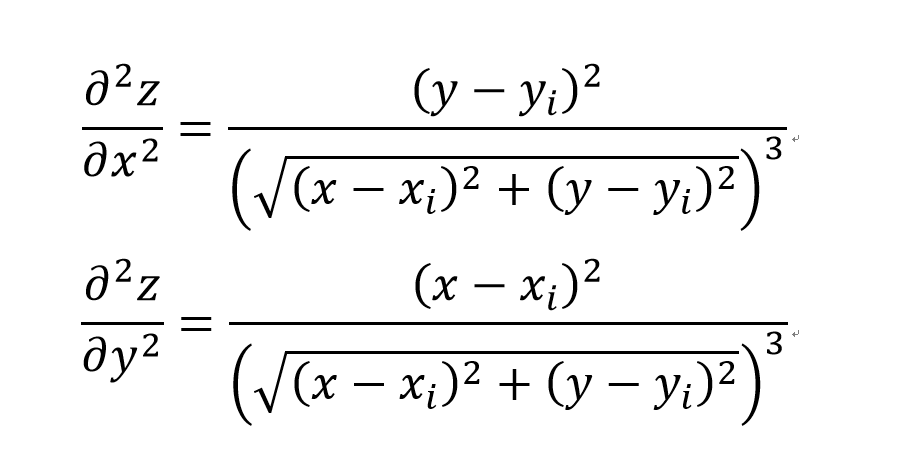
发现其恒大于0,即原函数是个凸函数,一阶偏导数为0的点就是它的最小值点。
那么上面这俩方程(一阶偏导数为0)怎么解呢?
这里就要隆重推出:迭代法。
说句题外话,我们用通俗的说法来辨析几个词:循环、迭代、递归、遍历。我们常常把它们混用,但它们其实是互不相同的!
循环Repeating:反复执行一段程序代码。例如:while循环、for循环...
迭代Iteration:每一次的运算结果会成为下一次运算的初始值,经常用此方法以不断逼近目标结果。例如:牛顿迭代法、二分法、斐波那契数列...
递归Recursion:(函数等)自己调用自己。例如:汉诺塔问题、斐波那契数列...
遍历Traversal:访问一个树的所有结点,每个只访问一次。例如:广度优先搜索、深度优先搜索...
可以看出,有些问题可能会同时涉及到这四个中的多个(其实也不难理解),这大概就是我们常常混淆这四个词的一大原因吧。比如,实现后三者的程序,写代码时基本都跑不掉循环结构,很多人从此就开始混淆它们了...而其实,很多时候它们的思想也是相通的,因此造成了一个问题既可以用迭代也可以用递归的现象,这很正常。
回到本文的问题。我们尝试解一个方程f(x)=0,如果能找到一个g(x)=f(x)+x,从而将原方程转化为x=g(x).通过不断迭代:g(g(g(g(g(x))))),逼近解x。
这其实就是高中数学(一般在竞赛中出现,或是十多年前的很难的高考数学的数列题里出现)里的“不动点”问题。
一个经典的例子就是利用cos(cos(cos(0)))解方程cos(x)=x。利用作图能清晰的看出:

当然了,此种方法对g(x)的图形和x的初始值是有要求的,不然有可能不但不逼近,反而跑的越来越远了。
例如,对于方程3^x-7=x,我们直观的感觉它有两个解,运行如下代码,轻松得到了一个解-6.9995。
import math
m=0
for i in range(10):
m=3**m-7
print(m)
可另外一个解呢?此种方法就很难求了,因为一旦迭代就离它越来越远了。我们尝试更改初始值如m=7来求那个正数的解:
根本执行不了。其实在草稿纸上画画图就能发现,想得到那个解,通过我们这种方法根本不能收敛。
不扯远了,再次回到本题,将x和y可以表示为:
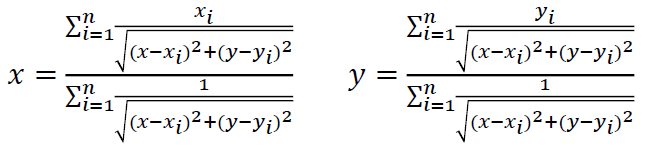
初始值可设为那n个点的重心,其实,最终答案一般都不会离重心太远。
至于为什么本题就可以收敛?由二阶导数>0恒成立知,一阶导数单调,故上述方程仅有一个根。
我们可以作图看看右边这个奇怪的函数和函数f(x)=x的交点,运行以下代码:
import math
import random
import matplotlib.pyplot as plt a1=[];a2=[]
for i in range(6):
a1.append(random.random())
a2.append(random.random()) for j in range(1000):
x=j/1000;y=j/1000
xfenzi=0;xfenmu=0;yfenzi=0;yfenmu=0
for i in range(6):
g=math.sqrt((x-a1[i])**2+(y-a2[i])**2)
xfenzi=xfenzi+a1[i]/g
xfenmu=xfenmu+1/g
yfenzi=yfenzi+a2[i]/g
yfenmu=yfenmu+1/g
xn=xfenzi/xfenmu
yn=yfenzi/yfenmu
plt.scatter(x,xn,color='b',s=1)
plt.scatter(x,x,color='g',s=1) plt.show()
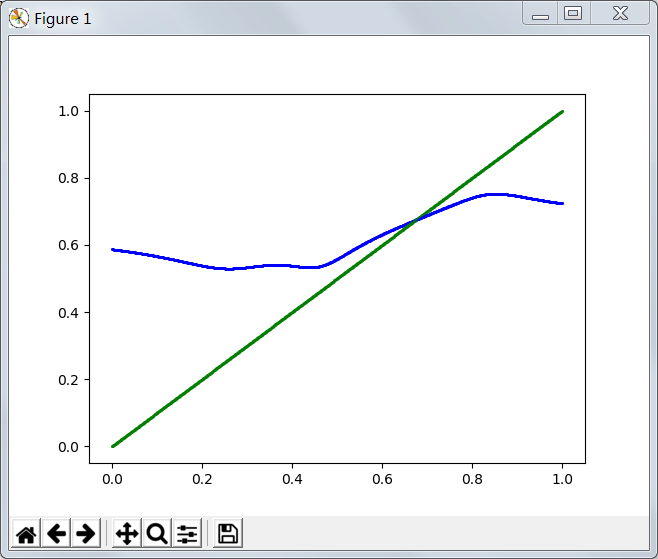
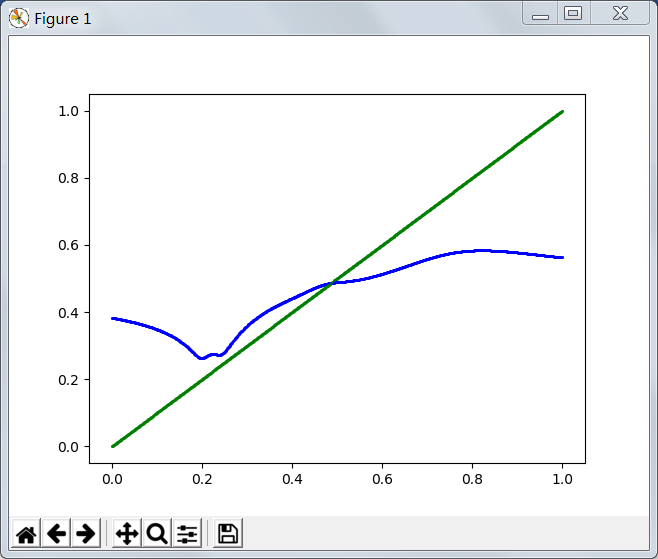
由上述,显然,不论怎么运行,仍是只有一个根。而且很明显这个图形是符合我们描述的那个迭代的,即:通过迭代能逐渐逼近那个交点。
因此,我们可以用迭代法实现找出平面上到n个点距离之和的最小值的费马点了。
以下是Python实现代码:
import math
import random
import matplotlib.pyplot as plt n=int(input('请输入n:'))
a1=[];a2=[]
for i in range(n):
a1.append(random.random())
a2.append(random.random())
plt.scatter(a1,a2,color='r') x=sum(a1)/n;y=sum(a2)/n
while True:
xfenzi=0;xfenmu=0;yfenzi=0;yfenmu=0
for i in range(n):
g=math.sqrt((x-a1[i])**2+(y-a2[i])**2)
xfenzi=xfenzi+a1[i]/g
xfenmu=xfenmu+1/g
yfenzi=yfenzi+a2[i]/g
yfenmu=yfenmu+1/g
xn=xfenzi/xfenmu
yn=yfenzi/yfenmu
if abs(xn-x)<0.01 and abs(yn-y)<0.01:
break
else:
x=xn
y=yn plt.scatter(x,y,color='b')
plt.show()
运行效果:
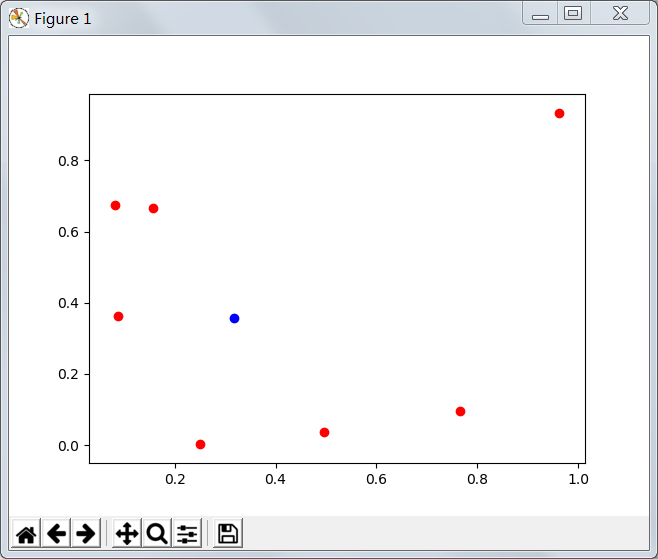
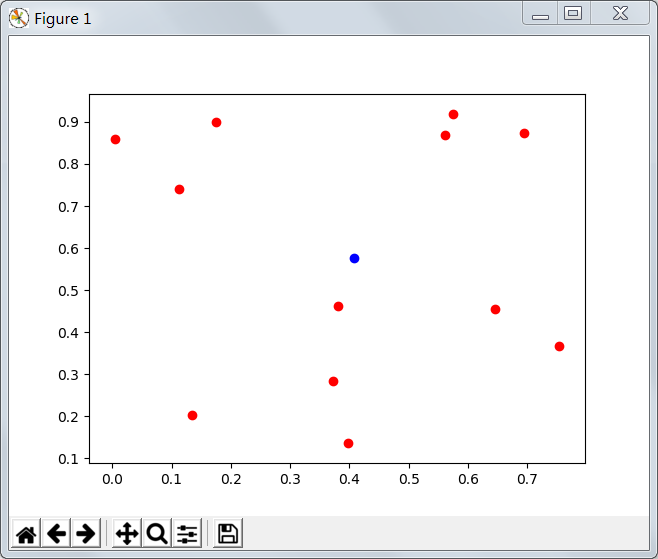
Python:n个点的费马问题的更多相关文章
- 读 CSI讲义 费马小定理
费马小定理 最近在上计算机安全学选修课.. 读老师博客..现在当是写阅读笔记吧. 这里贴出老师的简书建议先看看链接先..毕竟我这些东西只是搞笑一下的.. 遵循一下这个原则… 观察 找规律 求证 首先是 ...
- hdu 4704 Sum (整数和分解+快速幂+费马小定理降幂)
题意: 给n(1<n<),求(s1+s2+s3+...+sn)mod(1e9+7).其中si表示n由i个数相加而成的种数,如n=4,则s1=1,s2=3. ...
- nyoj1000_快速幂_费马小定理
又见斐波那契数列 时间限制:1000 ms | 内存限制:65535 KB 难度:4 描述 斐波那契数列大家应该很熟悉了吧.下面给大家引入一种新的斐波那契数列:M斐波那契数列. M斐波那契数列 ...
- poj 3734 Blocks 快速幂+费马小定理+组合数学
题目链接 题意:有一排砖,可以染红蓝绿黄四种不同的颜色,要求红和绿两种颜色砖的个数都是偶数,问一共有多少种方案,结果对10007取余. 题解:刚看这道题第一感觉是组合数学,正向推了一会还没等推出来队友 ...
- 数论初步(费马小定理) - Happy 2004
Description Consider a positive integer X,and let S be the sum of all positive integer divisors of 2 ...
- 【BZOJ1951】【SDOI2010】古代猪文 Lucas定理、中国剩余定理、exgcd、费马小定理
Description “在那山的那边海的那边有一群小肥猪.他们活泼又聪明,他们调皮又灵敏.他们自由自在生活在那绿色的大草坪,他们善良勇敢相互都关心……” ——选自猪王国民歌 很久很久以前,在山的那边 ...
- 数论 --- 费马小定理 + 快速幂 HDU 4704 Sum
Sum Problem's Link: http://acm.hdu.edu.cn/showproblem.php?pid=4704 Mean: 给定一个大整数N,求1到N中每个数的因式分解个数的 ...
- HDU 5667 Sequence 矩阵快速幂+费马小定理
题目不难懂.式子是一个递推式,并且不难发现f[n]都是a的整数次幂.(f[1]=a0;f[2]=ab;f[3]=ab*f[2]c*f[1]...) 我们先只看指数部分,设h[n]. 则 h[1]=0; ...
- HDU 5793 A Boring Question (逆元+快速幂+费马小定理) ---2016杭电多校联合第六场
A Boring Question Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others ...
随机推荐
- webdriervAPI(WebElement接口常用方法)
from selenium import webdriver driver = webdriver.Chorme() driver.get("http://www.baidu.co ...
- 2019牛客暑期多校训练营(第一场)-B.Integration()
链接:https://ac.nowcoder.com/acm/contest/881/B 题意:给出n,和数组a[n],求特定表达式取模后的值. 思路:用到列项相消:
- [转帖]$PWD 和 $(pwd)
$PWD 和 $(pwd) https://blog.csdn.net/shaojwa/article/details/51894980 细节决定成败. 注意两个效果一样,但是注意大小写,PWD是 ...
- Linux学习笔记(16)Linux前后台进程切换(fg/bg/jobs/ctrl+z)
关键词:Linux前后台进程切换,linux进程切换 fg.bg.jobs.&.ctrl + z都是跟系统任务有关的,虽然现在基本上不怎么需要用到这些命令,但学会了也是很实用的一.& ...
- 跨 PostgreSQL 大版本复制怎么做?| 逻辑复制
当需要升级PostgreSQL时,可以使用多种方法.为了避免应用程序停机,不是所有升级postgres的方法都适合,如果避免停机是必须的,那么可以考虑使用复制作为升级方法,并且根据方案,可以选择使用逻 ...
- 使用idea关联mysql时报错Server returns invalid timezone. Go to 'Advanced' tab and set 'serverTimezon'
版权声明:本文为博主原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明. 本文链接:https://blog.csdn.net/liuqiker/article/detai ...
- DFS搜索算法--(1)基础图遍历 绝对看!的!懂!
内容总结 自<啊哈!算法!> 作为一个都大二的了一个菜鸡,做题的时候DFS怎么可以不会呢!!! 作为一个都大二了的(!!!)菜鸡....<啊哈算法>这本书第四章的搜索,开始那里 ...
- Django 中事务的使用
目录 Django 中事务的使用 Django默认的事务行为 在HTTP请求上加事务 在View中实现事务控制 使用装饰器 使用context manager autocommit() commit_ ...
- LeetCode题解: LRU Cache 缓存设计
LeetCode题解: LRU Cache 缓存设计 2014年12月10日 08:54:16 邴越 阅读数 1101更多 分类专栏: LeetCode 版权声明:本文为博主原创文章,遵循CC 4 ...
- 关于解决SpringDataJpa框架实体类表字段创建顺序与数据库表字段展示顺序不一致的问题
今天在公司的项目开发中,遇到一个问题: 后端对象实体类中写入字段顺序与数据库中的存储顺序不一致. 仔细观察到数据库中的表字段的排序方式是按照拼音字母的顺序abcdef......来存储的 而我的实体类 ...
