【BZOJ1801】【DTOJ2004】 [Ahoi2009]chess 中国象棋 【DP】

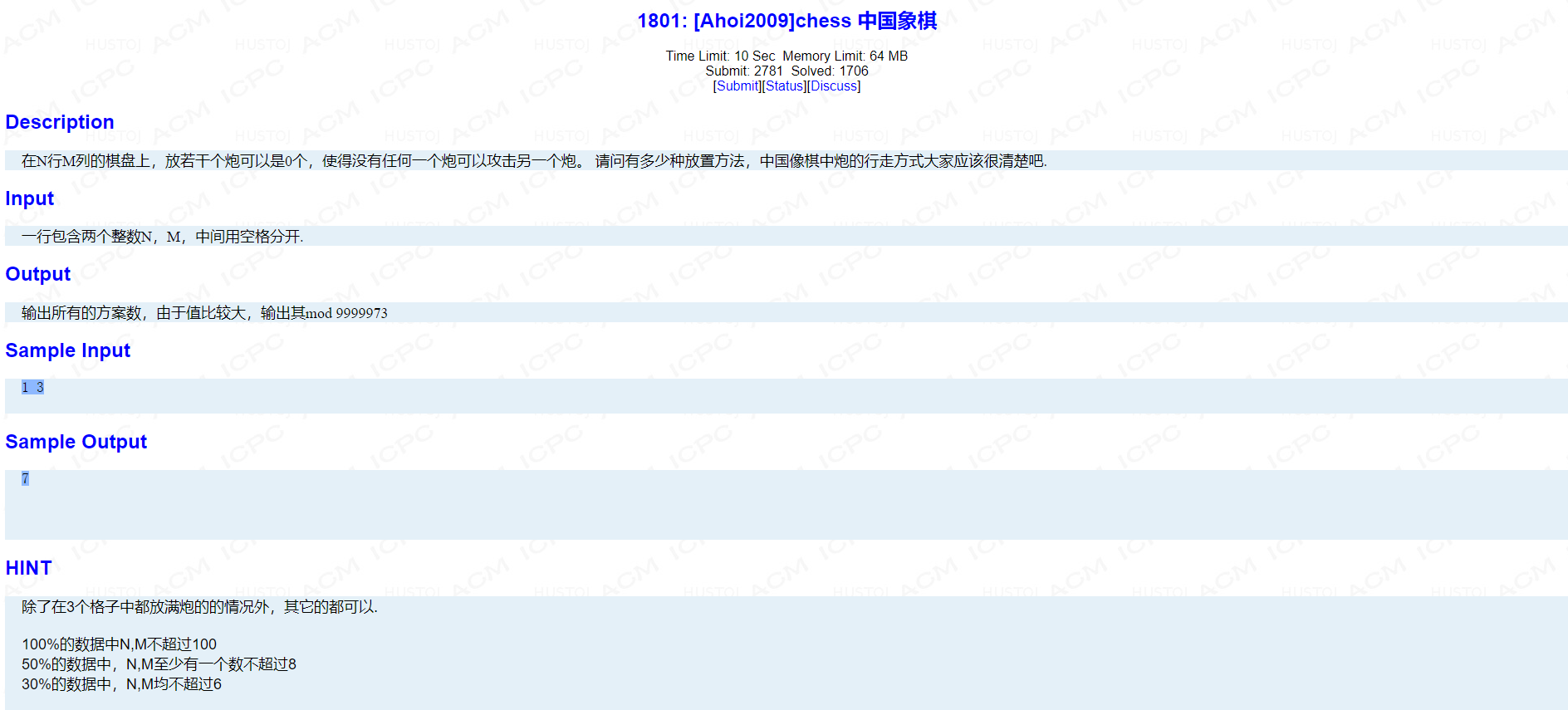
题解：

首先知道一个性质，每一行每一列都最多有两个炮

那么很显然是DP

设F[i][j][k]表示前i行，有j列有一个炮，有k列有两个炮，那么转移式子为

这一行什么都不做：f[i][j][k]=f[i-1][j][k]
这一行填一个炮在列为0：f[i][j][k]=f[i-1][j-1][k]*c(m-j-k+1,1)
这一行填一个炮在列为1：f[i][j][k]=f[i-1][j+1][k-1]*c(j+1,1)
这一行填两个炮在列为0：f[i][j][k]=f[i-1][j-2][k]*c(m-j-k+2,2)
这一行填一个炮在列为0一个炮在列为1：f[i][j][k]=f[i-1][j][k-1]*c(j,1)*c(m-j-k+1,1)
这一行填两个炮在列为1：f[i][j][k]=f[i-1][j+2][k-2]*c(j+2,2)

代码：

#include<iostream>
#include<cstdio>
#include<cstdlib>
#define mod 9999973
#define ll long long
using namespace std;
int n,m,ans;
int f[][][],c[][];
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=;i<=;i++)c[i][]=;
    for(int i=;i<=;i++)
      for(int j=;j<=i;j++)c[i][j]=(c[i-][j-]+c[i-][j])%mod;
    f[][][]=;
    for(int i=;i<=n;i++)
      for(int j=;j<=m;j++)
          for(int k=;j+k<=m;k++)
          {
            f[i][j][k]=f[i-][j][k];
            if(j>=)f[i][j][k]=(f[i][j][k]+(ll)f[i-][j-][k]*c[m-j-k+][]%mod)%mod;
            if(k>= && j+<=m)f[i][j][k]=(f[i][j][k]+(ll)f[i-][j+][k-]*c[j+][]%mod)%mod;
          if(j>=)f[i][j][k]=(f[i][j][k]+(ll)f[i-][j-][k]*c[m-j-k+][]%mod)%mod;
          if(j>= && k>=)f[i][j][k]=(f[i][j][k]+(ll)f[i-][j][k-]*c[j][]%mod*c[m-j-k+][]%mod)%mod;
          if(k>= && j+<=m)f[i][j][k]=(f[i][j][k]+(ll)f[i-][j+][k-]*c[j+][])%mod;
        }
    for(int i=;i<=m;i++)
      for(int j=;j<=m;j++)ans=(ans+f[n][i][j])%mod;
    return !printf("%d\n",ans);
}