平衡树splay学习笔记#1

这一篇博客只讲splay的前一部分的操作（rotate和splay），后面的一段博客咕咕一段时间

后一半的博客地址：【传送门】

前言骚话

为了学lct我也是拼了，看了十几篇博客，学了将近有一周，才A掉模板题和文艺平衡树。
这一片博客就是写了跟我之前有相同处境的小伙伴们。我尽可能的写的简单一点，在带一点自己学习时候的心得和总结。（难免会有一点冗长，大佬勿喷）
吐槽：splay=cosplay=slay（滑稽）
如要转载，请注明出处和作者：https://www.cnblogs.com/chhokmah/p/10577166.html 。作者chhokmah（扒我的图片的时候要和我说一声，不要把水印删掉了，不要吐槽我的图非常丑陋QwQ）。

简要介绍一下splay

splay（伸展树）是一种二叉搜索树。所谓二叉搜索树，又称作二叉查找树，二叉排序树。
二叉搜索树具有以下的性质：如果左树非空，那么左树中所有的节点所代表的权值都小于根节点的权值。同理右子树中所有节点所代表的权值都大于根节点的权值。和二分查找非常的相似，没错就是参照了二分的思路实现了这种数据结构。（话说二分真的好厉害呀QwQ）。
以下这个图片上显示的就是一棵简单的二叉搜索树，接下来我们都用BST（Binary Search Tree）来简写二叉搜索树。

但是还有一个非常极端的情况，请看下图：

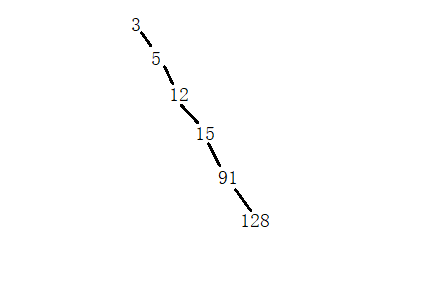
上图描述就是所有树形结构都必须要解决的共同问题，退化成一条链，虽然还是保持的是BST的性质，但是我们查询的复杂度就会变成了\(O(n)\)，那么很多BST的操作都可以解决这个问题，比如说treap的随机标记，还有我们今天要讲的splay伸展操作。

---

话说这东西又是tarjan大佬做出来的，太强了。
来自百度百科的描述：它由丹尼尔·斯立特Daniel Sleator 和 罗伯特·恩卓·塔扬Robert Endre Tarjan 在1985年发明的。%%% orz。

---

update 2019/3/23
感觉还是要明确一下splay的结构体

struct node {
    int val, fa, cnt, sz, ch[2];
    void init(int x, int ft) {
        fa = ft;
        val = x;
        ch[1] = ch[0] = 0;
        sz = cnt = 1;
    }
}

分别解释一下，val表示的是当前节点代表的权值，fa表示这个节点的父亲节点，cnt表示有多少相同的权值，因为在BST中不存在相同的节点，那么就需要把相同的权值都放到相同的节点内，ch[0]和ch[1]分别表示左儿子和右儿子。

---

Q：为什么很多BST要有旋转（rotate）操作？
A：为了防止出现链的情况，我们需要在保证BST原来的性质的条件下，将BST的结构改掉，这样就不会有链的情况了。
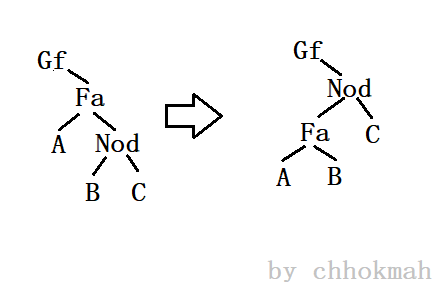
比如说看一下下面这种图片：（给出的样例是Nod是父亲的左儿子，Fa为祖父的左儿子）

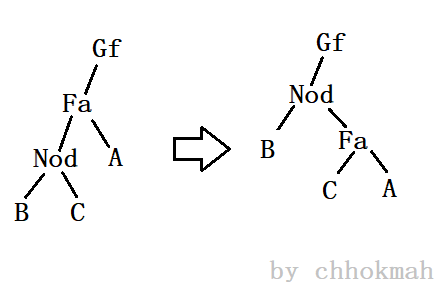
天哪我放的有一点快了，但是不影响阅读。我们就将上图左图当做我们现在的BST。
根据BST的性质，容易得出Gf>A>Fa>C>Nod>B。为了改造BST的结构，那么我们就考虑将Nod（当前节点）旋转到父亲节点Fa的位置。
Nod和他的Fa的关系是Nod<Fa，那么如果要让Nod做Fa的父亲的位置，那么Fa一定是Nod的右节点。
因为Fa变成了Nod的一个子节点，那么Gf（祖父节点）的左儿子就变成了Nod节点，说的普遍一点，就是Nod代替了原来自己父亲的位置（大义灭亲）。
再回到Nod原来的子节点，因为维护二叉的性质，那么我们需要让Nod的其中一个儿子变成Fa的儿子。
我们选择了C号节点，因为原来的Nod节点的有儿子就是C节点，而现在被Fa代替掉了。因为C是Nod的子节点，那么C<Fa，因此，C号节点就变成了Fa的左节点，那么原来的B号节点就不需要移动了。
旋转之后得到的就是上面图片的右图，重新审核一下我们图的大小关系。Gf>A>Fa>C>Nod>B，和原来的树是一样的顺序，而且也将原来的那个链的结构改掉了，维护了BST的复杂度。完美؏؏☝ᖗ乛◡乛ᖘ☝؏؏。
还有更多的旋转的情况，以下三种大家可以推一下对照一下是不是这样的：
情况二：Nod是父亲的右节点，Fa是Gf的左节点

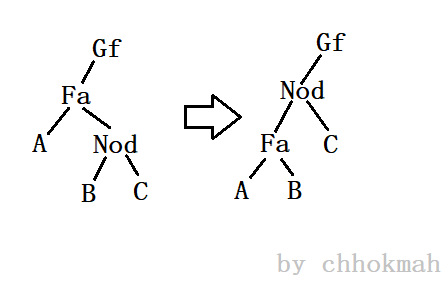
情况三：Nod是父亲的左节点，Fa是Gf的右节点

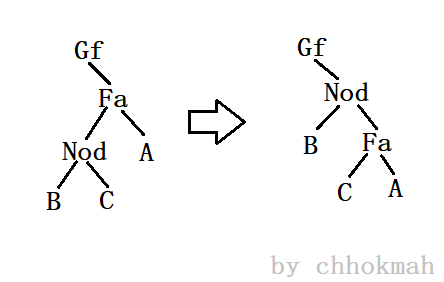
情况四：Nod是父亲的右节点，Fa是Gf的右节点

---

作为一个合格oier，代码还是需要写的。我们先整理一下rotate旋转操作的思路吧。
先针对nod节点，我们可以发现nod节点在每一幅图中都有一个节点是不变的，反观我们之前推导的Fa变成nod节点的其中一个子节点可得，nod是fa的哪一个节点，那么nod的哪一个节点就不会改变。另外一个节点就变成了fa的另一个节点。
那么nod节点本身就会变成Gf的一个子节点。
总结一下过程：
1.nod变到原来fa的位置
2.fa变成了 nod原来在fa的 相对的那个儿子
3.fa的非nod的儿子不变 nod的 nod原来在fa的 那个儿子不变
4.nod的 nod原来在fa的 相对的 那个儿子 变成了 fa原来是nod的那个儿子。

给出代码

void rotate(int nod) {
        int fa = tr[nod].fa, gf = tr[fa].fa, k = tr[fa].ch[1] == nod;//fa和gf都是上面提到的意思
        tr[gf].ch[tr[gf].ch[1] == fa] = nod;//先把fa原来的位置变成nod
        tr[nod].fa = gf;//更新父亲
        tr[fa].ch[k] = tr[nod].ch[k ^ 1];//nod的与nod原来在fa的相对的那个儿子变成fa的儿子
        tr[tr[nod].ch[k ^ 1]].fa = fa;//更新父亲
        tr[nod].ch[k ^ 1] = fa;//nod的 与nod原来相对位置的儿子变成 fa
        tr[fa].fa = nod;//更新父亲
    }

---

接下来就是splay操作，沃觉得splay操作有两个用处：

• 将某一个节点提到某一个位置
• 维护树的复杂度，这个复杂度指的是查询等其他操作时的时间复杂度。

我们思考一个问题，如果我们需要把一个节点提到某一个需要的位置，也许就是根节点，需要怎么操作。
第一次我想到的就是，不断向上旋转，但是这样是错误的，会T到爆炸。
请看一下下面的图：（这个图实在是太丑了）

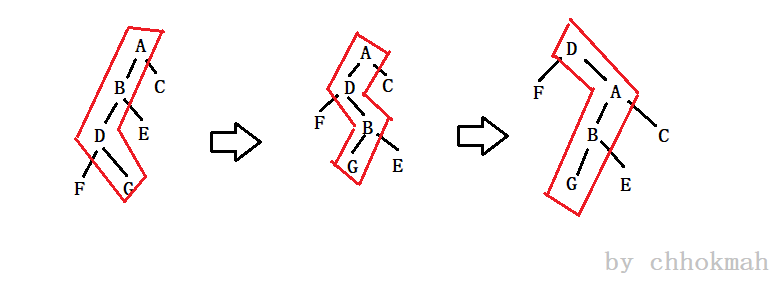
还有一个动态图

把一个点双旋到根，可以使得从根到它的路径上的所有点的深度变为大约原来的一半，其它点的深度最多增加2
很明显，我们旋转过后，虽然节点编号之间的顺序发生了变化，但是这条链还依旧是存在的，动态图中更加明显。
为了解决这个问题，我们需要修改一下splay操作，加入判断是否儿子节点是否相同。

• nod和fa分别是fa和gf的同一个儿子
• nod和fa不是fa和gf的同一个儿子

那么对于第一种操作就是先旋转fa，在旋转nod
第二种操作是旋转两遍nod。

代码说话

void splay(int nod, int goal) {//goal表目标节点
    while (tr[nod].fa != goal) {
        int fa = tr[nod].fa, gf = tr[fa].fa;
        if (gf != goal) {
            if ((tr[gf].ch[0] == fa) ^ (tr[fa].ch[0] == nod)) rotate(nod);
            else rotate(fa);
        }
        rotate(nod);//再次旋转
    }
    if (goal == 0) rt = nod;//如果目标节点是0，那么就把根节点变成nod节点
}