「NOIP2000」「Codevs1042」 进制转换

题目描述 Description

我们可以用这样的方式来表示一个十进制数： 将每个阿拉伯数字乘以一个以该数字所处位置的（值减１）为指数，以１０为底数的幂之和的形式。例如：１２３可表示为 １＊１０^２＋２＊１０^１＋３＊１０^０这样的形式。

与之相似的，对二进制数来说，也可表示成每个二进制数码乘以一个以该数字所处位置的（值－１）为指数，以２为底数的幂之和的形式。一般说来，任何一个正整数Ｒ或一个负整数－Ｒ都可以被选来作为一个数制系统的基数。如果是以Ｒ或－Ｒ为基数，则需要用到的数码为 ０，１，．．．．Ｒ－１。例如，当Ｒ＝７时，所需用到的数码是０，１，２，３，４，５和６，这与其是Ｒ或－Ｒ无关。如果作为基数的数绝对值超过１０，则为了表示这些数码，通常使用英文字母来表示那些大于９的数码。例如对１６进制数来说，用Ａ表示１０，用Ｂ表示１１，用Ｃ表示１２，用Ｄ表示１３，用Ｅ表示１４，用Ｆ表示１５。

在负进制数中是用－Ｒ 作为基数，例如－１５（十进制）相当于１１０００１（－２进制），并且它可以被表示为２的幂级数的和数：

１１０００１＝１＊（－２）^５＋１＊（－２）^４＋０＊（－２）^３＋０＊（－２）^２＋

０＊（－２）^１ ＋１＊（－２）^０

    设计一个程序，读入一个十进制数和一个负进制数的基数, 并将此十进制数转换为此负进制下的数：     －Ｒ∈｛－２，－３，－４，．．．，－２０｝　

输入描述 Input Description

输入的每行有两个输入数据。

第一个是十进制数Ｎ（－32768＜＝Ｎ＜＝32767）；  第二个是负进制数的基数－Ｒ。

输出描述 Output Description

结果显示在屏幕上，相对于输入，应输出此负进制数及其基数，若此基数超过１０，则参照１６进制的方式处理。

样例输入 Sample Input

30000 -2

-20000 -2

28800 -16

-25000 -16

样例输出 Sample Output

30000=11011010101110000(base-2)

-20000=1111011000100000(base-2)

28000=19180(base-16)

-25000=7FB8(base-16)

数据范围及提示 Data Size & Hint

上面已述。

题解

啊真是好久没发博客了（懒腰

其实这道题就是把一个十进制数转成某个负进制。我们肯定学过正进制数转换，所以考虑如何把正进制转换的方法迁移过来。

其实是一样的鸭，也是短除法

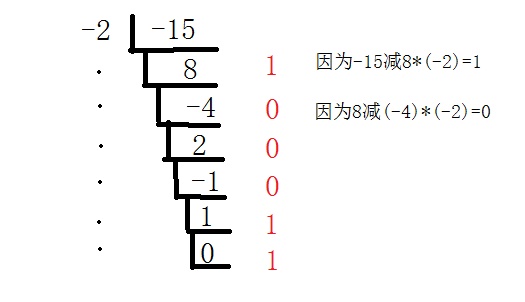
eg:-15(10)=110001(-2)

(图是毛来的)

把n%r的余数作为这一位的值，然后把n/=r，直到n==0

而与正进制的一丢丢区别就是，蠢萌的计算机算负数取余的值可能会给出负数（eg:（-15）%（-2）=（-1）），所以强行把原商+1，把余数转成正数就好啦（撒花

 #include<cstdio>
 #include<iostream>
 using namespace std;
 char a[]={'','','','','','','','','','','A','B','C','D','E','F','G','H','I'};
 int ans[];
 int toa=;
 int main()
 {
     int n,r;
     scanf("%d%d",&n,&r);
     printf("%d=",n);
     while(n)
     {
         if(n<&&n%r!=)
         {
             ans[++toa]=n-((n/r)+)*r;
             //cout<<n<<" "<<n/r+1<<" "<<r<<endl;
             n=n/r+;
         }
         else
         {
             ans[++toa]=n%r;
             //cout<<n<<" "<<r<<endl;
             n/=r;
         }
     }
     while(toa)
     {
         cout<<a[ans[toa]];
         toa--;
     }
     printf("(base%d)",r);
     return ;
 }