hihoCode #1151 : 骨牌覆盖问题·二

#1151 : 骨牌覆盖问题·二

Time Limit:10000ms

Case Time Limit:1000ms

Memory Limit:256MB

描述

上一周我们研究了2xN的骨牌问题，这一周我们不妨加大一下难度，研究一下3xN的骨牌问题？
所以我们的题目是：对于3xN的棋盘，使用1x2的骨牌去覆盖一共有多少种不同的覆盖方法呢？
首先我们可以肯定，奇数长度一定是没有办法覆盖的；对于偶数长度，比如2，4，我们有下面几种覆盖方式：

提示：3xN骨牌覆盖

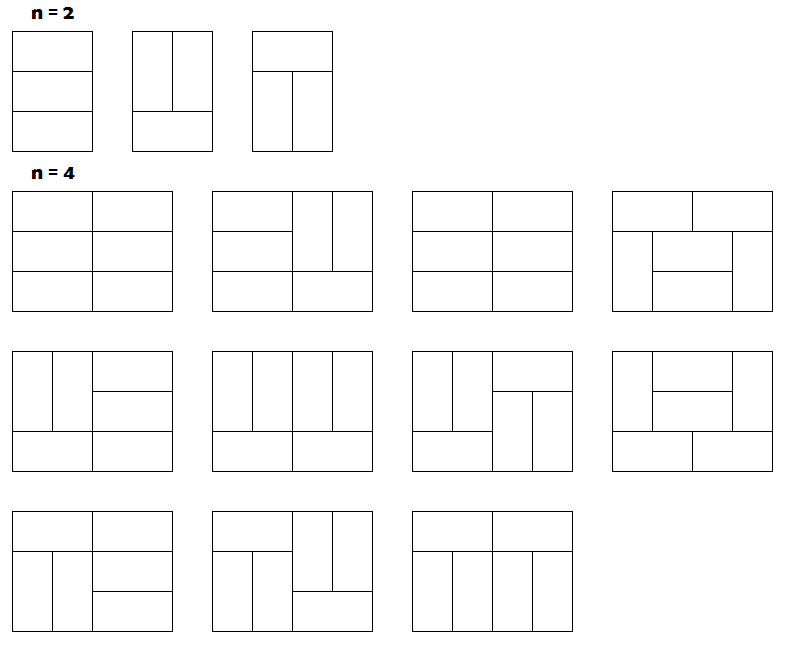
输入

第1行：1个整数N。表示棋盘长度。1≤N≤100,000,000

输出

第1行：1个整数，表示覆盖方案数 MOD 12357

Sample Input

62247088

Sample Output

4037

解题：造转移方程

 #include <bits/stdc++.h>
 using namespace std;
 typedef long long LL;
 const LL mod = ;
 struct Matrix{
     int m[][];
     Matrix(){
         init();
     }
     void init(){
         memset(m,,sizeof m);
     }
     Matrix operator*(const Matrix &rhs){
         Matrix ret;
         for(int k = ; k < ; ++k)
             for(int i = ; i < ; ++i)
                 for(int j = ; j < ; ++j)
                     ret.m[i][j] = (ret.m[i][j] + m[i][k]*rhs.m[k][j])%mod;
         return ret;
     }
     void print(){
         for(int i = ; i < ; ++i){
             for(int j = ; j < ; ++j)
                 printf("%d ",m[i][j]);
             cout<<endl;
         }
     }
 };
 Matrix a,b;
 void quickPow(LL index){
     while(index){
         if(index&) a = a*b;
         index >>= ;
         b = b*b;
     }
 }
 bool tab[][];
 void dfs(int cur,int st){
     if(cur >= ){
         int ss = ;
         for(int i = ; i >= ; --i){
             ss <<= ;
             ss |= tab[i][];
         }
         b.m[st][ss]++;
         return;
     }
     if(!tab[cur][]){
         if(!tab[cur][]){
             tab[cur][] = tab[cur][] = true;
             dfs(cur+,st);
             tab[cur][] = tab[cur][] = false;
         }
         if(cur +  < ){
             if(!tab[cur+][]){
                 tab[cur+][] = tab[cur][] = true;
                 dfs(cur+,st);
                 tab[cur+][] = tab[cur][] = false;
             }
         }
     }else dfs(cur + ,st);
 }
 void init(int st){
     memset(tab,false,sizeof tab);
     for(int i = ,xst = st; i < ; ++i,xst >>= )
         tab[i][] = xst&;
     dfs(,st);
 }
 int main(){
     int n;
     while(~scanf("%d",&n)){
         b.init();
         a.init();
         for(int i = ; i <= ; ++i) init(i);
         a.m[][] = ;
         quickPow(n);
         printf("%d\n",a.m[][]);
     }
     return ;
 }