luoguP1216 [USACO1.5] [IOI1994]数字三角形 Number Triangles

[USACO1.5] [IOI1994]数字三角形 Number Triangles

题目描述

观察下面的数字金字塔。

写一个程序来查找从最高点到底部任意处结束的路径，使路径经过数字的和最大。每一步可以走到左下方的点也可以到达右下方的点。

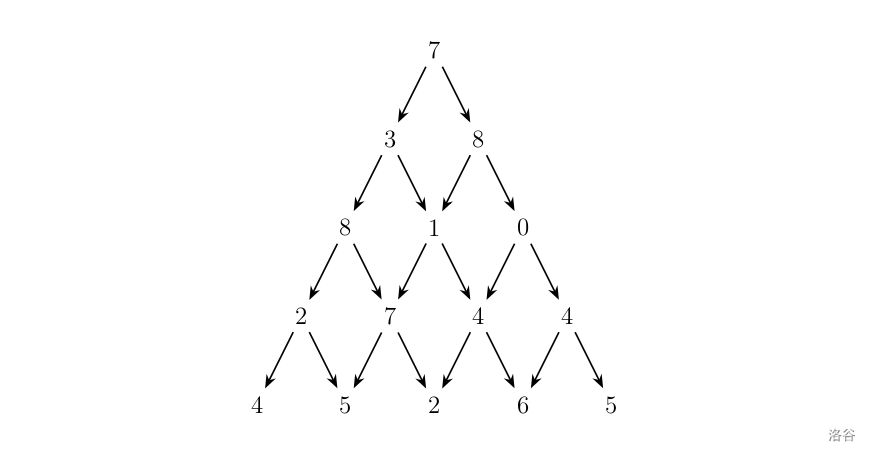
在上面的样例中，从 \(7 \to 3 \to 8 \to 7 \to 5\) 的路径产生了最大权值。

输入格式

第一个行一个正整数 \(r\) ,表示行的数目。

后面每行为这个数字金字塔特定行包含的整数。

输出格式

单独的一行,包含那个可能得到的最大的和。

样例 #1

样例输入 #1

5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5

样例输出 #1

30

提示

【数据范围】

对于 \(100\%\) 的数据，\(1\le r \le 1000\)，所有输入在 \([0,100]\) 范围内。

题目翻译来自NOCOW。

USACO Training Section 1.5

IOI1994 Day1T1

本题思路

抽象出数字三角形的行与列，根据题意发现任意点(i，j)只能由其左上方点i-1，j-1或者右上方点i -1，j加上到当前点这条边而来，由此到达(n，m)点的

关于初始化

copy来了i=1，j=1的写法的初始化，但是我下面的写法是i=0，j=0

for(int i=0;i<=n;++i)
        for(int j=0;j<=i+1;++j)//会找左右上虚拟点，所以每行列多开一个点

ACcode_pull型

#include <iostream>

using namespace std;

const int N = 1010;

int a[N][N];
int n, res;
int dp[N][N];

int main()
{
    //读入数字三角行
    cin >> n;
    for(int i = 0; i < n; ++ i)
        for(int j = 0; j <= i; ++ j) cin >> a[i][j];

    dp[0][0] = a[0][0];

    //自底而上递推
    for(int i = 1; i < n; ++ i)
        for(int j = 0; j <= i; ++ j)
            dp[i][j] = max(dp[i - 1][j - 1] + a[i][j], dp[i -1][j] + a[i][j]);

    //求值
    for(int i = 0; i < n; ++ i)
        res = max(res, dp[n - 1][i]);
    cout << res << endl;
    return 0;
}

本人思路

没有好好的看题，然后只是听课草草了事，大失败，其实超级简单有手就行