卡掉hash的方法

大质数hash

通常，这个质数会选择在 \(10^9\) 附近，如 \(998244353\)，\(10^9+7\)。

考虑生日碰撞，欲达到 50% 成功率，需要尝试的次数为

\[\begin{align}
Q(H)\approx\sqrt{\frac\pi2H}\approx39623
\end{align}
\]

可以参考概率表

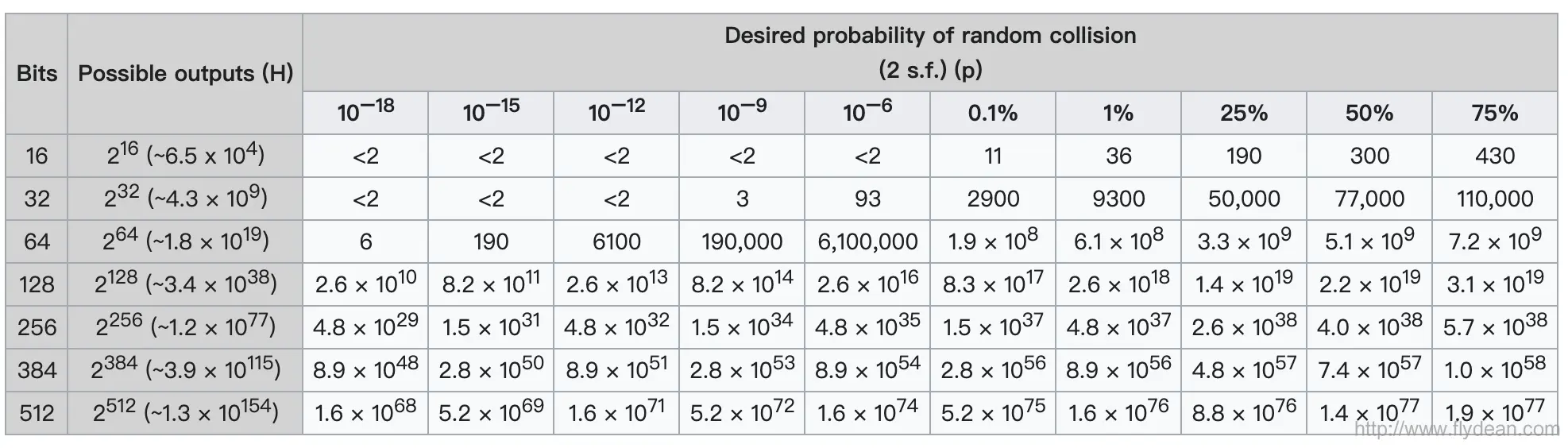
所以我们可以生成 \(10^5\) 左右个较短的字符串，即可有很大的概率发生hash冲突。

Code

#include<iostream>
#include<algorithm>
#include<cstring>
#include<map>
#include<vector>
#include<limits.h>
#define LL long long
#define ULL unsigned long long
using namespace std;

vector<string> create(unsigned num,unsigned int sze)
{
	vector<string>ans;
	while(num--)
	{
		string str;
		for(unsigned int i=0;i<sze;i++)
		{
			str.push_back('a'+rand()%26);
		}
		ans.push_back(str);
	}
	return ans;
}

bool check(vector<string>strs,ULL base,ULL p)
{
//	sort(strs.begin(),strs.end());
	map<int,string>Map;
	for(unsigned int i=0;i<strs.size();i++)
	{
		ULL x=0;
		for(unsigned int j=0;j<strs[i].size();j++)
		{
			x=x*base+strs[i][j]-'a';
			x%=p;
		}
		if(Map.find(x)==Map.end()) Map[x]=strs[i];
		else
		{
			if(Map[x]!=strs[i]) return 1;
		}
	}
	return 0;
}

int main()
{
	srand(time(0));
	int T=100,succ=0;
	for(int t=0;t<T;t++)
	{
		vector<string>strs=create(100000,10); // 生成100000个长度为10的随机字符串
		bool c=check(strs,31,998244853); // base=31,p=998244353，检查是否存在hash冲突
		cout<<c<<endl;
		succ+=c;
	}
	cout<<succ<<"/"<<T<<endl;

	return 0;
}

试运行发现，设置字符串数量为\(39623\)时，发生hash冲突的概率近似\(50\%\)，符合预期。而当设置字符串数量为\(100000\)时，\(1000\)次测试中只有\(4\)次没有发生hash冲突。所以设置\(10^5\)个字符串就差不多可以卡掉绝大多数单大质数hash了。

64位无符号整数自然溢出

首先需要对base奇偶性分类讨论。

当base是偶数时比较简单：设第 \(i\) 位指的是字符串从右往左数第 \(i\) 个字符，设有相同串 \(C\) ，其长度不小于64.构造字符串 \(A=a+C,B=b+C\)，这两个字符串的后64位上均相同，更高位上不相同。

字符串中第 \(i\) 位的权重为 \(base^{i-1}\)，则高于64位上的字符的权重一定可以被 \(2^{64}\) 整除。也就是说，高于64位上的字符不会对hash值产生影响。

下面着重说一下base为奇数的情况。

构造方法

考虑使用字符a和b构造字符串：

记 \(\overline A\) 表示字符串 \(A\) 中所有 a 变成 b ，所有 b 变成 a。

记 \(A_1=a\)，\(A_i=A_{i-1}+\overline{A_{i-1}}\)

例如 \(A_2=ab,A_3=abba,A_4=abbabaab\)

那么\(len(A_i)=2^{i-1}\)

可以证明，当 \(i\) 大于某个数时，\(hash(A_i)=hash(\overline{A_i})\)

证明

由于我们的hash函数使用的是64位无符号整数自然溢出，所以相当于我们需要证明

\[\begin{align}
2^{64}\mid(hash(A_i)-hash(\overline{A_i}))
\end{align}
\]

设\(f(i)=hash(A_i)-hash(\overline{A_i})\)

根据递推公式可得

\[\begin{align}
hash(A_i)&=hash(A_{i-1})\times base^{len(A_{i-1})}+hash(\overline{A_{i-1}})\\
&=hash(A_{i-1})\times base^{2^{i-2}}+hash(\overline{A_{i-1}})
\end{align}
\]

则有

\[\begin{align}
f(i)&=(hash(A_{i-1})-hash(\overline{A_{i-1}}))\times base^{2^{i-2}}+(hash(\overline{A_{i-1}})-hash(A_{i-1}))\\
&=(hash(A_{i-1})-hash(\overline{A_{i-1}}))\times (base^{2^{i-2}}-1)\\
&=f(i-1)\times (base^{2^{i-2}}-1)
\end{align}
\]

设\(g(i)=base^{2^{i-2}}-1(i\ge2)\)

则有

\[\begin{align}
f(i)&=f(i-1)\times g(i)\\
&=f(i-2)\times g(i) \times g(i-1)\\
&=f(1)\times g(i)\times g(i-1)\times g(i-2)\times\dots\times g(2)
\end{align}
\]

由于 \(base\) 是奇数，所以 \(base^{2^{i-2}}\) 也是奇数，故 \(g(i)\) 是偶数。

故有

\[\begin{align}
2^{i-1}\mid f(i)
\end{align}
\]

为了达到\(2^{64}\mid f(i)\)，需取\(i=65\)即可，但是这样会构造两个长度为\(2^{64}\approx10^{20}\)的字符串，是不可行的。

由于\(g(i)=base^{2^{i-2}}-1=(base^{2^{i-3}}+1)(base^{2^{i-3}}-1)=偶数*g(i-1)\)

所以有

\[\begin{align}
2^{i-1} & \mid g(i)\\
2^\frac{i(i-1)}{2} & \mid f(i)
\end{align}
\]

我们需要\(\frac{i(i-1)}{2}\ge64\)，则只需取\(i=12\)，构造出字符串 \(A_{12}\) 和 \(\overline{A_{12}}\)，即可卡掉base为奇数的自然溢出。

最后，在这两字符串后再加上长度大于等于64的相同串，即可同时卡掉base为偶数的自然溢出。

Code

#include<iostream>
#include<string>
#include<cmath>
#include<map>
#include<vector>
#include<limits.h>
#define ULL unsigned long long
using namespace std;

string C;

string create()
{
	string str="a";
	for(int i=2;i<=11;i++) // 会产生长度为2^(i-1)长度的字符串，而我们需要i_max=12
	{
		for(int j=0;j<(1<<(i-2));j++) //延拓字符串长度为1<<(i-1)
		{
			str.push_back(str[j]=='a'?'b':'a');
		}
	}
	return str;
}

string Not(string str)
{
	for(unsigned int i=0;i<str.size();i++)
	{
		str[i]=(str[i]=='a'?'b':'a');
	}
	return str;
}

bool check(string a,string b,ULL base)
{
	ULL aa=0,bb=0;
	for(unsigned int i=0;i<a.size();i++)
	{
		aa=aa*base+a[i]-'a';
	}
	for(unsigned int i=0;i<b.size();i++)
	{
		bb=bb*base+b[i]-'a';
	}
	return aa==bb;
}

int main()
{
	for(int i=1;i<=65;i++) C.push_back('a');
	string str=create();
	string A=str+C,B=Not(str)+C;
	cout<<"构造的字符串的长度为"<<A.size()<<endl;
	int T=10000,succ=0;
	for(int t=0;t<T;t++)
	{
		bool c=check(A,B,t*2+1);
		cout<<c<<endl;
		succ+=c;
	}
	cout<<succ<<"/"<<T<<endl;

	return 0;
}

疑惑：为什么这里取 \(i=11\) 就可以了？

我在研究的过程中，发现取 \(i=11\) 时，对于测试的所有奇数base都成功了。但是明明证明的是 \(i\) 最小取 \(12\)？最后由lzh揭开了谜团。

\(g(3)\) 很特别：\(g(3)=base^{2^{3-2}}-1=base^2-1\)

由于base是奇数，设\(base=2n-1(n\ge1)\)，有

\[\begin{align}
g(3)=(2n-1)^2-1=4n^2-4n=4n(n+1)
\end{align}
\]

一定是8的倍数。故 \(2^3 \mid g(3)\)。

再结合递推公式，有

\[\begin{align}
\begin{cases}
2^{i} \mid g(i)\quad i\ge3\\
2^1 \mid g(i)\quad i=2\\
\end{cases}
\end{align}
\]

所以有

\[\begin{align}
2^{\frac{(3+i)(i-2)}{2}+1} \mid f(x)
\end{align}
\]

当 \(i=11\)时，刚好是\(2^{64}\)（真巧！）

如何避免被卡

• 随机base。相当于让不同位置上的权重不一样
• 双模数hash。
• 超大质数hash。既能像自然溢出一样有着大值域不易生日攻击，又不会被特殊的构造卡掉。