svtools prune具体算法

　　svtools具有不同的子命令以实现不同的功能，其中一个就是lmerge。根据其help信息(cluster and prune a BEDPE file by position based on allele frequency)可以看出，它是对BEDPE文件内的变异进行聚类和修剪的。

　　zcat ${input_vcf_gz} | svtools afreq | svtools vcftobedpe | svtools bedpesort | svtools prune -s -d 100 -e 'AF' | svtools bedpetovcf

　　这里是svt-pipeline所用的命令，一共分为afreq、vcftobedpe、bedpesort、prune、bedpetovcf几个步骤。这对这几个步骤分别进行解释。

　　(1)    afreq

　　这一步主要是对vcf文件添加一个等位频率的信息，即AF。我们这里所输入vcf文件是没有等位频率信息的，prune的修剪又是基于等位频率的，所以这里首先加上等位频率的信息。

图1.afreq执行之后的vcf INFO信息

　　上图所示，是afreq执行之后的vcf文件INFO信息，其中标红的位置是新加信息。添加了AF、NSAMP和MSQ信息。它们的含义可以在vcf文件的header部分找到，它们所代表的含义为：

　　AF, Description="Allele Frequency, for each ALT allele, in the same order as listed“

　　NSAMP, Description="Number of samples with non-reference genotypes"

　　MSQ, Description="Mean sample quality of positively genotyped samples"

　　这就是afreq所要做的。

　　(2)    vcftobedpe

　　vcftobedpe即把vcf文件转换为bedpe文件，这两个文件在变异描述的格式上有所不同，而prune是针对bedpe文件进行变异聚类和修剪的，所以要把文件格式进行转换。

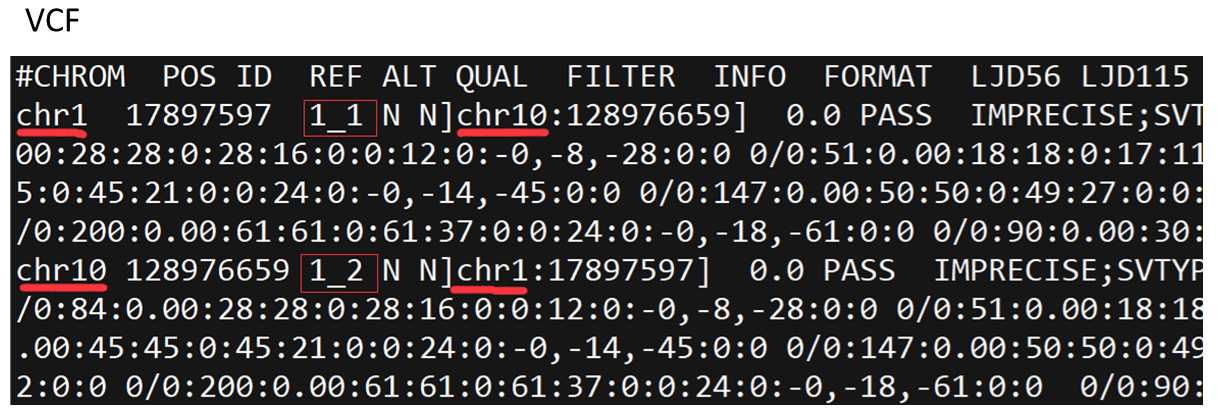
图2. 输入vcf文件

图3. 转换后的BEDPE文件

从图中可以看出，这里输入的vcf文件使用两行表示了同一个变异，使用1_1和1_2进行区分，但是在BEDPE文件中把这两行合并到了一行。

　　(3)    bedpesort

　　bedpesort是对bedpe文件的排序。下图是对bedpe文件进行排序的方法，可以看出是按前6列逐次进行的排序，即左侧染色体、左侧起始位置、左侧终止位置、右侧染色体、右侧起始位置、右侧终止位置。

图4. Bedpe排序方法

　　(4)    prune

　　接下来就是对已排序的bedpe文件进行聚类和修剪。在prune命令中会有三个常用的参数：-s，指定输入文件是经过排序的；-d指定一个碱基长度范围，用于后续聚类；-e指定一个指标，用于评估一个聚类内最优变异记录。

　　在把vcf文件转换为bedpe文件后，每个变异记录会有左侧起始位置、左侧终止位置和右侧起始位置、右侧终止位置，所有就构成了两个区间。Prune命令会按照-d参数指定的长度对这两个区间左右进行扩展，然后把这两个区间同时有重叠的变异记录放在一起成为一个聚类。然后遍历每个聚类内的记录，选择AF最大的那个记录作为最优记录，然后把其他记录里的SNAME信息添加到最优记录里，再把其他记录删除掉，作为修剪。

　　(5)    bedpetovcf

　　最后就是把bedpe文件重新转换为vcf文件。