ZJOI 2009 多米诺骨牌（状态压缩+轮廓线+容斥）

题意

https://www.lydsy.com/JudgeOnline/problem.php?id=1435

思路

一道很好的状压/容斥题，涵盖了很多比较重要的知识点。

我们称每两行间均有纵跨、每两列之间均有横跨为附加要求，我们先考虑没有附加要求的情况。直接存一行状态进行 \(dp\) 的话，似乎要枚举子集，复杂度挺大的。

这种类型的状压有一种比较神仙的优化方法——轮廓线。

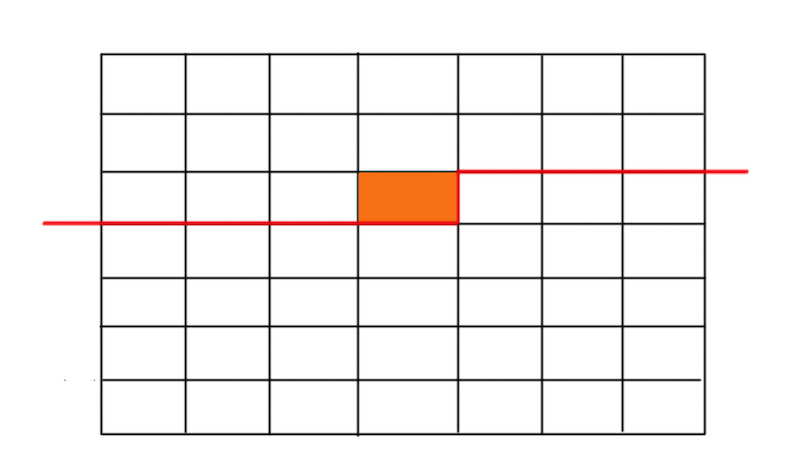
如上图所示，假如决策到的点是橙色的点，那么红线指的就是轮廓线，这种状压的方法可以会让状态数乘一个 \(n\) ，但是这样转移就是 \(O(1)\) 的，不需要枚举子集。

定义 \(dp_{i,j,k}\) 为决策到坐标 \((i,j)\) ，轮廓线状态为 \(k\) 的状态，就可以进行 \(O(1)\) 转移了，我们枚举左界、右界、上界，再用轮廓线 \(dp\) 往下扫，下面证明一下复杂度的正确性，不想看的可以跳过。

\[\begin{array}{}
T&=\displaystyle\sum_{i=1}^n\sum_{j=1}^i\sum_{k=1}^nk(i-j)2^{i-j}\\
&=\displaystyle\sum_{i=1}^n\sum_{j=1}^i(i-j)2^{i-j}\sum_{k=1}^nk\\
&=\displaystyle n^2\sum_{i=1}^n\sum_{j=1}^i(i-j)2^{i-j}
\end{array}
\]

注意证明复杂度时并不需要保证严格相等。我们令 \(d=i-j\) ，由于 \(j\in[1,i]\) ，故 \(d\in[0,i-1]\) 。

\[\begin{array}{}
T&=\displaystyle n^2\sum_{i=1}^n\sum_{d=0}^{i-1}d2^d
\end{array}
\]

\(\displaystyle\sum_{i=0}^{n}i2^i\) 这个玩意儿就是一个差比数列，数学必修五的常考点，这里就不详细写了，结果是一个 \(n2^{n+1}\) 级别的式子，我们继续化简。

\[\begin{array}{}
T&=\displaystyle n^2\sum_{i=1}^ni2^i\\
&=n^2\cdot n2^{n+1}\\
&=n^32^{n+1}
\end{array}
\]

连续套用两次，我们得到了一个比一开始的式子看起来优秀很多的复杂度，事实上常数也是比较小的。真正考试的时候其实也不需要这样证明，直接记一个 \(cnt\) 跑一遍极限数据就行了。

得到 \(dp\) 数组之后，加和一下便能得到 \(DP_{u,d,l,r}\) ，表示在以 \((u,l)\) 为左上角，\((d,r)\) 为右上角的矩形内，不用满足附加条件地放骨牌，总共的方案数。

然后我们考虑如何解决附加条件，这个条件看着就很容斥。

考虑先解决横跨列的条件，我们二进制枚举纵向分割线，表示这些分割线不得跨越的方案数，偶加奇减一下即可。

然后我们考虑纵跨行，再进行二进制枚举肯定复杂度太大了，但我们进行容斥通常有两种方法，一种是一个一个二进制枚举，另外一种写法叫做“代表元容斥”，它计算前 \(x\) 合法的状态数，再枚举合法到非法的第一个分界点，直接相减来计算答案。对于本题，可以枚举前 \(x\) 行的合法状态，然后再枚举横向分割线表示一定不纵跨，写成 \(dp\) 式就是：

\[f_i=g_{1,i}-\sum_{j=1}^{i-1}f_jg_{j+1,i}
\]

其中 \(g_{i,j}\) 表示第 \(i\) 行到第 \(j\) 行，不一定满足附加条件的方案数，\(f_i\) 表示前 \(i\) 行，满足附加条件的方案数。

注意二进制枚举容斥和代表元容斥各自的优越性，前者能解决的情况多，后者复杂度低。

代码

#include<bits/stdc++.h>
#define FOR(i,x,y) for(int i=(x),i##END=(y);i<=i##END;++i)
#define DOR(i,x,y) for(int i=(x),i##END=(y);i>=i##END;--i)
template<typename T,typename _T>inline bool chk_min(T &x,const _T y){return y<x?x=y,1:0;}
template<typename T,typename _T>inline bool chk_max(T &x,const _T y){return x<y?x=y,1:0;}
typedef long long ll;
const int P=19901013;
char str[18][18];
int DP[18][18][18][18];		//DP[u][d][l][r] 表示矩形(u,d,l,r)内骨牌摆放的方案数（不必满足附加要求）
int dp[18][18][(1<<15)+3];	//dp[x][y][B] 表示扫到坐标(x,y)，轮廓线的摆放状态为B的方案数（不必满足附加要求）
int f[18],g[18][18];		//f[x] 表示到第1行到第x行的方案数，满足附加要求
int bcnt[(1<<15)+3];		//g[x][y] 表示第x行到第y行到方案数，不必满足附加要求
int n,m;
inline void add(int &x,const int y)
{
	x+=y;
	if(x>=P)x-=P;
}
inline void sub(int &x,const int y)
{
	x-=y;
	if(x<0)x+=P;
}

void get_DP(int l,int r,int u)
{
	FOR(i,0,n-u)FOR(j,0,r-l)FOR(k,0,(1<<(r-l+1))-1)dp[i][j][k]=0;
	FOR(i,-1,n-u)FOR(j,0,r-l)
	{
		if((i==-1&&j!=r-l)||(i==n-u&&j==r-l))continue;
		int nxti=(j==r-l?i+1:i),nxtj=(j==r-l?0:j+1);
		FOR(k,0,(1<<(r-l+1))-1)
		{
			int ad=(i==-1?(k==(1<<(r-l+1))-1):dp[i][j][k]);
			if(!ad)continue;
			if(str[nxti+u][nxtj+l]=='x')add(dp[nxti][nxtj][k|(1<<nxtj)],ad);
			else
			{
				if(nxtj>0&&(k&(1<<(nxtj-1)))==0)
					add(dp[nxti][nxtj][k|(1<<(nxtj-1))|(1<<nxtj)],ad);
				if(nxti>0&&(k&(1<<nxtj))==0)
					add(dp[nxti][nxtj][k|(1<<nxtj)],ad);
				add(dp[nxti][nxtj][(k|(1<<nxtj))^(1<<nxtj)],ad);
			}
		}
	}
	FOR(i,0,n-u)FOR(j,0,(1<<(r-l+1))-1)
		add(DP[u][i+u][l][r],dp[i][r-l][j]);
}

int solve(int B)
{
	FOR(i,1,n)FOR(j,i,n)
	{
		g[i][j]=1;
		int las=1;
		FOR(k,1,m-1)if(B>>(k-1)&1)
		{
			g[i][j]=1ll*g[i][j]*DP[i][j][las][k]%P;
			las=k+1;
		}
		g[i][j]=1ll*g[i][j]*DP[i][j][las][m]%P;
	}
	FOR(i,1,n)
	{
		f[i]=g[1][i];
		FOR(j,1,i-1)
			sub(f[i],1ll*f[j]*g[j+1][i]%P);
	}
	return f[n];
}

int main()
{
	FOR(i,1,1<<15)bcnt[i]=bcnt[i>>1]+(i&1);
	scanf("%d%d",&n,&m);
	FOR(i,1,n)scanf("%s",str[i]+1);
	FOR(l,1,m)FOR(r,l,m)FOR(u,1,n)get_DP(l,r,u);
	int ans=0;
	FOR(i,0,(1<<(m-1))-1)
	{
		if(bcnt[i]&1)sub(ans,solve(i));
		else add(ans,solve(i));
	}
	printf("%d\n",ans);
	return 0;
}