反向传播（Back Propagation）

反向传播（Back Propagation）

通常在设计好一个神经网络后，参数的数量可能会达到百万级别。而我们利用梯度下降去跟新参数的过程如（1）。但是在计算百万级别的参数时，需要一种有效计算梯度的方法，这种方法就是反向传播（简称BP）， 因此BP并不是一种新的算法，使用BP就是能够使计算梯度时更加有效率。

其中θ为神经网络的参数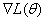，为梯度。

链式法则

设有两个函数为y=g(x),z=h(y)，那么要计算z对x导数，则计算过程如（2）

设有三个函数为x=g(s),y=h(s),z=k(x,y)，那么要计算z对x导数，则计算过程如（3）

BP计算过程

假定我们设计的神经网络结构如图1-1所示，其中y_j神经网络为输出值，d_h为隐藏层神经元的输出值，x_i为输入值，b_j、m_h分别是隐藏层和输出层神经元的偏置；

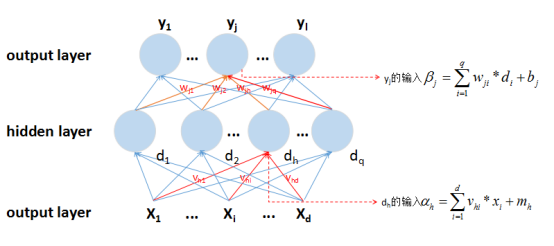
图1-1 神经网络结构

设神经网络的损失函数为L(θ)（L(θ)具体的结构根据实际情况来确定，θ表示所有参数）；w_jh的更新形式为

由于w_jh是通过影响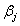，继而影响y_j，最终影响L(θ)。因此w_jh的更新计算可以通过（2）的链式法则进行展开。

其中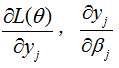，需要在确定激活函数和损失函数的具体结果后才就可以进行微分。而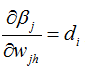则可以在神经网络前向传播的过程中就可以计算，因此这一项的计算是自下向上，因此也称作forward pass。

类比于w_jh的更新情况，b_j的更新计算为

再计算v_hi的的更新情况，跟w_jh的更新情况没有太大差别。v_hi通过影响输入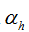，继而影响d_h，d_h通过影响所有的输出层神经元的输入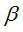，继而影响输出值Y={y₁,y₂,...y_l}，最终影响L(θ)，因此需要运用（3）进行链式法则展开

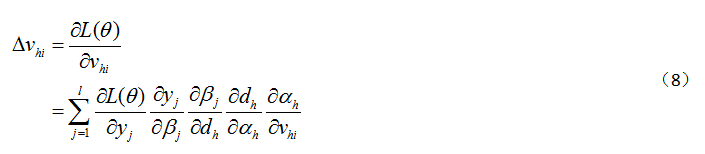
其中（8）中的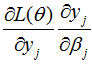跟计算的部分项相同。因此，要计算下层参数的微积分，就需要计算上层参数的微积分。整个参数的更新计算自上向下，这个计算过程也称作backward pass。

参考资料

[1]机器学习-李宏毅

[2]《机器学习》-周志华