P1073 最优贸易（最短路）

题目描述

CC C国有n n n个大城市和m mm 条道路，每条道路连接这 nnn个城市中的某两个城市。任意两个城市之间最多只有一条道路直接相连。这 mmm 条道路中有一部分为单向通行的道路，一部分为双向通行的道路，双向通行的道路在统计条数时也计为 11 1条。

CC C国幅员辽阔，各地的资源分布情况各不相同，这就导致了同一种商品在不同城市的价格不一定相同。但是，同一种商品在同一个城市的买入价和卖出价始终是相同的。

商人阿龙来到 CCC 国旅游。当他得知同一种商品在不同城市的价格可能会不同这一信息之后，便决定在旅游的同时，利用商品在不同城市中的差价赚回一点旅费。设 CCC 国 n 个城市的标号从 1 n1~ n1 n，阿龙决定从 11 1号城市出发，并最终在 nnn 号城市结束自己的旅行。在旅游的过程中，任何城市可以重复经过多次，但不要求经过所有 nnn 个城市。阿龙通过这样的贸易方式赚取旅费：他会选择一个经过的城市买入他最喜欢的商品――水晶球，并在之后经过的另一个城市卖出这个水晶球，用赚取的差价当做旅费。由于阿龙主要是来 CCC 国旅游，他决定这个贸易只进行最多一次，当然，在赚不到差价的情况下他就无需进行贸易。

假设 CC C国有 555个大城市，城市的编号和道路连接情况如下图，单向箭头表示这条道路为单向通行，双向箭头表示这条道路为双向通行。

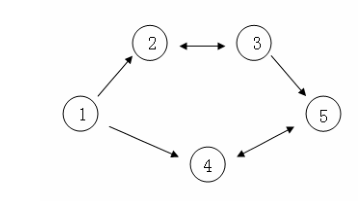
假设 1 n1~n1 n 号城市的水晶球价格分别为 4,3,5,6,14,3,5,6,14,3,5,6,1。

阿龙可以选择如下一条线路：111->222->333->555，并在 22 2号城市以3 33 的价格买入水晶球，在 333号城市以5 5 5的价格卖出水晶球，赚取的旅费数为 2。

阿龙也可以选择如下一条线路1 11->444->555->444->555，并在第11 1次到达5 55 号城市时以 11 1的价格买入水晶球，在第 222 次到达4 44 号城市时以6 66 的价格卖出水晶球，赚取的旅费数为5 55。

现在给出 nn n个城市的水晶球价格，mmm 条道路的信息（每条道路所连接的两个城市的编号以及该条道路的通行情况）。请你告诉阿龙，他最多能赚取多少旅费。

输入输出格式

输入格式：

第一行包含 222 个正整数n n n和 mmm，中间用一个空格隔开，分别表示城市的数目和道路的数目。

第二行 n 个正整数，每两个整数之间用一个空格隔开，按标号顺序分别表示这 n 个城市的商品价格。

接下来 mmm 行，每行有3 3 3个正整数x,y,zx,y,zx,y,z，每两个整数之间用一个空格隔开。如果 z=1z=1z=1，表示这条道路是城市x x x到城市y y y之间的单向道路；如果z=2 z=2z=2，表示这条道路为城市 xx x和城市yy y之间的双向道路。

输出格式：

一 个整数，表示最多能赚取的旅费。如果没有进行贸易，则输出 000。

输入输出样例

输入样例#1： 复制

5 5
4 3 5 6 1
1 2 1
1 4 1
2 3 2
3 5 1
4 5 2 

输出样例#1： 复制

5

说明

【数据范围】

输入数据保证 111 号城市可以到达n n n号城市。

对于 10%的数据，1≤n≤61≤n≤61≤n≤6。

对于 30%的数据，1≤n≤1001≤n≤1001≤n≤100。

对于 50%的数据，不存在一条旅游路线，可以从一个城市出发，再回到这个城市。

对于 100%的数据，1≤n≤1000001≤n≤1000001≤n≤100000，1≤m≤5000001≤m≤5000001≤m≤500000，1≤x1≤x1≤x，y≤ny≤ny≤n，1≤z≤21≤z≤21≤z≤2，1≤1≤1≤各城市

水晶球价格≤100≤100≤100。

NOIP 2009 提高组 第三题

题解：

题目大意就是求出来最大价格差，所以要先求一下在最短路期间的的每一条路上路过的城市的最小值，求完之后还要再求一下每条路上的路过城市的最大值

要注意这个两次最短路期间求极值的时候我们要一个选择城市的路径按题目上给出的，另一个要把存路径的数组中的道路反过来

为什么要这样？

正着求一次表示每一次从起点开始的路径到达这一条路上的某个城市的时候，加上之前经过的这条路上的所有城市中目前价格最低的

反着题目给出的路径这一种求最大值的最短路，意思是从终点开始的每一条路上，这个城市加上之前经过的这条路上的所有城市中目前价格最高的

这个样子如果正着路径经过一个城市，反正路径也经过了那个城市，那就说明可以从起点中途经过这个点到达终点

最后可以对所有的这些点进行枚举来找出价格差最大

具体实现看代码：

  1 #include<cstdio>
  2 #include<cstring>
  3 #include<iostream>
  4 #include<algorithm>
  5 #include<vector>
  6 #include<queue>
  7 using namespace std;
  8 typedef long long ll;
  9 const int maxn=100005;
 10 const int INF=0x3f3f3f3f;
 11 struct shudui
 12 {
 13     int start;
 14 }str1,str2;
 15 queue<int>r;
 16 int v[maxn],d1[maxn],vis[maxn],n,d2[maxn];
 17 vector<shudui>w[maxn];
 18 vector<shudui>ww[maxn];
 19 void spay(int d[maxn])
 20 {
 21     memset(vis,0,sizeof(vis));
 22
 23     r.push(1);
 24     d[1]=v[1];
 25     vis[1]=1;
 26     while(!r.empty())
 27     {
 28         int x=r.front();
 29         r.pop();
 30         vis[x]=0;
 31         for(int i=0;i<w[x].size();++i)
 32         {
 33             int y=w[x][i].start;
 34             if(d[y]>min(d[x],v[y]))
 35             {
 36                 d[y]=min(d[x],v[y]);
 37                 if(!vis[y])
 38                 {
 39                     r.push(y);
 40                     vis[y]=1;
 41                 }
 42             }
 43         }
 44     }
 45 }
 46 void spay2(int d[maxn])
 47 {
 48     memset(vis,0,sizeof(vis));
 49     r.push(n);
 50     d[n]=v[n];
 51     vis[n]=1;
 52     while(!r.empty())
 53     {
 54         int x=r.front();
 55         r.pop();
 56         vis[x]=0;
 57         for(int i=0;i<ww[x].size();++i)
 58         {
 59             int y=ww[x][i].start;
 60             if(d[y]<max(d[x],v[y]))
 61             {
 62                 d[y]=max(d[x],v[y]);
 63                 if(!vis[y])
 64                 {
 65                     r.push(y);
 66                     vis[y]=1;
 67                 }
 68             }
 69         }
 70     }
 71 }
 72 int main()
 73 {
 74     int m;
 75     scanf("%d%d",&n,&m);
 76     for(int i=1;i<=n;++i)
 77         scanf("%d",&v[i]);
 78     while(m--)
 79     {
 80         int x,y,z;
 81         scanf("%d%d%d",&x,&y,&z);
 82         if(z==1)
 83         {
 84             str2.start=y;
 85             w[x].push_back(str2);
 86             str2.start=x;
 87             ww[y].push_back(str2);
 88         }
 89         else
 90         {
 91             str2.start=y;
 92             w[x].push_back(str2);
 93             str2.start=x;
 94             w[y].push_back(str2);
 95             str2.start=y;
 96             ww[x].push_back(str2);
 97             str2.start=x;
 98             ww[y].push_back(str2);
 99         }
100     }
101     memset(d1,INF,sizeof(d1));
102     //printf("%d\n",d1[1]);
103     spay(d1);
104     memset(d2,0,sizeof(d2));
105     spay2(d2);
106     int maxx=0;
107     for(int i=1;i<=n;++i)
108     {
109         //if(d2[i]!=INF && d1[i]!=0)
110         maxx=max(maxx,d2[i]-d1[i]);
111     }
112     printf("%d\n",maxx);
113     return 0;
114 }