4.9 省选模拟赛 划分序列 二分 结论 树状数组优化dp

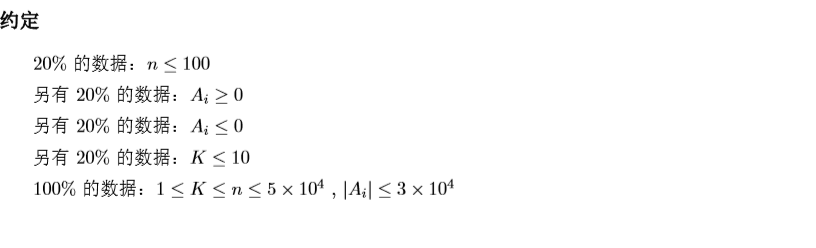
显然发现可以二分。

对于n<=100暴力dp f[i][j]表示前i个数分成j段对于当前的答案是否可行。

可以发现这个dp是可以被优化的 sum[i]-sum[j]<=mid sum[i]-mid<=sum[j]

维护一个最大的sumj 即可O(1)转移 复杂度nklog 可以获得 40分。

考虑ai>=0 二分完之后直接贪心即可 能选就选 可以证明 这是最优的或者说对后面结果不会更差。

考虑ai<=0 二分完之后可以发现能分成一段就分成一段 只要分的段数>=k即可。

这样总共就可以获得80分了。

code:

const int MAXN=50010,maxn=110;
int n,k,maxx,minn,ans;
int a[MAXN],sum[MAXN];
int f[MAXN][maxn];//f[i][j]表示前i段分成j段是否可行.
int g[MAXN];//g表示在选出若干段满足条件时的段数是多少.
inline int check3(int x)
{
	f[0][0]=1;
	rep(1,k,j)
	{
		int mn=j==1?0:-INF;
		rep(1,n,i)
		{
			if(mn>=sum[i]-x)f[i][j]=1;
			else f[i][j]=0;
			if(f[i][j-1])mn=max(mn,sum[i]);
		}
	}
	return f[n][k];
}
inline int check2(int x)
{
	int cnt=0,sum=a[1];
	rep(2,n,i)
	{
		if(sum<=x)
		{
			++cnt;
			sum=a[i];
		}
		else sum+=a[i];
	}
	if(sum<=x)++cnt;
	return cnt>=k;
}
inline int check1(int x)
{
	int cnt=0,sum=a[1];
	rep(2,n,i)
	{
		if(a[i]>x)return 0;
		if(sum+a[i]<=x)sum+=a[i];
		else ++cnt,sum=a[i];
	}
	return cnt<=k-1;
}
inline int check4(int x)//选出若干段使得权值<=x
{
	int mn=0,p=0;
	rep(1,n,i)
	{
		if(mn>=sum[i]-x)g[i]=g[p]+1;
		else g[i]=-1;
		if(sum[i]>mn&&g[i]!=-1)
		{
			mn=sum[i];p=i;
		}
	}
	return g[n]!=-1;
}
inline int check(int x)//每选出一段 权值加x
{
	int l=minn,r=maxx;
	while(l<r)//在有附加值的时候继续二分最小值.
	{
		int mid=(l+r)>>1;
		if(check4(mid-x))r=mid;
		else l=mid+1;
	}
	check4(r-x);ans=r-x;
	if(g[n]==-1)return 0;
	return g[n]<=k;
}
int main()
{
	freopen("divide.in","r",stdin);
	freopen("divide.out","w",stdout);
	get(n);get(k);
	int flag1=0,flag2=0;
	rep(1,n,i)
	{
		get(a[i]);
		sum[i]=sum[i-1]+a[i];
		if(a[i]<0)flag1=1,minn+=a[i];
		if(a[i]>0)flag2=1,maxx+=a[i];
	}
	if(!flag1)//ai>=0
	{
		int l=minn,r=maxx;
		while(l<r)
		{
			int mid=(l+r)>>1;
			if(check1(mid))r=mid;
			else l=mid+1;
		}
		put(r);return 0;
	}
	if(!flag2)//ai<=0
	{
		int l=minn,r=maxx;
		while(l<r)
		{
			int mid=(l+r)>>1;
			if(check2(mid))r=mid;
			else l=mid+1;
		}
		put(r);return 0;
	}
	if(n<=100||k<=100)
	{
		int l=minn,r=maxx;
		while(l<r)
		{
			int mid=(l+r)>>1;
			if(check3(mid))r=mid;
			else l=mid+1;
		}
		put(r);return 0;
	}
	return 0;
}

从中我们发现第一个dp很接近正解了 K一定是可以被优化掉的。恰好K段->WQS二分，广义容斥啥的。

这道题 很有趣 从第二个部分分 可以发现 我们得到最小分的段数x 对于K>=x都是可以的。

第三个部分分 得到最大的分段数 对于K<=x都是可以的。

从中我们可以猜想 对于 一个答案mid 求出最多的分段 求出最小的分段 那么处于中间的K段就是可行的。

我也不会证明hh...但是题目提示的很明显 这也算是一道结论题吧 暴力打表或许可以证明。

这样K就被我们优化掉了 把先前的dp改一下 表示最多/最少分的段数 发现这个很容易使用树状数组优化(常数也小。

总复杂度nlog^2.

const int MAXN=50010<<1,maxn=110;
int n,k,maxx,minn,ans,num,cnt;
int a[MAXN],sum[MAXN];
int f[MAXN],b[MAXN];
int c[MAXN];
int s1[MAXN],s2[MAXN];
inline int ask(RE int x)
{
	int cnt=INF;
	while(x)
	{
		cnt=min(cnt,c[x]);
		x-=x&(-x);
	}
	return cnt;
}
inline void insert(RE int x,RE int y)
{
	while(x<=num)
	{
		if(c[x]<=y)return;
		c[x]=min(c[x],y);
		x+=x&(-x);
	}
}
inline int ask1(RE int x)
{
	int cnt=-INF;
	while(x)
	{
		cnt=max(cnt,c[x]);
		x-=x&(-x);
	}
	return cnt;
}
inline void insert1(RE int x,RE int y)
{
	while(x<=num)
	{
		if(c[x]>=y)return;
		c[x]=max(c[x],y);
		x+=x&(-x);
	}
}
inline int check(RE int x)
{
	cnt=n;
	rep(1,n,i)b[i]=sum[i],b[++cnt]=sum[i]-x;
	b[++cnt]=0;num=0;
	sort(b+1,b+1+cnt);
	rep(1,cnt,i)if(i==1||b[i]!=b[i-1])b[++num]=b[i];
	s1[0]=num+1-(lower_bound(b+1,b+1+num,0)-b);
	rep(1,num,i)c[i]=INF;
	insert(s1[0],0);
	rep(1,n,i)
	{
		s1[i]=num+1-(lower_bound(b+1,b+1+num,sum[i])-b);
		s2[i]=num+1-(lower_bound(b+1,b+1+num,sum[i]-x)-b);
		f[i]=ask(s2[i])+1;
		if(f[i]<n)insert(s1[i],f[i]);
	}
	if(f[n]>k)return 0;
	rep(1,num,i)c[i]=-INF;
	insert1(s1[0],0);
	rep(1,n,i)
	{
		f[i]=ask1(s2[i])+1;
		if(f[i]<n)insert1(s1[i],f[i]);
	}
	if(f[n]<k)return 0;
	return 1;
}
int main()
{
	freopen("divide.in","r",stdin);
	freopen("divide.out","w",stdout);
	get(n);get(k);
	rep(1,n,i)
	{
		get(a[i]);
		sum[i]=sum[i-1]+a[i];
		if(a[i]<=0)minn+=a[i];
		if(a[i]>=0)maxx+=a[i];
	}
	int l=minn,r=maxx;
	while(l<r)
	{
		int mid=(l+r)>>1;
		if(check(mid))r=mid;
		else l=mid+1;
	}
	put(l);return 0;
}