数据结构实验代码分享 - 3 （哈夫曼树 / HuffmanTree）

哈夫曼编码/ 译码系统（树应用）

[问题描述]

任意给定一个仅由 26 个大写英文字母组成的字符序列，根据哈夫曼编码算法，求得每个字符的哈夫曼编码。

要求：

1）输入一个由 26 个英文字母组成的字符串，请给出经过哈夫曼编码后的编码序列及其编码程度。（编码）

2）采用上一问题的哈夫曼编码，给定一串编码后的序列，将其翻译为原字符序列。（解码）

样例：

输入原串：CASBCATBSATBAT

输出：

A 00

B 10

T 11

C 010

S 011

输入：0100011

输出：CAT

设计思路

自顶向下拆解：

　　1. 编码部分（Encode）

　　　　a)　　输入字符串；

　　　　b)　　根据输入的字符串创建HuffmanTree；

　　　　c)　　遍历HuffmanTree 得到各结点的HuffmanCode；

　　　　d)　　收集各个叶节点的字符及其HuffmanCode，做成HuffmanCodeTable并输出。

　　　　 注：由HuffmanTree的构造方法可知：叶节点 <=> “有效字符”

　　2. 译码部分（Decode）

　　　　a)　　输入密文字符串；

　　　　b)　　在HuffmanCodeTable中逐字匹配以找到明文字符 / 或是直接遍历HuffmanTree即可；

　　　　c)　　输出明文字符串。

思维导图如下：

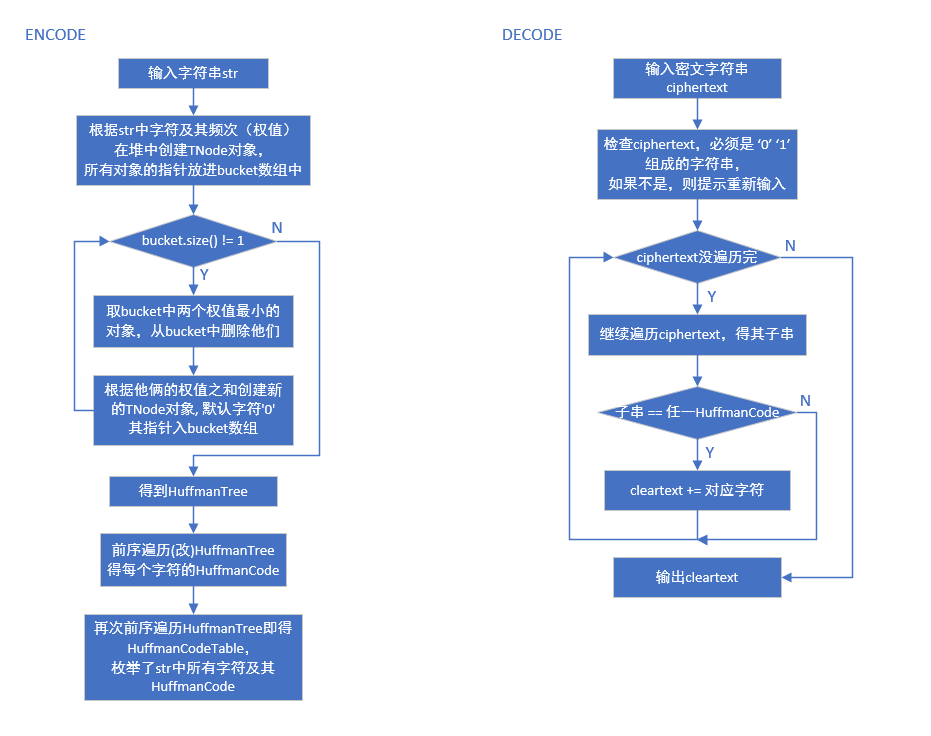
代码实现

两个类：

 1 class HuffmanTNode  // 用于Encode时的HuffmanTree
 2 {
 3 public:
 4     char ch;     // 字符
 5     int weight;  // 权值、频次
 6     HuffmanTNode* lchild;
 7     HuffmanTNode* rchild;
 8     string HuffmanCode;
 9
10     HuffmanTNode() : HuffmanCode(), lchild(nullptr), rchild(nullptr) {}
11     HuffmanTNode(char a, int wei) : ch(a), weight(wei), HuffmanCode(), lchild(nullptr), rchild(nullptr) {}
12     HuffmanTNode(const HuffmanTNode &other) : ch(other.ch), weight(other.weight), HuffmanCode(other.HuffmanCode),
13                                             lchild(other.lchild), rchild(other.rchild) {}
14     ~HuffmanTNode() {
15         // 对左右子树的递归清理
16         if (lchild != nullptr) {
17             delete lchild;
18         }
19         lchild = nullptr;
20         if (rchild != nullptr) {
21             delete rchild;
22         }
23         rchild = nullptr;
24     }
25 };
26
27 class HuffmanCharAndCode    // 用于Decode时的查找表
28 {
29 public:
30     char ch;    // 字符
31     string HuffmanCode; // 哈夫曼编码
32
33     HuffmanCharAndCode() {}
34     HuffmanCharAndCode(char a, const string &code) : ch(a){
35         HuffmanCode += code;
36     }
37     ~HuffmanCharAndCode() {}
38 };

包装类 * 2

Encode：

　　1. main() 函数展示了程序的主干，如下：

 1 int main() {
 2
 3     /*************************ENCODE*************************/
 4     // 1 输入字符串
 5     printf("ENCODE: \n");
 6     string str;
 7     printf("plz Enter String :");
 8     std::cin >> str;
 9
10     // 2 根据输入的字符串创建HuffmanTree
11     HuffmanTNode* root = CreateHuffmanTree(str);
12     while (root == nullptr) {   // 非法输入字符串的处理
13         printf("\nERROR! Invalid Input!\n");
14         printf("plz Enter String Again :");
15         std::cin >> str;
16         root = CreateHuffmanTree(str);
17     }
18
19     // 3 根据生成的HuffmanTree得到HuffmanCodeTable
20     vector<char> vec_code;
21     GetHuffmanCode(root, vec_code);
22     vector<HuffmanCharAndCode*> HuffmanCodeTable;
23     GetHuffmanCodeTable(root, HuffmanCodeTable);
24
25     // 4 输出字符及其对应的HuffmanCode
26     printf("\nSUCCESS! the HuffmanCode is listed as below: \n");
27     std::sort(HuffmanCodeTable.begin(), HuffmanCodeTable.end(), compare_CodeTable);
28     OutputHuffmanCode(HuffmanCodeTable);
29
30     /*************************DECODE*************************/
31
32     // 1 输入密文字符串
33     printf("\nDECODE: \n");
34     string ciphertext;
35     printf("plz Enter CipherText :");
36     std::cin >> ciphertext;
37
38     // 2 解码密文字符串得到明文
39     string cleartext;
40     int error_index = 1;
41     while (HuffmanDecode(ciphertext, HuffmanCodeTable, cleartext, error_index) == false) {  // 非法密文字符串的处理
42         printf("\nERROR! Invalid Input Ciphertext!\n");
43         printf("\nthe POTENTIAL index of error char in at: %d\n", error_index);
44         printf("plz Enter CipherText Again :");
45         std::cin >> ciphertext;
46     }
47
48     // 3 输出明文字符串
49     printf("SUCCESS! the ClearText is: \n");
50     std::cout << cleartext << std::endl;
51
52     // 释放HuffmanTable
53     for (HuffmanCharAndCode* elem : HuffmanCodeTable) {
54         delete elem;
55     }
56
57     system("pause");
58     return 0;
59 }

main()

　　2. 创建HuffmanTree()，如下：

 1 HuffmanTNode* CreateHuffmanTree(const string &str) {
 2     // 字符串检查
 3     if (str.size() == 0) { return nullptr; }
 4     // 字符频次记录桶
 5     vector<HuffmanTNode*> bucket;
 6     // 填充字符频次记录桶
 7     if (FillCharFrequencyBucket(str, bucket) == false) { return nullptr; }
 8     // 若只有一个字符 那么没必要用哈夫曼编码
 9     if (bucket.size() == 1) { return nullptr; }
10
11
12     // 当bucket中只剩下一个元素，那么它就是HuffmanTree的root
13     while (bucket.size() != 1) {
14         // 令bucket中元素按weight非递增排序
15         std::sort(bucket.begin(), bucket.end(), compare_bucket);
16
17         // 从bucket中取两个最小的elem
18         HuffmanTNode *elem_1 = bucket[bucket.size() - 1];   bucket.pop_back();
19         HuffmanTNode *elem_2 = bucket[bucket.size() - 1];   bucket.pop_back();
20         // 根据 elem1 与 elem2 的weight 得到它俩的 root
21         HuffmanTNode *root_tmp = new HuffmanTNode('\0', elem_1->weight + elem_2->weight);
22         // root_tmp, elem_1, elem_2 三者组成三结点的二叉树
23         root_tmp->lchild = elem_2;
24         root_tmp->rchild = elem_1;
25
26         // root_tmp 入桶
27         bucket.push_back(root_tmp);
28     }
29
30     // bucket中最后元素，就是哈夫曼树的根节点指针
31     HuffmanTNode *root = bucket[0];
32     return root;
33 }

CreateHuffmanTree()

　　3. 遍历得到各结点HuffmanCode，再收集各个叶节点的Code即可，我就只放前者吧，稍微有趣一点，如下：

 1 // 将vec_code中的字符转为字符串 并赋给当前节点curr->HuffmanCode
 2 void visit(HuffmanTNode *curr, const vector<char> &vec_code) {
 3     string Code(vec_code.begin(), vec_code.end());
 4     curr->HuffmanCode = Code;
 5 }
 6
 7 // （前序遍历改） 得到HuffmanTree上每个结点的HuffmanCode
 8 void GetHuffmanCode(HuffmanTNode *root, vector<char> vec_code) {
 9     if (root != nullptr) {
10         visit(root, vec_code);
11         vec_code.push_back('0');
12         GetHuffmanCode(root->lchild, vec_code);
13         vec_code.pop_back();
14         vec_code.push_back('1');
15         GetHuffmanCode(root->rchild, vec_code);
16         vec_code.pop_back();
17     }
18 }

先序遍历改，得各结点的HuffmanCode

Decode：

　　好像不是很难，就不放了，照着思路往下做就行。（主要我写的不是很好看...)

运行结果

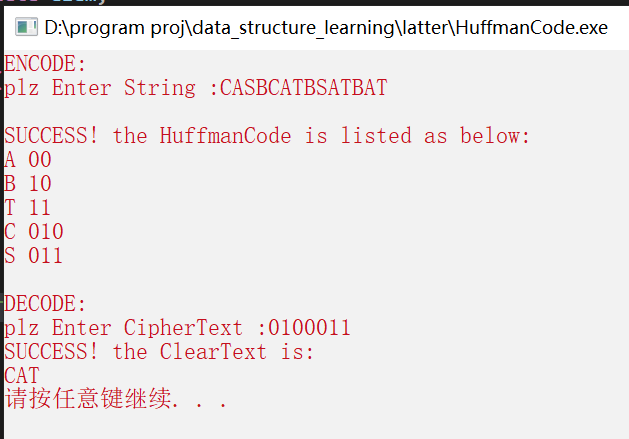
ps: HuffmanCode不是唯一的，是根据你生成的HuffmanTree 和 你定义的Code规则而定，比如说我的Code规则是左0右1。

行，那就先这样吧，这代码写了好久都有些遗忘了，幸好之前做了思维导图，希望能帮助到你。