k 分算法是 k 越大越好吗？

引入

我们有二分算法，就是：

定义

二分查找（英语：binary search），也称折半搜索（英语：half-interval search）、对数搜索（英语：logarithmic search），是用来在一个有序数组中查找某一元素的算法。

过程

以在一个升序数组中查找一个数为例。

它每次考察数组当前部分的中间元素，如果中间元素刚好是要找的，就结束搜索过程；如果中间元素小于所查找的值，那么左侧的只会更小，不会有所查找的元素，只需到右侧查找；如果中间元素大于所查找的值同理，只需到左侧查找。

能不能有三分算法呢？正当我以为这是一个天才的想法时，我发现：

如果需要求出单峰函数的极值点，通常使用二分法衍生出的三分法求单峰函数的极值点。

三分法与二分法的基本思想类似，但每次操作需在当前区间 \([l,r]\)内任取两点 \(lmid,rmid(lmid < rmid)\)。如果 \(f(lmid)<f(rmid)\)，则在 \([rmid,r]\)中函数必然单调递增，最小值所在点（下图中的绿点）必然不在这一区间内，可舍去这一区间。反之亦然。

以上皆来自OI-WIKI

---

注意，这里我指的三分并不是求单峰函数中的三分，它只能求单调函数，每次去掉三分之二的部分。

那么，既然有三分了，有没有四分、五分、六分甚至 \(k\) 分呢？\(k\) 分算法存在有意义吗（\(k>3\)）？\(k\) 分算法是 \(k\) 越大越好吗？

于是，我的思索开始了。

本文仅代表个人观点，计算过程如有不严谨，希望您原谅并指出，时间复杂度忽略了部分时间，不代表最终结果。

最后 sto各位大佬

思索

\(k\) 分算法的复杂度为 \(k\log_kN\)，那么我们就需要知道 \(k\) 取什么才能让它最小。

证明

下面我们证明

\[f(k)=k\log_kN
\]

在 \(k>1,N>1\) 情况下的极小值时 \(k\) 的取值。

当我们要证明一个函数的极小值时的取值时，我们可以通过求导的方式。那么我们不得不引出导数这个概念。

我懒得写，大家请看：这里

那么一句话总结，导数就是函数在某点的切线的斜率，例如下面这张图：

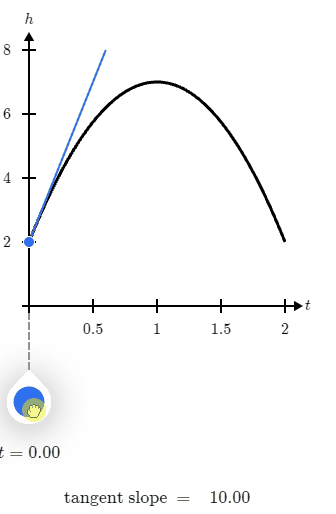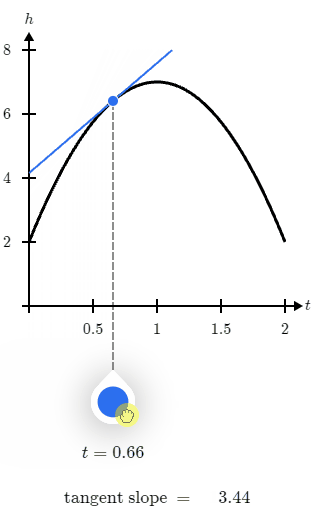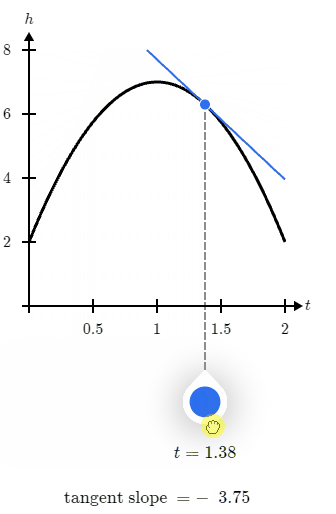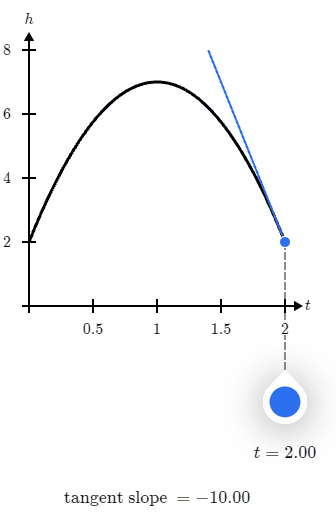
那么在导数函数结果等于0时，当前结果是极大值还是极小值呢？

极大值

噢，错啦

极小值

噢，错啦

其他（干脆你说你想看答案）

答对啦，正确答案是有可能是极大值也有可能是极小值（没想到吧）

往下翻

当导数函数结果等于0时，当前有可能是最大值也有可能是极小值，我们称这个点为临界点。我们可以检查临界点的邻域，即临界点的左右两侧。如果在临界点的左侧函数值递增，右侧函数值递减，则该点为最大值。如果在临界点的左侧函数值递减，右侧函数值递增，则该点为极小值。

接下来，我们的问题就变成了求：

\[f'(k)=0
\]

时 \(k\) 的取值。

$f'$ 是什么

就是 $f$ 函数的导数

根据换底公式， \(\log_kN = \frac{\ln N}{\ln k}\)，我们可以将 \(f(k)\) 重写为 \(f(k) = \frac{k}{\ln k} \ln N\)。

换底公式证明

要证明 $\log_kN=\frac{\log_bN}{\log_bk}$ （换底公式）
$$
\text{设} y=\log_kN
$$

\[k^y=N
\]

\[\log_bk^y=\log_bN
\]

\[y\log_bk=\log_bN
\]

\[y=\frac{\log_bN}{\log_bk}
\]

首先，可以使用乘法法则对函数 \(f(k)\) 进行求导。

根据乘法法则，若有两个函数 \(u(k)\) 和 \(v(k)\)，那么：

\[(u(k)\cdot v(k))'=u'(k)\cdot v(k)+u(k)\cdot v'(k)
\]

代入它，得到：

\[f'(k) = (\frac{k}{\ln k})'\cdot(\ln N)+(\frac{k}{\ln k})\cdot(\ln N)'
\]

其中，我们知道， \(N\) 是一个常数，那么 \(\ln N\) 也是一个常数。根据导数的定义，常数的导数为0。

你要我证明？

你看，常数的斜率不就是0吗

我们现在化简后知道：

\[f'(k) = (\frac{k}{\ln k})'\cdot(\ln N)
\]

那么，\((\frac{k}{\ln k})'\) 又是多少呢？

这时，我们的任务变成了求 \((\frac{k}{\ln k})'\)，可以使用除法法则进行求导。

根据除法法则，若有两个函数 \(u(k)\) 和 \(v(k)\)，那么：

\[(\frac{u(k)}{v(k)})' = \frac{u'(k)\cdot v(k)-u(k)\cdot v'(k)}{v(k)^2}
\]

代入它，得到：

\[(\frac{k}{\ln k})' = \frac{k'\cdot (\ln k)-k\cdot (\ln k)'}{\ln^2 k}
\]

因为 \(k\) 是一个自变量，所以它的导数为1（可以画图看，它的斜率是不是1），同时根据导数表，我们知道 \(\ln(k)'=\frac{1}{k}\)，代入得：

\[(\frac{k}{\ln k})' = \frac{\ln k-k\cdot\frac{1}{k}}{\ln^2 k} = \frac{\ln (k)-1}{\ln^2 k}
\]

再代回上面那个：

\[f'(k) = (\frac{k}{\ln k})'\cdot(\ln N) = \frac{(\ln N)(\ln (k)-1)}{\ln^2 k}
\]

求导完成，撒花！！！\(@⁰@)/

然后就简单了，因为

\[f'(k) = 0
\]

所以：

\[\frac{(\ln N)(\ln (k)-1)}{\ln^2 k} = 0
\]

所以：

\[(\ln N)(\ln (k)-1) = 0
\]

因为 \(N > 1\)，所以 \(\ln (k)-1=0\)，\(\ln k=1\)

那么 \(k\) 是几？当然是 \(k=e\) 啦！！！

大家感兴趣的还可以尝试二阶导数，然后判断二阶导数是否大于0，当二阶导数大于零时，该点为极小值点；当该点的二阶导数小于零时，该点为极大值点。（费马引理）

下面补上二阶导数的计算过程：

因为 \((c\cdot u(k))'=c\cdot u'(k)\) （大家可以用乘法法则自己证一下，这里 \(c\) 为常数）

\[f''(k) = \frac{(\ln N)(\ln (k)-1)}{\ln^2 k}
\]

\[\Downarrow
\]

\[f''(k) = \ln N\cdot(\frac{\ln (k)-1}{\ln^2k})'
\]

根据除法法则：

\[\ln N\cdot (\frac{(\ln(k)-1)'\cdot\ln^2k-(\ln(k)-1)\cdot(\ln^2k)'}{\ln^4k})
\]

根据加减法则（\((u(k)-v(k))'=u'(k)-v'(k)\)）：

\[\ln N\cdot\frac{((\ln k)'-(1)')\cdot\ln^2k-(\ln(k)-1)\cdot(\ln^2k)'}{\ln^4k}
\]

\[\Downarrow
\]

\[\ln N\cdot\frac{(\frac{1}{k}-0)\cdot\ln^2k-(\ln(k)-1)\cdot(\ln^2k)'}{\ln^4k}
\]

根据链式法则（设 \(y=f(u),u=g(k)\)，则 \(y'(k)=f'(u)\cdot g'(k)\)），且因为 \((x^\alpha)'=\alpha x^{\alpha-1}\)

\[\ln N\cdot\frac{\frac{1}{k}\cdot\ln^2k-(\ln(k)-1)\cdot((\ln k)^2)'}{\ln^4k}
\]

\[\ln N\cdot\frac{\frac{1}{k}\cdot\ln^2k-(\ln(k)-1)\cdot((2 \ln k)\cdot(\ln k)')}{\ln^4k}
\]

\[\Downarrow
\]

\[\ln N\cdot\frac{\frac{1}{k}\cdot\ln^2k-2(\ln(k)-1)\cdot\ln k\cdot\frac{1}{k}}{\ln^4k}
\]

\[\ln N\cdot\frac{\frac{\ln^2k}{k}-\frac{2(\ln(k)-1)\cdot\ln k}{k}}{\ln^4k}
\]

我们发现，当 \(k=e\) 该二阶导数大于0，故该点为极小值点。

那么好了，当我们进行 \(e\) 分时时间复杂度最少，但是我们总不能进行 2.718 分吧？所以我们取一个整数值，2或者3。

代入后可以得到，3的斜率更小，故选择3。

---

upd：假的，二分更优，因为三分查询数组次数过多当数据大（10000组10000000的数据）时会慢几毫秒