AcWing 456. 车站分级

原题链接AcWing 456. 车站分级

抽象出题意，停靠过的车站的等级一定严格大于为停靠过的车站的等级，且不存在环，例如车站\(A\)等级大于车站\(B\)，则\(A >= B + 1\)，不妨从\(B\)向\(A\)连一条边，表示等级关系，题目要求车站的最小等级中最大是多少，即求最长路，那这就是一个差分约束系统。

而对于差分约束系统：

如果边权有正有负：则使用\(spfa\)

如果边权非负，那么可以使用\(tarjan\)缩点+递推，\(拓扑排序 + 递推\)的方式求最长路或者最短路。

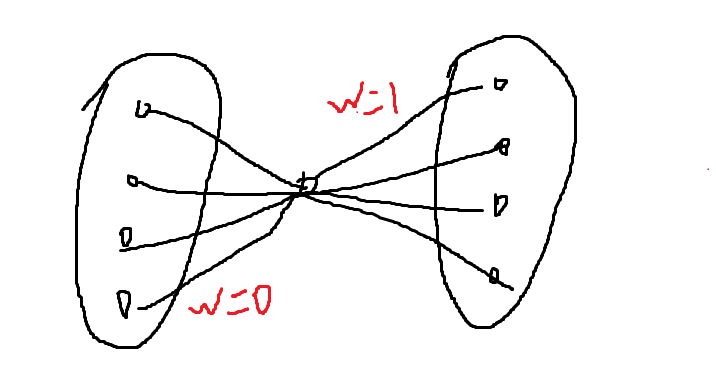
同时，对于本题，把未停靠的站点和停靠的分成两个集合，那么需要连边最坏情况下是要\(n^2\)，考虑最坏情况下，一共有\(1000\)趟车，每一趟都是从1~n站，其中停靠了\(500\)个站，还有\(500\)个未停靠，那么这时候连边就是\(500 * 500 * 1000 = 250000000\)，显然，复杂度爆炸，但是考虑一种优化，在集合中间建立虚拟结点，左边边权是\(0\)，右边边权是\(1\)，那么就优化成了\(O(n + m)\)连边方式了，再算一下最坏情况下的数据量，\((500 + 500) * 1000 = 1000000\)，这样就可以过了，直接优化成了线性，并且完全等价于\(O(n^2)\)连边的方式。

// Problem: 车站分级
// Contest: AcWing
// URL: https://www.acwing.com/problem/content/458/
// Memory Limit: 64 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)

#include <bits/stdc++.h>

using namespace std;

const int N = 2010, M = 1E6 + 10;

int h[N], e[M], ne[M], w[M], idx;
int n, m;
int d[N];
int dist[N];
int seq[N], cnt;
bool st[N];

void add(int a, int b, int c) {
	e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
	d[b]++;
}

void topsort() {
	queue<int> q;
	for (int i = 1; i <= n + m; i++) {
		if (!d[i]) q.push(i);
	}

	while (q.size()) {
		int t = q.front();
		q.pop();	

		seq[cnt++] = t;

		for (int i = h[t]; ~i; i = ne[i]) {
			int j = e[i];
			if (--d[j] == 0) q.push(j);
		}
	}
}

int main() {
	scanf("%d%d", &n, &m);
	memset(h, -1, sizeof h);
	for (int i = 1; i <= m; i++) {
		int cnt;
		scanf("%d",  &cnt);
		memset(st, 0, sizeof st);
		int start = n, end = 1;
		while (cnt--) {
			int k;
			scanf("%d", &k);
			start = min(start, k);
			end = max(end, k);
			st[k] = true;
		}	

		int vir = n + i;
		for (int j = start; j <= end; j++) {
			if (!st[j]) add(j, vir, 0);
			else add(vir, j, 1);
		}
	}

	topsort();

	for (int j = 1; j <= n; j++) dist[j] = 1;
	for (int j = 0; j < n + m; j++) {
		int var = seq[j];
		for (int k = h[var]; ~k; k = ne[k]) {
			dist[e[k]] = max(dist[e[k]], dist[var] + w[k]);
		}
	}

	int res = 0;
	for (int i = 1; i <= n; i++) res = max(res, dist[i]);
	printf("%d\n", res);

    return 0;
}