预处理共轭梯度算法(Preconditioned Conjugate Gradients Method)的代码实现

前文：

预处理共轭梯度算法(Preconditioned Conjugate Gradients Method)

给出代码：

import numpy as np
# from rllab.misc.ext import sliced_fun
EPS = np.finfo('float64').tiny
def cg(f_Ax, b, cg_iters=10, callback=None, verbose=False, residual_tol=1e-10):
    """
    Demmel p 312
    """
    p = b.copy()
    r = b.copy()
    x = np.zeros_like(b)
    rdotr = r.dot(r)
    fmtstr = "%10i %10.3g %10.3g"
    titlestr = "%10s %10s %10s"
    if verbose: print(titlestr % ("iter", "residual norm", "soln norm"))
    for i in range(cg_iters):
        if callback is not None:
            callback(x)
        if verbose: print(fmtstr % (i, rdotr, np.linalg.norm(x)))
        z = f_Ax(p)
        v = rdotr / p.dot(z)
        x += v * p
        r -= v * z
        newrdotr = r.dot(r)
        mu = newrdotr / rdotr
        p = r + mu * p
        rdotr = newrdotr
        if rdotr < residual_tol:
            break
    if callback is not None:
        callback(x)
    if verbose: print(fmtstr % (i + 1, rdotr, np.linalg.norm(x)))  # pylint: disable=W0631
    return x
def preconditioned_cg(f_Ax, f_Minvx, b, cg_iters=10, callback=None, verbose=False, residual_tol=1e-10):
    """
    Demmel p 318
    """
    x = np.zeros_like(b)
    r = b.copy()
    p = f_Minvx(b)
    y = p
    ydotr = y.dot(r)
    fmtstr = "%10i %10.3g %10.3g"
    titlestr = "%10s %10s %10s"
    if verbose: print(titlestr % ("iter", "residual norm", "soln norm"))
    for i in range(cg_iters):
        if callback is not None:
            callback(x, f_Ax)
        if verbose: print(fmtstr % (i, ydotr, np.linalg.norm(x)))
        z = f_Ax(p)
        v = ydotr / p.dot(z)
        x += v * p
        r -= v * z
        y = f_Minvx(r)
        newydotr = y.dot(r)
        mu = newydotr / ydotr
        p = y + mu * p
        ydotr = newydotr
        if ydotr < residual_tol:
            break
    if verbose: print(fmtstr % (cg_iters, ydotr, np.linalg.norm(x)))
    return x
def test_cg():
    A = np.random.randn(5, 5)
    A = A.T.dot(A)
    b = np.random.randn(5)
    x = cg(lambda x: A.dot(x), b, cg_iters=5, verbose=True)  # pylint: disable=W0108
    assert np.allclose(A.dot(x), b)
    x = preconditioned_cg(lambda x: A.dot(x), lambda x: np.linalg.solve(A, x), b, cg_iters=5,
                          verbose=True)  # pylint: disable=W0108
    assert np.allclose(A.dot(x), b)
    x = preconditioned_cg(lambda x: A.dot(x), lambda x: x / np.diag(A), b, cg_iters=5,
                          verbose=True)  # pylint: disable=W0108
    assert np.allclose(A.dot(x), b)
def lanczos(f_Ax, b, k):
    """
    Runs Lanczos algorithm to generate a orthogonal basis for the Krylov subspace
    b, Ab, A^2b, ...
    as well as the upper hessenberg matrix T = Q^T A Q
    from Demmel ch 6
    """
    assert k > 1
    alphas = []
    betas = []
    qs = []
    q = b / np.linalg.norm(b)
    beta = 0
    qm = np.zeros_like(b)
    for j in range(k):
        qs.append(q)
        z = f_Ax(q)
        alpha = q.dot(z)
        alphas.append(alpha)
        z -= alpha * q + beta * qm
        beta = np.linalg.norm(z)
        betas.append(beta)
        print("beta", beta)
        if beta < 1e-9:
            print("lanczos: early after %i/%i dimensions" % (j + 1, k))
            break
        else:
            qm = q
            q = z / beta
    return np.array(qs, 'float64').T, np.array(alphas, 'float64'), np.array(betas[:-1], 'float64')
def lanczos2(f_Ax, b, k, residual_thresh=1e-9):
    """
    Runs Lanczos algorithm to generate a orthogonal basis for the Krylov subspace
    b, Ab, A^2b, ...
    as well as the upper hessenberg matrix T = Q^T A Q
    from Demmel ch 6
    """
    b = b.astype('float64')
    assert k > 1
    H = np.zeros((k, k))
    qs = []
    q = b / np.linalg.norm(b)
    beta = 0
    for j in range(k):
        qs.append(q)
        z = f_Ax(q.astype('float64')).astype('float64')
        for (i, q) in enumerate(qs):
            H[j, i] = H[i, j] = h = q.dot(z)
            z -= h * q
        beta = np.linalg.norm(z)
        if beta < residual_thresh:
            print("lanczos2: stopping early after %i/%i dimensions residual %f < %f" % (j + 1, k, beta, residual_thresh))
            break
        else:
            q = z / beta
    return np.array(qs).T, H[:len(qs), :len(qs)]
def make_tridiagonal(alphas, betas):
    assert len(alphas) == len(betas) + 1
    N = alphas.size
    out = np.zeros((N, N), 'float64')
    out.flat[0:N ** 2:N + 1] = alphas
    out.flat[1:N ** 2 - N:N + 1] = betas
    out.flat[N:N ** 2 - 1:N + 1] = betas
    return out
def tridiagonal_eigenvalues(alphas, betas):
    T = make_tridiagonal(alphas, betas)
    return np.linalg.eigvalsh(T)
def test_lanczos():
    np.set_printoptions(precision=4)
    A = np.random.randn(5, 5)
    A = A.T.dot(A)
    b = np.random.randn(5)
    f_Ax = lambda x: A.dot(x)  # pylint: disable=W0108
    Q, alphas, betas = lanczos(f_Ax, b, 10)
    H = make_tridiagonal(alphas, betas)
    assert np.allclose(Q.T.dot(A).dot(Q), H)
    assert np.allclose(Q.dot(H).dot(Q.T), A)
    assert np.allclose(np.linalg.eigvalsh(H), np.linalg.eigvalsh(A))
    Q, H1 = lanczos2(f_Ax, b, 10)
    assert np.allclose(H, H1, atol=1e-6)
    print("ritz eigvals:")
    for i in range(1, 6):
        Qi = Q[:, :i]
        Hi = Qi.T.dot(A).dot(Qi)
        print(np.linalg.eigvalsh(Hi)[::-1])
    print("true eigvals:")
    print(np.linalg.eigvalsh(A)[::-1])
    print("lanczos on ill-conditioned problem")
    A = np.diag(10 ** np.arange(5))
    Q, H1 = lanczos2(f_Ax, b, 10)
    print(np.linalg.eigvalsh(H1))
    print("lanczos on ill-conditioned problem with noise")
    def f_Ax_noisy(x):
        return A.dot(x) + np.random.randn(x.size) * 1e-3
    Q, H1 = lanczos2(f_Ax_noisy, b, 10)
    print(np.linalg.eigvalsh(H1))
if __name__ == "__main__":
    test_lanczos()
    test_cg()

上面的cg函数是共轭梯度法，preconditioned_cg函数是预处理共轭梯度法。

可以看到，预处理的共轭梯度法和共轭梯度法是比较相似的，下面给出不同的地方：

共轭梯度法：

        newrdotr = r.dot(r)
        mu = newrdotr / rdotr
        p = r + mu * p
        rdotr = newrdotr

预处理共轭梯度法：

        y = f_Minvx(r)
        newydotr = y.dot(r)
        mu = newydotr / ydotr
        p = y + mu * p
        ydotr = newydotr

上面的代码中给出的对预处理共轭梯度法的两次调用：

    x = preconditioned_cg(lambda x: A.dot(x), lambda x: np.linalg.solve(A, x), b, cg_iters=5,
                          verbose=True)  # pylint: disable=W0108
    assert np.allclose(A.dot(x), b)
    x = preconditioned_cg(lambda x: A.dot(x), lambda x: x / np.diag(A), b, cg_iters=5,
                          verbose=True)  # pylint: disable=W0108
    assert np.allclose(A.dot(x), b)

运行结果：

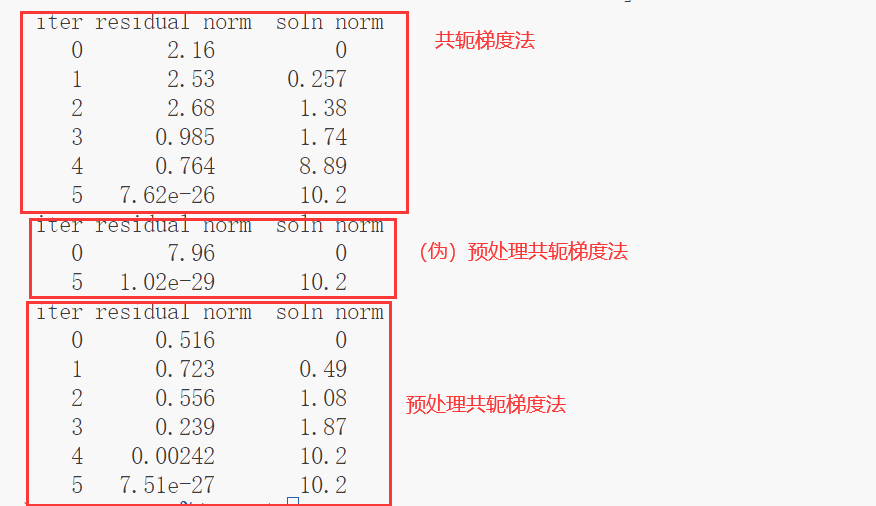
之所以说第一个预处理共轭梯度法是一个伪的呢，是因为其预处理依旧是使用求解A矩阵的解，因此并不具备实际意义和价值。

下图来自：预处理共轭梯度法（2）

可以看到上面代码中的预处理共轭梯度法其实就是使用Jacobi方法的，主要体现：

lambda x: x / np.diag(A)

由于预处理共轭梯度法比共轭梯度法的优势在于对稀疏的系数矩阵且系数矩阵的条件数(最大最小特征值之比)很大的情况，因此上面的Jacobi方法的预处理共轭梯度法并没有明显的优势。