Burnside 定理

Burnside 定理

问题：

给定一个 \(n\) 个点，\(n\) 条边的环，有 \(m\) 种颜色，给每个顶点染色，问有多少种本质不同的染色方案，答案对 \(10^9+7\) 取模

注意本题的本质不同，定义为：只需要不能通过旋转与别的染色方案相同。

题目初步解读

我们考虑如果不要求本质不同只需要 \(n^n\) 。

但因为无标号的环就会重复。

例如这是一个 4 个点， 2 种颜色的情况：

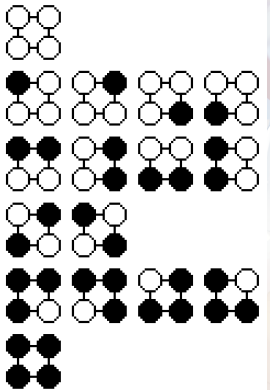
在这里面如果不要求本质不同就有 16 种方案，若要求，则只有 6 种。

同一行的都是一种方案。

Burnside 引入

我们先来一些定义

置换群

令集合 \(N=\{1,2,\cdots,n\}\) 。

令集合 \(M\) 为 \(N\) 若干个排列构成的集合。

令群 \(G = (M,\times)\) 其中符号 \(\times\) 解释如下：

\(\sigma\) 是一个排列，也就是 \(M\) 周一个元素。

写为 \(\sigma \times a\) 不过更习惯被表示为 \(\sigma(a)\) 。

其运算规则为：\(\sigma(a)= (a_{\sigma_1},a_{\sigma_2}...a_{\sigma_n})\)。

在前面样例中，置换群是：

\((\{\)旋转\(0°,\)旋转\(90°,\)旋转\(180°,\)旋转\(270° \},\times)\)

若写成排列则是：

\((\{\{1,2,3,4\},\{2,3,4,1\},\{3,4,1,2\},\{4,1,2,3\}\},\times)\)

轨道

考虑一个作用在 \(X\) 上的置换群 \(G\) ， \(X\) 中一个元素 \(x\) 的轨道则是 \(x\) 通过 \(G\) 中元素可以转移到的元素的集合。记作 \(G(x)\) 。

样例中每一行就是一个轨道。例如下面就是一个轨道。

稳定子

稳定子定义为：\(G^x = \{g|g\in G,g \times x = x\}\)。

使用语言描述，便是群 \(G\) 中满足 \(g(x)=x\) 的所有元素 \(g\) 所构成的集合。

样例中：

的稳定子为 \(\{\)旋转\(0°\}\)，

的稳定子为 \(\{\)旋转\(0°,\)旋转\(180°\}\)，

的稳定子为 \(\{\)旋转\(0°,\)旋转\(90°,\)旋转\(180°,\)旋转\(270°\}\)。

轨道-稳定子定理：

我们可以发现：

1.在同一轨道的元素稳定子个数一定相等。

2.稳定子大小乘轨道大小等于群 \(G\) 大小。

\[|G^x|\times |G(x)|=|G|
\]

没错，他是个定理，考虑感性证明：

一个元素 \(x\) 按照 \(G\) 的操作一定可以得到轨道内所有元素，也就是集合 \(G(x)\) 。

但在操作过程中会有重复的，重复的次数也就是稳定子集合大小。

详细证明可以看这里。

不动点

若 \(g(x) = x\) 则称 \(x\) 是在 \(g\) 下的不动点。

定义集合 \(X^g = \{x|g(x) = x,x\in X\}\)。

稳定子和不动点有类似反演的关系。

若 x 的稳定子集合里有 \(g\)，那么 g 下不动点集合中也有 x。

所以对于每一个 \(x\) 稳定子的个数之和等于对于每一个 \(g\) 不动点个数之和。

形式化

\[\sum_{x\in X} {|G(x)|} = \sum_{g\in G} |X^g|
\]

注意稳定子是对于 g 来说的，而不动点是对于 x 来说的。

例如 ''旋转180°'' 不动点是

Burnside 定理

公式：

我们要求的答案一般来说也就是轨道数量。

\[ans = \dfrac{1}{|G|}\sum_{g\in G} X^g
\]

证明：

等价类数量也就是轨道数量。

\(|G(x)|\) 代表 \(x\) 所在轨道大小。

\[ans = \sum_{x\in X} \frac 1 {|G(x)|}
\]

根据轨道-稳定子定理得

\[ans = \sum_{x\in X} \frac {|G^x|}{|G|}=\frac 1 {|G|} \sum_{x\in X} {|G^x|}
\]

用稳定子和不动点关系得：

\[ans = \dfrac{1}{|G|}\sum_{g\in G} |X^g|
\]

回到题目

扩展到 \(n\)，现在的 \(G\) 就是\(\{\) 旋转 \(0\) 次，旋转 \(1\) 个，\(\cdots\)，旋转\(n-1\)个 \(\}\)。

考虑旋转 \(k\) 次的不动点个数是 \(n^{\gcd(k,n)}\)。

当 \(\gcd(k,n) = k\):

我们按照 \(k\) 将环切成 \(\frac n k\) 份，然后标上号。

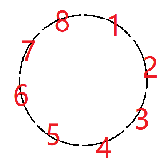
将他旋转。

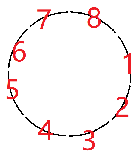
我们发现每一份必须一样他才是个不动点。

答案就是 \(n^k = n^{\gcd(n,k)}\)。

当 \(gcd(k,n) \ne k\):

令 \(g = \gcd(k,n)\) 那么我们将他旋转 \(g \times \frac k g\) ，等价于将长度为 \(g\) 的旋转 \(\frac k g\) 次。

答案就是 \(n^{gcd(n,k)}\)。

如果还不懂，建议手模一下 \(k = 4,n = 6\) 这个样例。

应用Burnside则有

\[Ans = \dfrac{1}{n}\sum_{k=1}^{n} n^{\gcd(k,n)}
\]

发现有 \(\gcd\) ，可以莫反。

莫反基操，不多说。

\[\frac{1}{n}\sum_{d|n}n^d \varphi(\frac{n}{d})
\]

直接暴力可过。

Pólya 定理

就是染色问题中Burnside的运用。

对于一个排列 \(g\) ，我们将每一个 \(i\) 向 \(a_i\) 连一条边，会得到若干环，每个环内元素颜色应该相同。定义 \(c(g)\) 代表环数量，那么 Pólya 就是

\[\dfrac{1}{|G|}\sum_{g\in G}m^{c(g)}
\]