Ex 6_20 最优二叉搜索树..._第六次作业

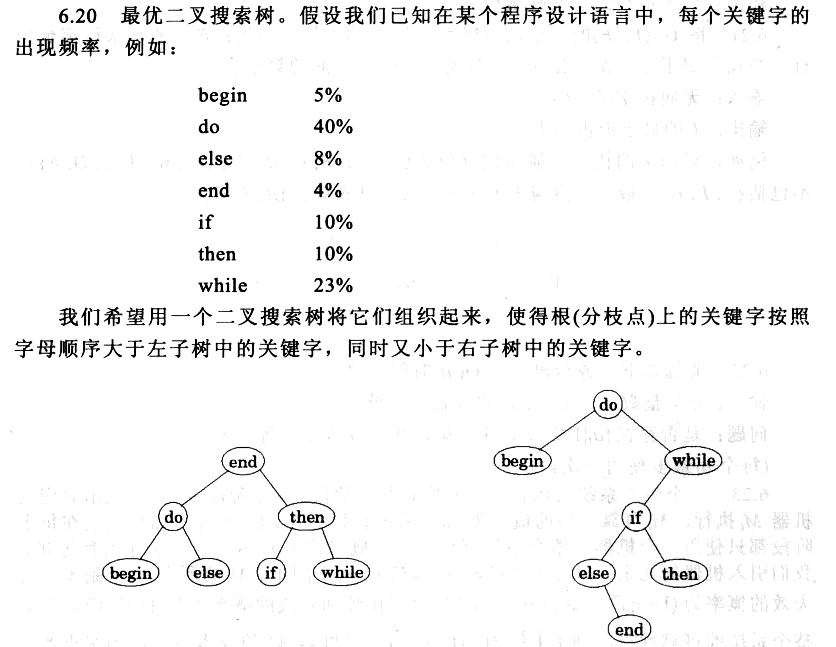
假设关键字的总数为n，用c[i,j]表示第i个关键字到第j个关键字的最优二叉查找树的代价，我们的目标是求c[0,n-1]。要求c[i,j],首先要从第i个关键字到第j个关键字中选一个出来作为根结点，选出根结点后，最优二叉搜索树的代价为左子树的代价加上右子树的代价，由于每选出一个根结点，每个关键字的搜索长度都增加1，因此得出递推式，即当

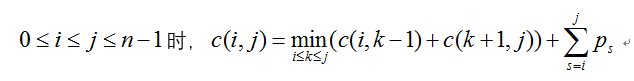
 package org.xiu68.ch06.ex6;

 public class Ex6_20 {
     //动态规划，最优二叉搜索树
     public static void main(String[] args) {
         // TODO Auto-generated method stub
         double[] w=new double[]{0.05,0.4,0.08,0.04,0.1,0.1,0.23};
         String[] words=new String[]{"begin","do","else","end","if","then","while"};
         int[][] roots=new int[w.length][w.length];        //i到j之间的二叉搜索树的根结点
         optimalBST(w,roots);

         for(int i=0;i<roots.length;i++){
             for(int j=0;j<roots[i].length;j++){
                 System.out.print(roots[i][j]+"\t");
             }
             System.out.println();
         }

         printRoot(words, roots,0,w.length-1);
         /*
          最少平均比较次数为：2.18
         0    1    1    1    1    1    1
         0    1    1    1    1    1    4
         0    0    2    2    4    4    6
         0    0    0    3    4    4    6
         0    0    0    0    4    4    6
         0    0    0    0    0    5    6
         0    0    0    0    0    0    6
         begin和while的根结点为 do
         begin和begin的根结点为 begin
         else和while的根结点为 while
         else和then的根结点为 if
         else和end的根结点为 else
         end和end的根结点为 end
         then和then的根结点为 then
         */
     }

     //roots中存放i到j之间的二叉搜索树的根结点
     public static void optimalBST(double[] w,int[][] roots){
         double[][] c=new double[w.length][w.length];    //i到j之间的二叉搜索树的最小代价

         for(int i=0;i<w.length;i++){
             c[i][i]=w[i];        //树只有自身，则代价为自身的频率
             roots[i][i]=i;        //(i到j的树的根结点)自身作为根结点
         }

         for(int s=2;s<=w.length;s++){            //s个单词作为子问题(子问题的规模)
             for(int i=0;i<=w.length-s;i++){        //s个单词的第一个单词
                 int j=i+s-1;                    //s个单词的最后一个单词

                 double min=Double.MAX_VALUE;
                 for(int k=i;k<=j;k++){            //寻找使平均查找次数最少的根结点
                     double cLeft=0;                //以k作为根结点的左子树的代价
                     double cRight=0;            //以k作为根结点的右子树的代价
                     if(k>i)
                         cLeft=c[i][k-1];
                     if(k<j)
                         cRight=c[k+1][j];
                     if(cLeft+cRight<min){
                         min=cLeft+cRight;
                         roots[i][j]=k;
                     }
                 }//
                 double sum=0;
                 for(int t=i;t<=j;t++){
                     sum+=w[t];
                 }
                 c[i][j]=min+sum;
             }//
         }//
         System.out.println("最少平均比较次数为："+c[0][w.length-1]);
     }

     //打印最优根
     public static void printRoot(String[] words,int[][] roots,int i,int j){
         if(i<=j){
             int k=roots[i][j];
             System.out.println(words[i]+"和"+words[j]+"的根结点为 "+words[k]);
             printRoot(words,roots,i,k-1);
             printRoot(words,roots,k+1,j);
         }
     }
 }