vue自学入门-2（vue创建项目）
本人也是刚学习VUE，边找资料，边学习，边给大家分享。
1、创建项目
2、启动项目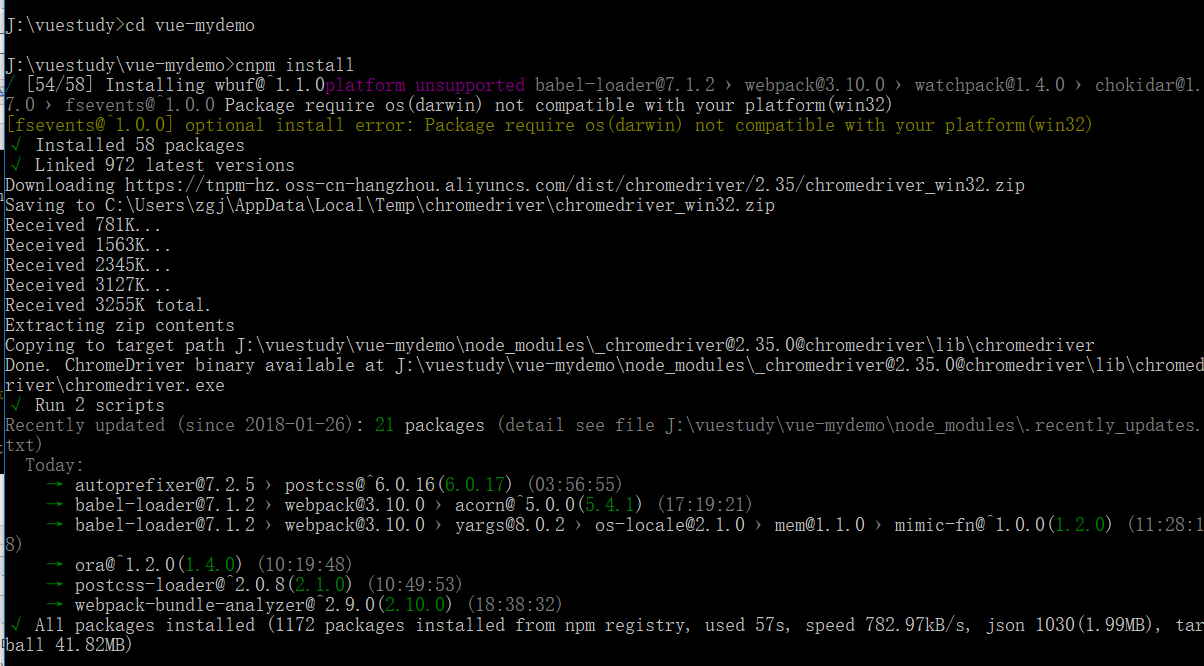
3、注意上面和下面全部用cnpm
vue自学入门-2（vue创建项目）的更多相关文章
- vue自学入门-6（vue jsx）
目录: vue自学入门-1(Windows下搭建vue环境) vue自学入门-2(vue创建项目) vue自学入门-3(vue第一个例子) vue自学入门-4(vue slot) vue自学入门-5( ...
- vue自学入门-4（vue slot）
vue自学入门-1(Windows下搭建vue环境) vue自学入门-2(vue创建项目) vue自学入门-3(vue第一个例子) vue自学入门-4(vue slot) vue自学入门-5(vuex ...
- vue自学入门-5（vuex state）
vue自学入门-1(Windows下搭建vue环境) vue自学入门-2(vue创建项目) vue自学入门-3(vue第一个例子) vue自学入门-4(vue slot) vue自学入门-5(vuex ...
- vue自学入门-7（vue style scope）
vue自学入门-1(Windows下搭建vue环境) vue自学入门-2(vue创建项目) vue自学入门-3(vue第一个例子) vue自学入门-4(vue slot) vue自学入门-5(vuex ...
- vue自学入门-8（vue slot-scope）
vue自学入门-1(Windows下搭建vue环境) vue自学入门-2(vue创建项目) vue自学入门-3(vue第一个例子) vue自学入门-4(vue slot) vue自学入门-5(vuex ...
- vue 快速入门 系列 —— Vue(自身) 项目结构
其他章节请看: vue 快速入门 系列 Vue(自身) 项目结构 前面我们已经陆续研究了 vue 的核心原理:数据侦测.模板和虚拟 DOM,都是偏底层的.本篇将和大家一起来看一下 vue 自身这个项目 ...
- vue 快速入门 系列 —— vue 的基础应用（上）
其他章节请看: vue 快速入门 系列 vue 的基础应用(上) Tip: vue 的基础应用分上下两篇,上篇是基础,下篇是应用. 在初步认识 vue一文中,我们已经写了一个 vue 的 hello- ...
- vue 快速入门 系列 —— vue loader 上
其他章节请看: vue 快速入门 系列 vue loader 上 通过前面"webpack 系列"的学习,我们知道如何用 webpack 实现一个不成熟的脚手架,比如提供开发环境和 ...
- vue 快速入门 系列 —— vue loader 下
其他章节请看: vue 快速入门 系列 vue loader 下 CSS Modules CSS Modules 是一个流行的,用于模块化和组合 CSS 的系统.vue-loader 提供了与 CSS ...
- vue 快速入门 系列 —— vue loader 扩展
其他章节请看: vue 快速入门 系列 vue loader 扩展 在vue loader一文中,我们学会了从零搭建一个简单的,用于单文件组件开发的脚手架.本篇将在此基础上继续引入一些常用的库:vue ...
随机推荐
- Docker 安装私有镜像库的简单使用
公司的网络实在是太差了, 想着自己搭建一个私有的镜像库进行使用测试使用.... docker pull registry.docker-cn.com/library/registry docker t ...
- python常用命令和基础运算符
基础运算符 http://www.cnblogs.com/alex3714/articles/5465198.html 身份运算符:is is not成员运算符:in not in ##in 判断元素 ...
- python之发送HTML内容的邮件
# 发送html内容的邮件 import smtplib, time, os from email.mime.text import MIMEText from email.header import ...
- PHP生成二维码并上传到七牛云
参考资料 qr-code生成二维码 七牛云上传图片 实现步骤 //拿到插入后的id $res = DB::table('book_book')->insertGetId($data); i ...
- Qtree3题解（树链剖分+线段树+set）
外话:最近洛谷加了好多好题啊...原题入口 这题好像是SPOJ的题,挺不错的.看没有题解还是来一篇... 题意 很易懂吧.. 题解 我的做法十分的暴力:树链剖分(伪)+线段树+ std :: set ...
- Python解惑：整数比较
在 Python 中一切都是对象,毫无例外整数也是对象,对象之间比较是否相等可以用==,也可以用is.==和is操作的区别是: is比较的是两个对象的id值是否相等,也就是比较俩对象是否为同一个实例对 ...
- Centos7下Zabbix3.4至Zabbix4.0的升级步骤
点击返回:自学Zabbix之路 点击返回:自学Zabbix4.0之路 点击返回:自学zabbix集锦 Centos7下Zabbix3.4至Zabbix4.0的升级步骤 查看现在centos版本和zab ...
- BZOJ5298 [CQOI2018] 交错序列 | 矩阵乘法和一个trick
题面 求所有长度为\(n\)的.没有相邻的1的01序列中,若0有\(x\)个.1有\(y\)个,\(x^ay^b\)之和(对\(m\)取模). \(n \le 10^7, m \le 10^8, 0 ...
- 更新本地git仓库的远程地址（remote地址）
如果远程仓库的地址更新了,我们本地仓库就需要更新remote地址, 可以通过git remote -v或者cat .git/config查看通信方式及远程地址 更新远程地址的方式有两种: 第一种方式: ...
- 51nod1237 最大公约数之和 V3
题意:求 解: 最后一步转化是因为phi * I = Id,故Id * miu = phi 第二步是反演,中间省略了几步... 然后就这样A了......最终式子是个整除分块,后面用杜教筛求一下phi ...