koa01

1、koa简介

koa是express团队开发的一个更加轻量级的服务端开发框架，也是未来的趋势

2、安装

npm i -g koa-generator //全局安装koa脚手架

3、创建项目

koa2 项目名称

例如：koa2 -e koa2-learn //e的意思是使用ejs模板引擎，要不默认jade

将为我们创建一个koa-learn目录

接下来进入该目录，根据提示执行cnpm i

可能需要进行2次安装，看提示有无Pass --update-binary...

复制DEBUG...代码，运行koa

在package.json文件中可以修改启动方式：

npm run dev可以实现修改过程中的监听

端口默认运行在3000

4、

koa中的全局变量被称为global而不是window

5、koa异步，es6异步语法

async(param)=>{

await ... //只有在有声明async的方法内才准使用await

}

解决回调地狱，我们可以使用Promise,也可以使用await

举例分析：

const a=await A
const b=await B
const c=await C

上述代码为伪代码，ABC是不同的异步操作

在A未执行完成前不会执行下一行代码，以此类推

相当于用同步的写法完成了异步的过程

这里的ABC就是Promise对象，如果不是promise对象将自动转换，即Promise.resolve(data)

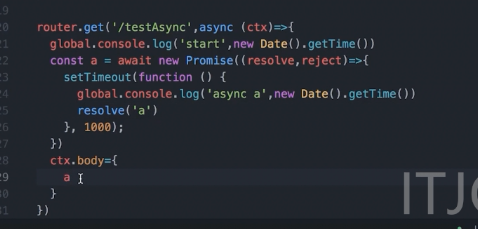
正确执行promise过程后的传给resolve的data将被赋值给a

6、koa2中间件

const+require引入中间件。通过app.use声明使用

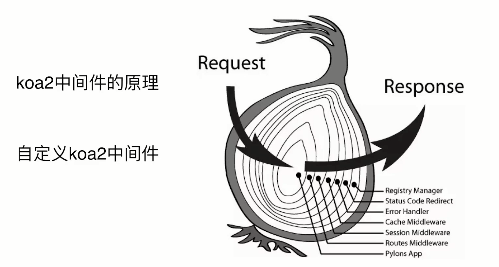
引用时按顺序，使用时没有顺序

中间件都会被经过两次

一个简单的中间件编写：

function pv(ctx){
    //ctx是一个全局对象，挂载了request和response的信息
    global.console.log(ctx.path)

    module.export=function(){
        return async function(ctx,next){
            pv(ctx)
            await next()//pv中间件处理完毕，准许移交下一个中间件处理
        }
    }
}

　　使用时，在app.js中书写：

const pv=require('./middleware/koa-pv')

app.use(pv())

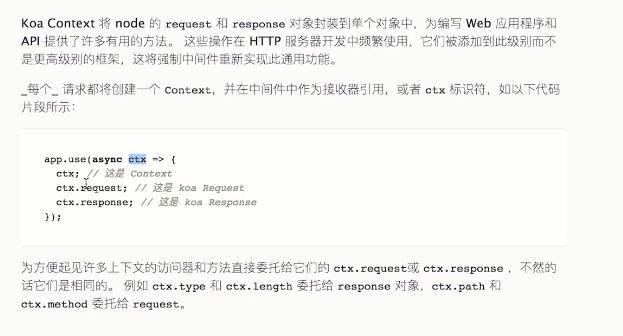
保证了两次交互。

8、koa-router 的用法：

根据子域名不同可配置不同的路由文件：

body属性返回相应的一些数据，可以返回多种类型：字符串，json等

render方法返回一个页面

const router =require('koa-router')

router.prefix('./user')

9、koa读写cookie

ctx.get/ctx.set