奈奎斯特采样定理（Nyquist）

采样定理在1928年由美国电信工程师H.奈奎斯特首先提出来的，因此称为奈奎斯特采样定理。

1933年由苏联工程师科捷利尼科夫首次用公式严格地表述这一定理，因此在苏联文献中称为科捷利尼科夫采样定理。

1948年信息论的创始人C.E.香农对这一定理加以明确地说明并正式作为定理引用，因此在许多文献中又称为香农采样定理。

奈奎斯特采样定理解释了采样率和所测信号频率之间的关系。 阐述了采样率fs必须大于被测信号感兴趣最高频率分量的两倍。

该频率通常被称为奈奎斯特频率f_N。即：

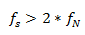
首先，我们要明确以下两点：

• 采样的目的是为了利用有限的采用率，无失真的还原出原有声音信号的样子。
• 奈奎斯特采样定理也可以理解为一个正弦波每个周期最少取两个点才能把正弦波还原回去。

为更好理解其原因，让我们来看看不同速率测量的正弦波。

1. 假设  f_S  = f_N 

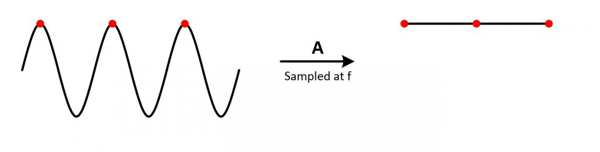
可以看出，无论我们从哪一点开始采样，每次采集到的数据都是一样的，对应的频率成分为0Hz。

2. 假设 f_S = (4/ 3) * f_N 

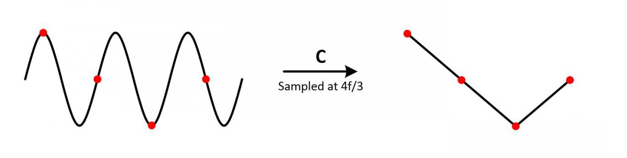
以上采样到的曲线仍然无法还原原有波形的样子。

3. 假设 f_S  = 2 * f_N 

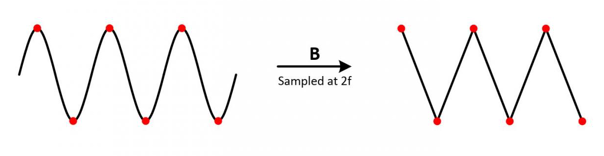
如上图，将这些采样点连成线条，得到的信号形状为三角波，虽然信号的频率成分没有失信，但是很难保证信号的幅值不失真。因为这两个采样点很难位于正弦信号的波峰与波谷处。也就是说，在很大程度上，采样后的信号的幅值是失真的。

我们再考虑如下情况：

假设一条正弦曲线为sin(2π/t)，频率为1Hz。我们以2Hz的频率对该曲线进行采样（每隔0.5s），可以得到3个红色采样数据，如下图：

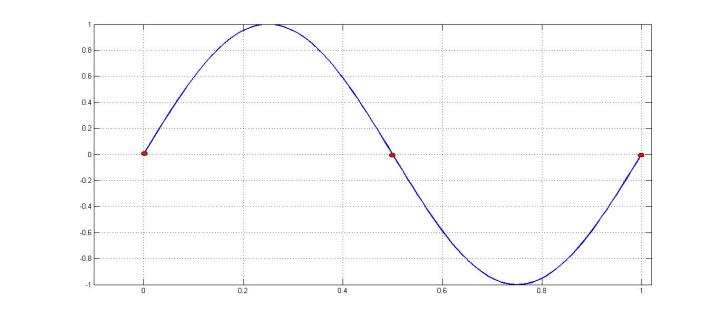
对于这三个点，我们不能确定它对应的正弦曲线是sin(2π/t)，因为sin(4π/t)等倍频曲线也会穿过这三个红色采样点：

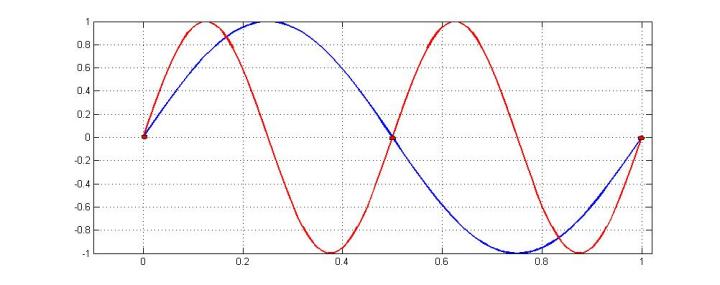
混叠

如果信号的采样率低于两倍奈奎斯特频率，采样数据中就会出现虚假的低频成分。 这种现象便称为混叠。

下图显示了800 kHz正弦波1MS/s时的采样。虚线表示该采样率时记录的混叠信号。 800 kHz频率与通带混叠，错误地显示为200 kHz正弦波。

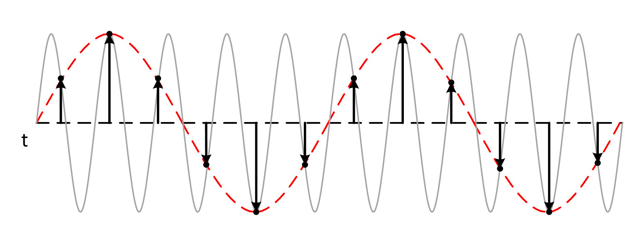
绝大多数信号都是能够进行傅里叶变换的，就意味着，不管一个信号多么复杂，总可以分解为若干个正（余）弦信号的和，对应了信号的频率分量。因此，Nyquist采样定理只需找到信号最大的频率分量，再用2倍于最大频率分量的采样频率对信号进行采样，从理论上解决了，离散信号能够重建出连续信号的问题。