【LeetCode回溯算法#01】图解组合问题

组合问题

力扣题目链接(opens new window)

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

示例:

输入: n = 4, k = 2

输出:

[

[2,4],

[3,4],

[2,3],

[1,2],

[1,3],

[1,4],

]

思路

如果像题目给的例子那样，k是一个较小的值（比如2），那么一个很直接的想法是使用两层for循环去遍历数组即可

vector<vector<int>> res;
vector<int> temp;
for(int i = 0; i < n; ++i){
    for(int j = i; j < n; ++j){
        temp.push_back(i);
        temp.push_back(j);
        res.push_back(temp);
        temp.clear();
    }
}
return res;

那如果k要是100呢？写100层for循环？

显然，使用for循环进行暴力遍历的话，遍历的深度是有限的

既然涉及到了深度，那么递归和树结构就很适合来解决此类问题了

首先，递归可以在设置的条件范围内搜索到足够的深度，我们实际上只用在递归的最后一层进行横向遍历（即for循环），其余的则在回溯过程中处理

其次，我们可以将整个搜索过程想象成一个树结构

当我们通过递归到达某个分支的"叶子结点"后，这条路径上保存的节点值就是一个组合的结果

下面贴一下卡哥的图和我经过理解补充的图，可以对比来看方便理解

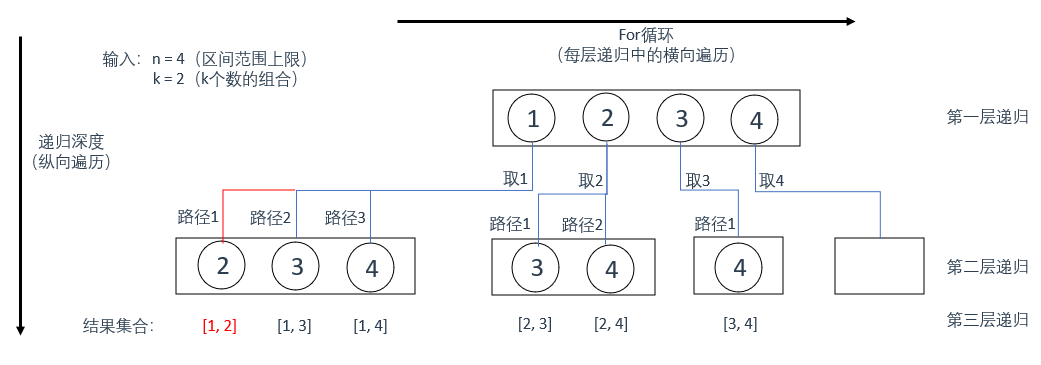
可以看到，每层递归中都有一个for循环，目的是用于处理本层递归的横向遍历过程

当第一层递归被调用时，其中的for循环会依次处理[1,2,3,4]，取1（将1保存）

此时又触发一层递归，第二层递归会依次处理[2,3,4]，取2（将2保存）

此时，再次触发递归，到达第三层，在第三层递归中，我们判定用于保存结果的数组（目前为[1,2]）的大小已经等于k值

因此，在第三层递归中触发了终止条件，递归结束

回溯，到达第二层递归，此时将结果数组中的2弹出

回溯，到达第一层递归，此时将结果数组中的1弹出

第一层递归中的for继续遍历到下一个数（即2），然后重复上述递归过程

当然，在第二层递归中，每次起始的遍历位置是不同的，后面代码里会解释

代码分析

写递归嘛，那还是遵循递归的步骤，但这里其实可以改叫回溯三部曲了

1、确定递归函数的返回值和参数

本质上我们是使用递归去操作/遍历一个数组，因此不需要返回值

输入参数那肯定是遍历区间n和组合大小k了

经过上面的分析得知，我们还需要一个数组来保存每层递归取到的结果

这里将该数组命名为path，其记录的是我们从第一层递归到最里层递归这条路径上遇到并保存的值

还需要一个数组res来保存所有的path

并且，在第二层递归中，为了防止组合中出现重复值（[1,2]和[2,1]被视为相同结果），我们需要不断调整遍历的范围

因此输入参数中还需要一个变量给出遍历的起始位置

class Solution {
public:
   	//定义数组
    vector<int> path;
    vector<vector<int>> res;//保存最终结果
    void backtracking(int n, int k, int beginIndex){

    }

    vector<vector<int>> combine(int n, int k) {

    }
};

2、确定终止条件

还是通过前面的讨论得知，当我们到达最里层递归时，需要终止。即到达我们想象的二叉树结果的叶子节点

如何判断"到达叶子节点"这件事呢？

其实可以通过路径数组path的大小来判断，如果path的大小等于k，说明递归的深度已经到头了，此时应该结束递归

class Solution {
public:
   	//定义数组
    vector<int> path;
    vector<vector<int>> res;//保存最终结果
    void backtracking(int n, int k, int beginIndex){
        //确定终止条件
        if(path.size() == k){
            //保存path到res
			res.push_back(path);
            return;//结束递归
        }
    }

    vector<vector<int>> combine(int n, int k) {

    }
};

3、确定单层处理逻辑

这一部分需要去规定在本层递归中应该如何遍历数组

还是结合前面的分析：我们在一层递归中实际需要做的是使用for对当前以beginIndex为起始，以n为结束（即[beginIndex, n]）的数组进行遍历

那就写for循环呗

class Solution {
public:
   	//定义数组
    vector<int> path;
    vector<vector<int>> res;//保存最终结果
    void backtracking(int n, int k, int beginIndex){
        //确定终止条件
        if(path.size() == k){
            //保存path到res
			res.push_back(path);
            return;//结束递归
        }

        //确定单层处理逻辑
        //遍历本层递归的数组，范围是[beginIndex, n]
        for(int i = beginIndex; i < n; ++i){
            //添加当前路径节点值到path
            path.push_back(i);
            //进入下一层递归
            backtracking(int n, int k, i + 1);//跳过当前值
            //编写回溯处理逻辑
            //回溯时删掉当前层保存的值
            path.pop_back();
        }
    }
    vector<vector<int>> combine(int n, int k) {

    }
};

打完收工

完整代码

在主函数中，把backtracking调用并给出beginIndex的初值即可

class Solution {
public:
   	//定义数组
    vector<int> path;
    vector<vector<int>> res;//保存最终结果
    void backtracking(int n, int k, int beginIndex){
        //确定终止条件
        if(path.size() == k){
            //保存path到res
			res.push_back(path);
            return;//结束递归
        }

        //确定单层处理逻辑
        //遍历本层递归的数组，范围是[beginIndex, n]
        for(int i = beginIndex; i <= n; ++i){
            //添加当前路径节点值到path
            path.push_back(i);
            //进入下一层递归
            backtracking(n, k, i + 1);//跳过当前值
            //编写回溯处理逻辑
            //回溯时删掉当前层保存的值
            path.pop_back();
        }
    }
    vector<vector<int>> combine(int n, int k) {
		//可以先清一下两个结果数组
        //res.clear();
        //path.clear();
        backtracking(n, k, 1);//调用递归去操作数组
        return res;
    }
};

注意点

遍历本层递归时，i是要 小于等于 n的，并且beginIndex的初始值应该是1

这里需要厘清一个关系

本题中并不是真的有一个数组等着我们去遍历（分析时写[1,2,3,4]也只是便于理解），只是给定的一个范围，在该范围中找出所有两个元素的组合

因此要在[1,4]范围中找出所有两个元素的组合，就真的要从1开始，并且也要包含4

（不要错误的认为从1开始就漏了[1,2,3,4]中的1，结束位置是4就超出数组范围。因为根本就没有数组）

剪枝优化

TBD