P7448

problem & 双倍经验 & blog

低配版本

没有 Ynoi 标志性算法卡常，这点差评。

---

拆解问题

定义 \(lst_i\) 为上一个和 \(i\) 号点相同的位置。

由于几个转移都差不多，我们以 \([l,r - 1]\) 扩展到 \([l,r]\) 为例。

我们知道答案会加上 \([lst_r,r]\) 中 新出现的 且 \(> a_r\) 的数的 种类数。这个可以拆解为 \([l,r]\) 中大于 \(a_r\) 的种类数减 \([l,lst_r]\) 中 \(>a_r\) 的种类数。

经过转化，我们依然需要求 种类数。我们对于数组做一次扫描线，扫到 \(i\) 时，计算与 \(i\) 有关的贡献并且删除与 \(lst_i\) 有关的贡献。

所以问题就变成了求 总数。要求 单点加和区间内大于 \(x\) 的数的个数。那么这就是一个带权的二维数点。

因为我们使用了莫队二离，所以我们需要处理一下练个操作。

• \(O(n)\) 个修改即为加入 \(i\) 和删除 \(lst_i\)。

• \(O(n \sqrt m)\) 个询问。

注意在此处有两个性质：

• 第二维的值取决于第一维的值

• 保证所有的 \(x\) 坐标和 \(y\) 坐标不同

由于我们需要平衡复杂度，所以我们需要维护一个数据结构其修改操作的时间复杂度为 \(O(\sqrt n)\)，查询操作为 \(O(1)\)。

我们可以使用二维分块进行维护。

二维分块

注意：此处讲的与上面的有稍许不同，但本质一样。

假如说我们需要位于这样一个可爱的矩阵（左下角为 \([1,1]\)，右上角为需要询问的点）。

下面我们令 \(\mathbf{a} = n^{0.25},\mathbf{b} = n^{0.5},\mathbf{c} = n ^ {0.75}\)。

我们按照如下规则进行分块：

• 先分出 \(\sqrt n\) 个 \(\bf c \times c\) 个红块。

• 对于红块域分成 \(\sqrt n\) 个 \(\bf b \times b\) 个绿块。

• 接着将平面分成一个个大小为 \(n \times \mathbf{c}\) 个区域。然后分出 \(\sqrt n\) 个大小为 \(\bf c \times b\) 个橙块。

• 再竖着将平面分成一个个大小为 \(\mathbf{c} \times n\) 和区域，每个区域分成 \(\sqrt n\) 个大小为 \(\bf b \times c\) 个蓝块。

加入一个点时需要分别以红块，绿块，橙块和蓝块做二维前缀和。所以修改/加入的复杂度即为 \(O(\sqrt n)\)。

因此可以把一个询问分成这样。

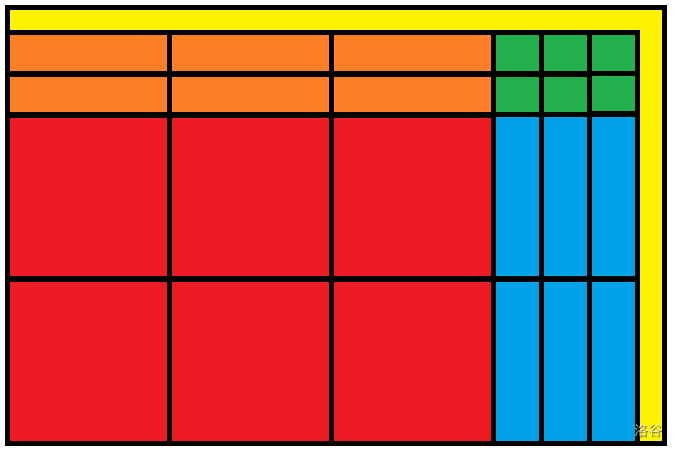
此处借了 \(\text{xfrvq}\) 大佬的图。

接下来就考虑散块的贡献，即为上图中黄色的区域。

由于上面的性质，我们可以把散块分成下面的样子：

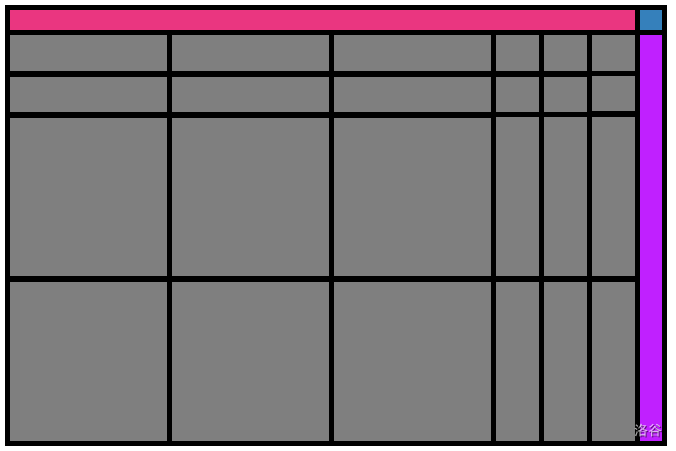
然后对于每一次的插入，我们枚举紫色范围内的 \(x\) 坐标，然后在查看 \(y\) 是否也在范围内，若是那就加上贡献。

对于粉色部分，我们枚举粉色范围内的 \(y\) 坐标，然后查看 \(x\) 坐标是否也在范围之内，若是则加上贡献。

然后注意蓝色区域块不要算重复就行了。

---

code