2021-02-23：给定一个正数n，求n的裂开方法数。规定：后面的数不能比前面的数小 。比如4的裂开方法有： 1+1+1+1、1+1+2、1+3、2+2、4，5种，所以返回5。

2021-02-23：给定一个正数n，求n的裂开方法数。规定：后面的数不能比前面的数小 。比如4的裂开方法有： 1+1+1+1、1+1+2、1+3、2+2、4，5种，所以返回5。

福哥答案2021-02-23：

自然智慧即可。

1.递归。有代码。

2.动态规划。dp是二维数组。有代码。

3.动态规划，空间压缩。两个一维数组搞定。有代码。

代码用golang编写，代码如下：

package main

import "fmt"

func main() {
    for i := 20; i < 40; i++ {
        fmt.Println(i, GetWays1(i), GetWays2(i), GetWays3(i))
    }
}

//1.递归
func GetWays1(n int) int {
    if n <= 0 {
        return 0
    }
    if n == 1 {
        return 1
    }
    return process1(1, n)
}
func process1(startMax int, rest int) int {
    if rest == 0 {
        return 1
    }
    ans := 0
    for i := startMax; i <= rest; i++ {
        ans += process1(i, rest-i)
    }
    return ans
}

//2.动态规划
func GetWays2(n int) int {
    if n <= 0 {
        return 0
    }
    if n == 1 {
        return 1
    }
    dp := make([][]int, n+1)
    for i := 0; i < n+1; i++ {
        dp[i] = make([]int, n+1)
    }
    for i := 1; i <= n; i++ {
        dp[i][0] = 1
        dp[i][i] = 1
    }

    for startMax := n - 1; startMax >= 1; startMax-- {
        for rest := startMax + 1; rest <= n; rest++ {
            dp[startMax][rest] = dp[startMax][rest-startMax] + dp[startMax+1][rest]
        }
    }

    return dp[1][n]

}

//3.动态规划，空间压缩
func GetWays3(n int) int {
    if n <= 0 {
        return 0
    }
    if n == 1 {
        return 1
    }
    dp := make([][]int, 2)
    for i := 0; i < 2; i++ {
        dp[i] = make([]int, n+1)
    }
    dp[1][0] = 1
    dp[1][n] = 1
    for startMax := n - 1; startMax >= 1; startMax-- {
        dp[0][startMax] = 1
        dp[0][0] = 1
        for rest := startMax + 1; rest <= n; rest++ {
            dp[0][rest] = dp[0][rest-startMax] + dp[1][rest]
        }
        dp[1], dp[0] = dp[0], dp[1]
    }
    return dp[1][n]

}

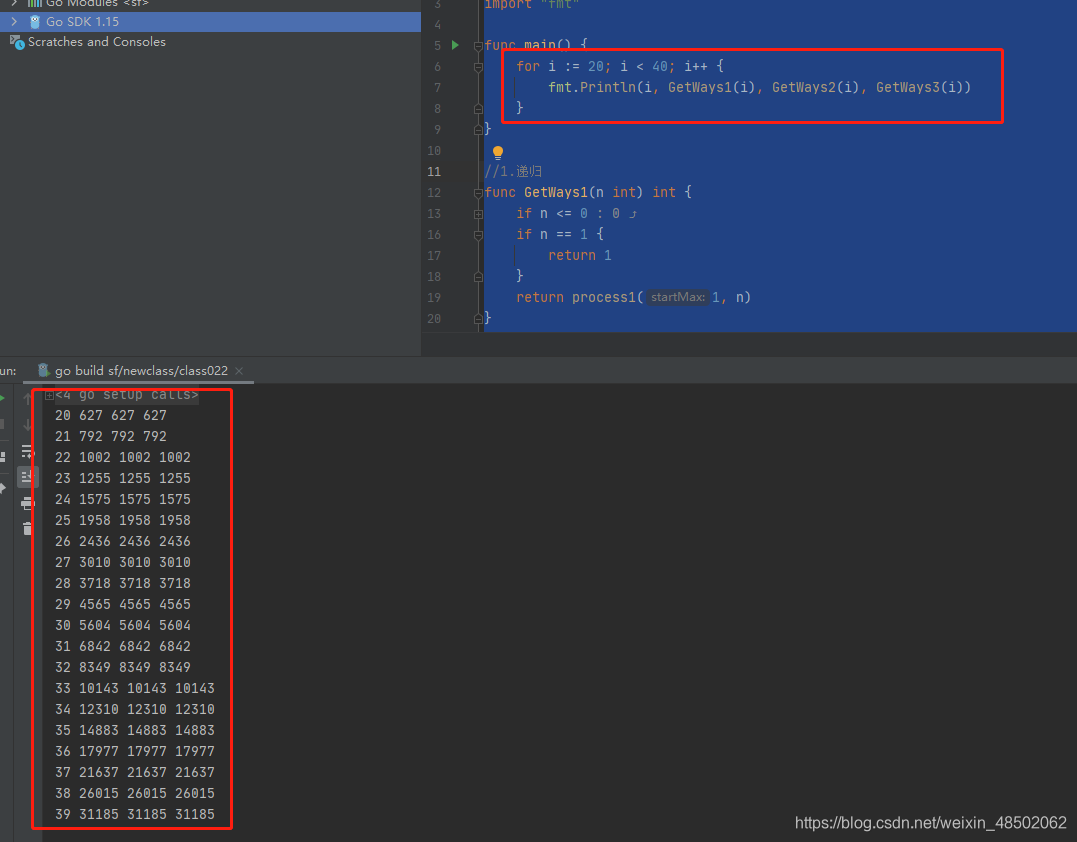
执行结果如下：

---

左神java代码

评论