算法设计和分析（Prim算法构建最小生成树）

问题：

给定无向图G（N，M）表明图G有N个顶点，M条边，通过Prim算法构造一个最小生成树

分析：

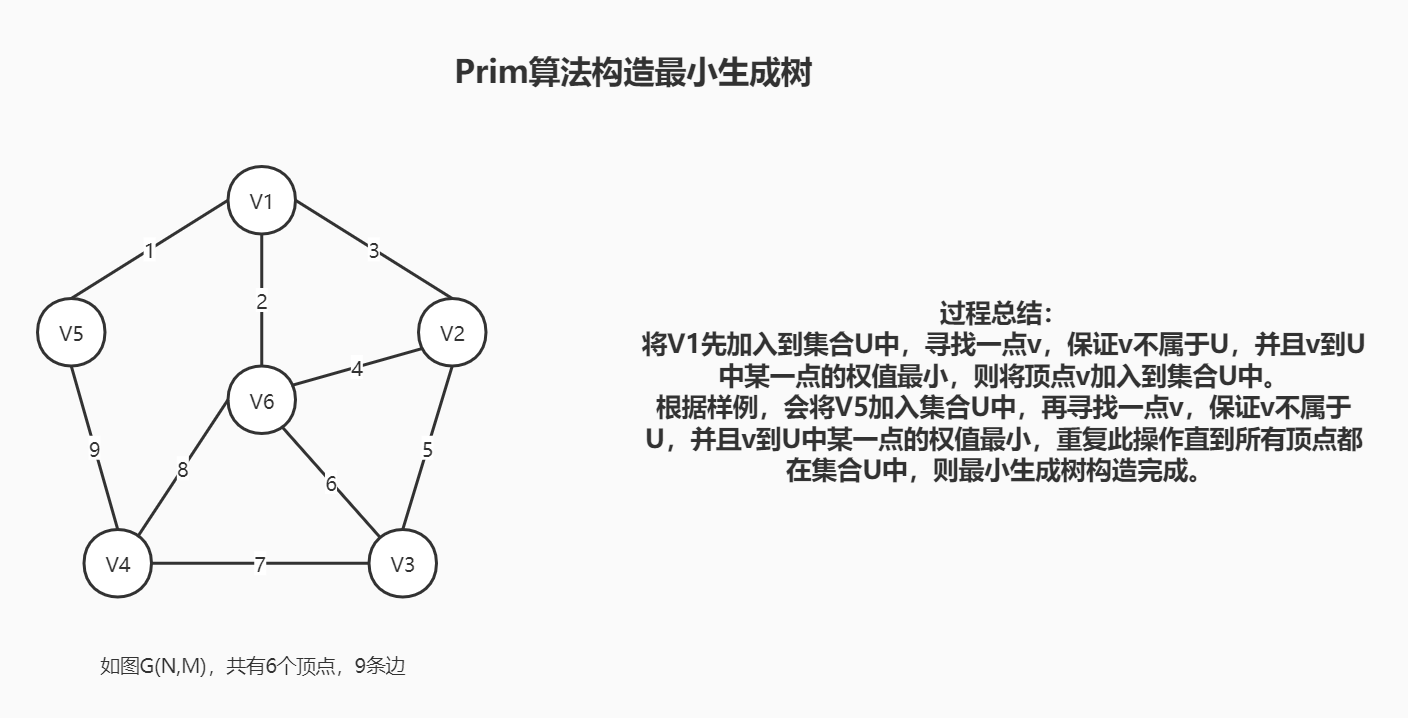
算法流程：

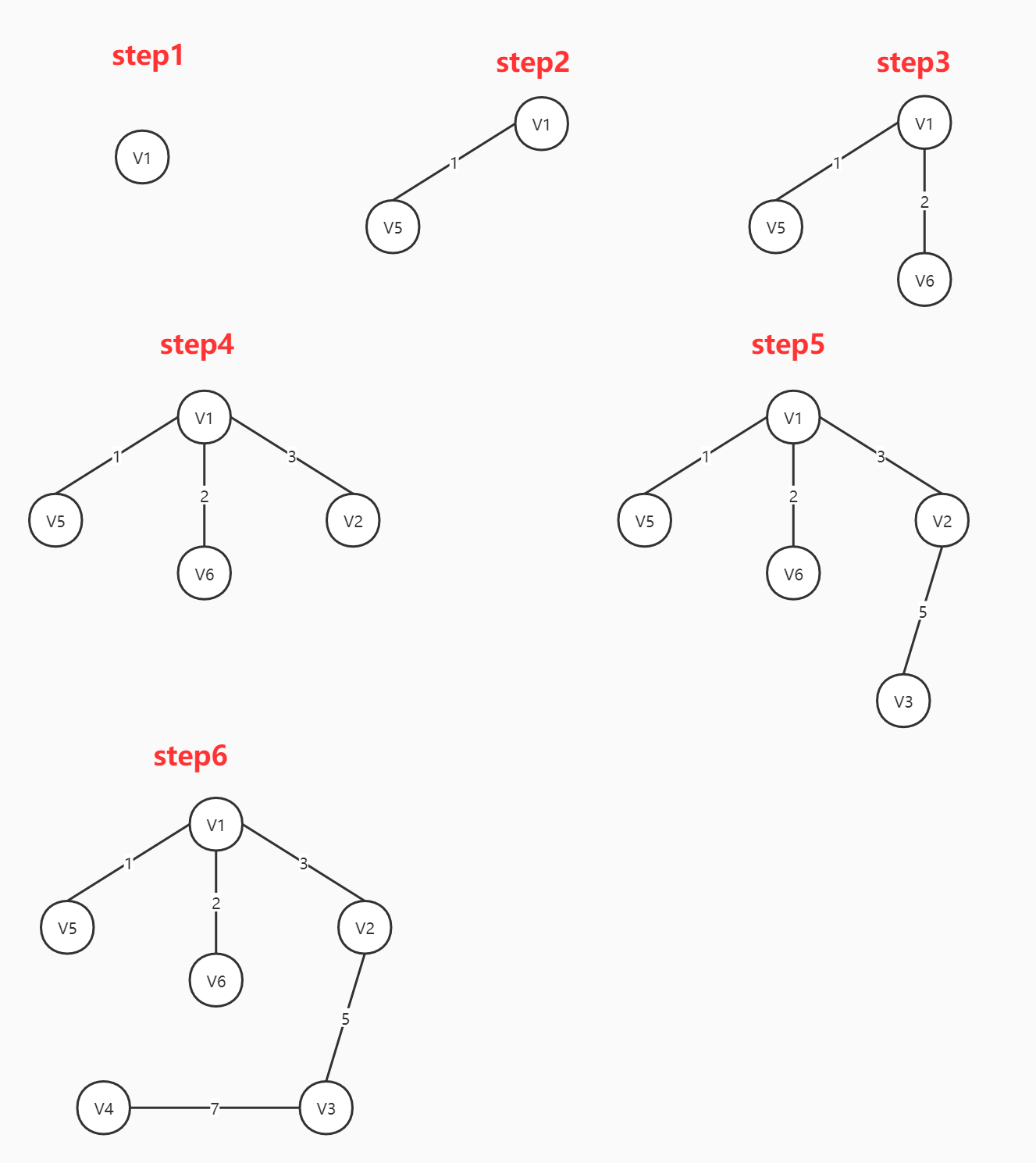
构造好的最小生成树就是step6

运行代码：

#include<cstdio>
#include<string.h>
#include<algorithm>
#include<cmath>
#include<iostream>
#include<vector>
#include<queue>
#include<set>
#include<map>
#include<cctype>
#include<stack>
#define ios ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define mem(a,x) memset(a,x,sizeof(a))
#define lson rt<<1,l,mid
#define rson rt<<1|1,mid + 1,r
#define P pair<int,int>
#define ull unsigned long long
using namespace std;
typedef long long ll;
const int maxn = ;
const ll mod = ;
const int inf = 0x3f3f3f3f;
const long long INF = 0x3f3f3f3f3f3f3f3f;
const double eps = 1e-;

int n, m;                                // 假设有n个点，m条边
int edge[maxn][maxn];                    // 用邻接矩阵来存图
int vis[maxn];                            // 记录某点是否加入最小生成树中
int dist[maxn];                            // 记录最小生成树中每一个点邻接的最短边
int father[maxn];                        // 记录某点的父亲节点，记录构成最小生成树的边
int main()
{

    scanf("%d %d", &n, &m);
    memset(edge, inf, sizeof edge);        // 将临界矩阵初始化为inf ,edge[u][v] == inf 代表u和v不连通
    for (int i = ; i <= n; ++i)        // 将数据进行初始化
    {
        vis[i] = false;
        father[i] = -;
        dist[i] = inf;
        edge[i][i] = ;
    }
    for (int i = ; i <= m; ++i)
    {
        int u, v,val;
        scanf("%d %d %d", &u, &v,&val);                // 获取边的起点、终点和权值
        edge[u][v] = min(val , edge[u][v]);
        edge[v][u] = min(val , edge[v][u]);            // 用邻接矩阵存图 ， 对于起点和终点相同的边仅保留最小值即可
    }
    vis[] = true;                                    // 将1号点添加进最小生成树中，作为树根
    for (int i = ; i <= n; ++i)
    {
        dist[i] = edge[][i];
        father[i] = ;
    }
    father[] = -;                                    // 将树根的父亲节点设为-1
    for (int i = ; i <= n; ++i)
    {
        int v = -;
        int tmp = inf;
        for (int j = ; j <= n; ++j)                // 在最小生成树之外寻找最短路径
        {
            if (!vis[j] && dist[j] < tmp)
            {
                v = j;
                tmp = dist[j];
            }
        }
        vis[v] = true;                                // 将寻找到的最短路径的终点加入最小生成树中
        for (int j = ; j <= n; ++j)
        {
            if (!vis[j] && edge[v][j] < dist[j])    // 在有新的点加入最小生成树之后，要更新dist中的值
            {
                dist[j] = edge[v][j];
                father[j] = v;
            }
        }
    }
    int sum = ;
    for (int i = ; i <= n; ++i) sum += dist[i];    //输出最小生成树的权值和，以及构成最小生成树的边
    printf("最小生成树的权值是：%d\n", sum);
    printf("构成最小生成树的边为：\n");
    for (int i = ; i <= n; ++i)
    {
        if (father[i] != -)
        {
            printf("%d %d\n", father[i], i);
        }
    }
    return ;
}

/*
6 9
1 5 1
1 6 2
1 2 3
2 6 4
2 3 5
3 6 6
3 4 7
4 6 8
4 5 9

样例

*/

Prim