signals function|KNN|SVM|average linkage|Complete linkage|single linkage
生物医疗大数据
存在系统误差使得估计量有偏,如下图红色和蓝色图形,存在随机误差使得估计量并不是同一个值,如图中除去期望之外的曲线值,为了控制随机抽样造成的误差,可以使用p-value决定是否服从假设检验,判断两个变量之间相关性的有无。
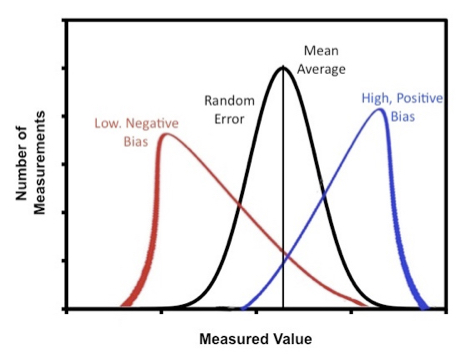
相关系数:该系数广泛用于度量两个变量之间的线性相关程度。
建立模型:
技术种类:线性模型&机器学习模型
按输出数据分类:监督学习模型&非监督学习模型
Average linkage demo

第一个矩阵是原始数据,单未知数据结构,通过average linkage方法结倒推得到其数据结构,即把数据展开了。主要步骤是找到Smallest distance(因为此两者之间的关系最简单),将距离均值作为到中间未知的距离(因为average linkage中的average决定的),随后以此类推。
除去average linkage方法之外还有Max:Complete linkage&min:single linkage。
对于classify来说,有data-base的KNN:K取值重要决定学习规则的范围;和Model-oriented其最重要的是找到区分多类数据的曲线,该曲线的函数思路可有以下三种:
1.高次项SVM(升维)
2.用傅里叶变换用三角函数凑不平滑曲线
3.signals function源自泰勒展开,通过将signals function加权得到划分曲线,这也是神经网络模型的基础
signals function|KNN|SVM|average linkage|Complete linkage|single linkage的更多相关文章
- 各常用分类算法的优缺点总结:DT/ANN/KNN/SVM/GA/Bayes/Adaboosting/Rocchio
1决策树(Decision Trees)的优缺点 决策树的优点: 一. 决策树易于理解和解释.人们在通过解释后都有能力去理解决策树所表达的意义. 二. 对于决策树,数据的准备往往是简单或者是不必要的. ...
- KNN算法的实现(R语言)
一 . K-近邻算法(KNN)概述 最简单最初级的分类器是将全部的训练数据所对应的类别都记录下来,当测试对象的属性和某个训练对象的属性完全匹配时,便可以对其进行分类.但是怎么可能所有测试对象都会找到 ...
- Adding New Functions to MySQL(User-Defined Function Interface UDF、Native Function)
catalog . How to Add New Functions to MySQL . Features of the User-Defined Function Interface . User ...
- 加载状态为complete时移除loading效果
一.JS代码: //获取浏览器页面可见高度和宽度 var _PageHeight = document.documentElement.clientHeight, _PageWidth = docum ...
- Stanford机器学习---第八讲. 支持向量机SVM
原文: http://blog.csdn.net/abcjennifer/article/details/7849812 本栏目(Machine learning)包括单参数的线性回归.多参数的线性回 ...
- Ajax之 beforeSend和complete longind制作
p.p1 { margin: 0.0px 0.0px 0.0px 0.0px; font: 15.0px Consolas; min-height: 18.0px } p.p2 { margin: 0 ...
- [RxJS] Observables can complete
The Observer object has the functions next() and error(). In this lesson we will see the other (and ...
- window.onload,<body onload="function()">, document.onreadystatechange, httpRequest.onreadystatechang
部分内容参考:http://www.aspbc.com/tech/showtech.asp?id=1256 在开发的过程中,经常使用window.onload和body onload两种,很少使用do ...
- KNN算法[分类算法]
kNN(k-近邻)分类算法的实现 (1) 简介: (2)算法描述: (3) <?php /* *KNN K-近邻方法(分类算法的实现) */ /* *把.txt中的内容读到数组中保存,$file ...
随机推荐
- Elasticsearch节点类型
当我们启动Elasticsearch的实例,就会启动至少一个节点.相同集群名的多个节点的连接就组成了一个集群. 在默认情况下,集群中的每个节点都可以处理http请求和集群节点间的数据传输,集群中所有的 ...
- php开启opcache
OPcache 通过将 PHP 脚本预编译的字节码存储到共享内存中来提升 PHP 的性能, 存储预编译字节码的好处就是 省去了每次加载和解析 PHP 脚本的开销. 一.php.ini配置opchche ...
- Julia1.x安装
删除julia-1.0 $ jupyter kernelspec list Available kernels: julia-1.0 /Users/keke.zhaokk/Library/Jupyte ...
- 你需要知道的 N 种抓取 dump 的工具
原总结注册表debug调试dump转储文件windbgprocdump 前言 今天,向大家介绍几种可以抓取应用程序转储文件的工具及基本使用方法.更详细的用法,请参考每个工具对应的帮助文档.如果你还不清 ...
- AQS: 什么是AQS?
AQS定义了一套多线程访问共享资源的同步器框架. 许多同步类实现都依赖于它,如常用的ReentrantLock/ReentrantReadWriterLock/CountDownLatch这些类里面都 ...
- 一、Cookie和Session介绍
会话跟踪 1. 什么是会话 * 用户拨打10086,从服务台接通后会话开始: * 用户发出话费查询请求,服务台响应.这是该会话中的一个请求: * 用户发出套餐变更请求,服务台响应.这是该会话中的 ...
- QLIKVIEW-SALESORDER\DELIVERYNOTICE\OUTSTOCK\INVOICE
//销售订单SALESORDER_TMP:NoConcatenateLOAD T_SAL_ORDER.LE_ID, [T_SAL_ORDER.LCY CODE], T_SAL_ORDER.SYSTEM ...
- 5)PHP,可变变量
所谓可变变量,就是一个变量的名,又是一个变量. 可变变量的语法是php的很特殊的语法——其他语言中少见. $v1 = “abc”; //这是一个字符串变量,其内容是字符串“abc” $abc = ; ...
- PAT甲级——1035 Password (20分)
To prepare for PAT, the judge sometimes has to generate random passwords for the users. The problem ...
- Linux 进程信号量
#include<stdlib.h> #include<stdio.h> #include<sys/types.h> #include<sys/ipc.h&g ...
