第7章 PCA与梯度上升法

主成分分析法：主要作用是降维

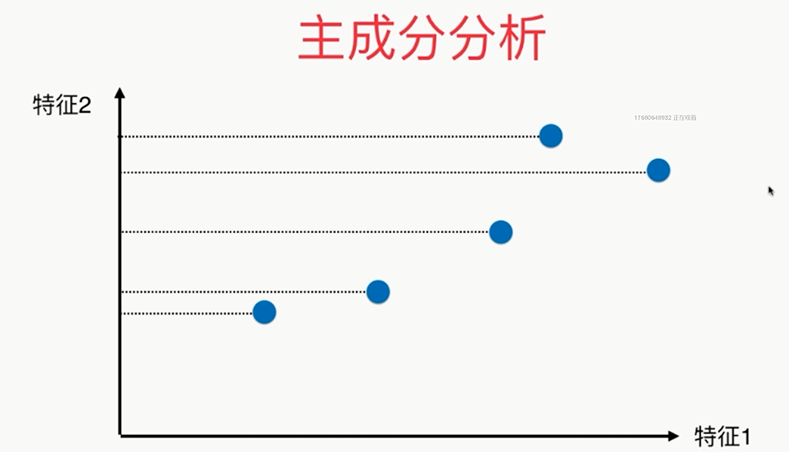
疑似右侧比较好？

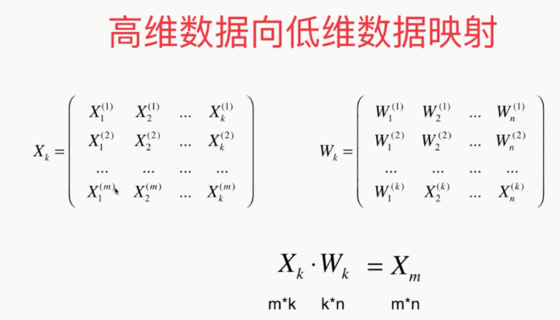
第三种降维方式：

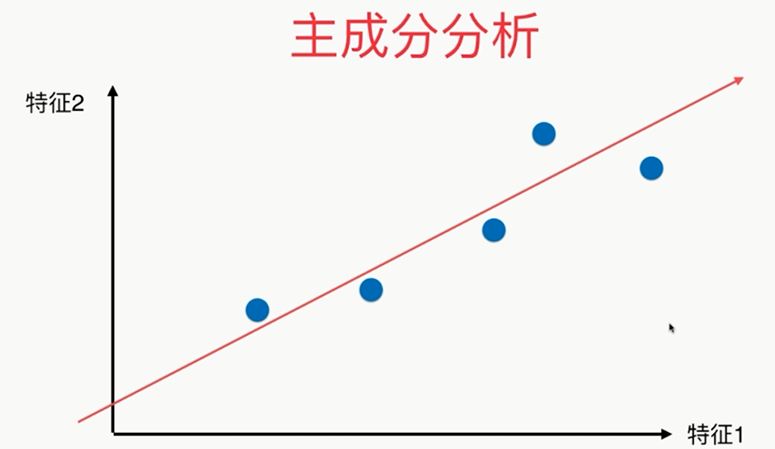
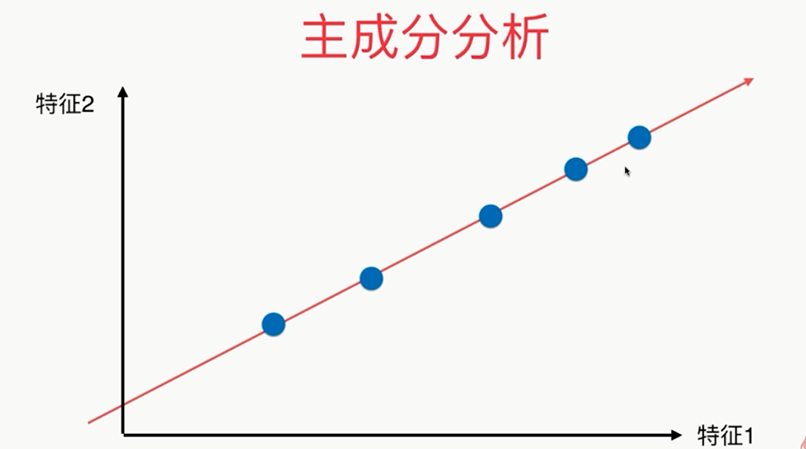
问题：？？？？？

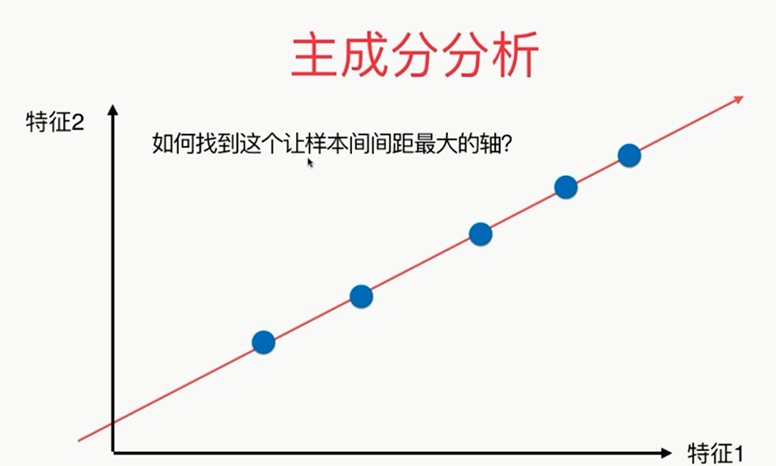
方差：描述样本整体分布的疏密的指标，方差越大，样本之间越稀疏；越小，越密集

第一步：

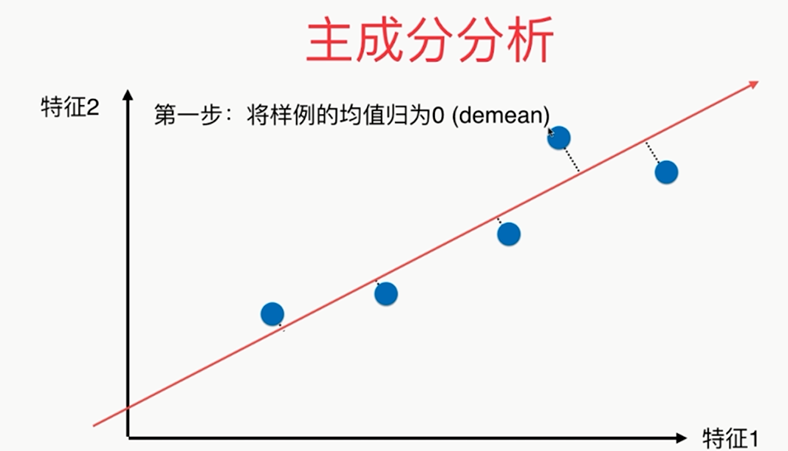
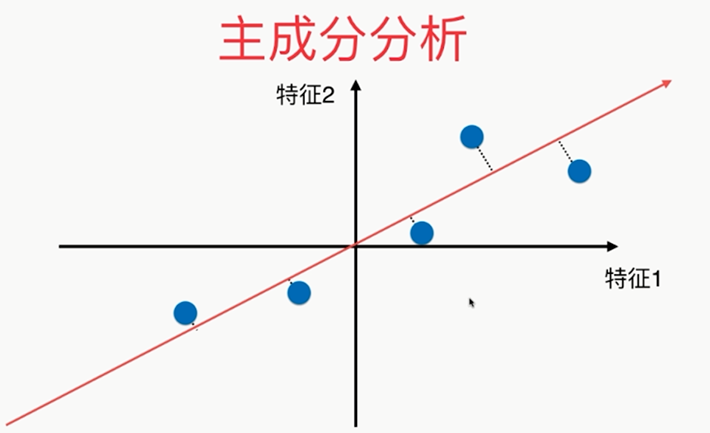
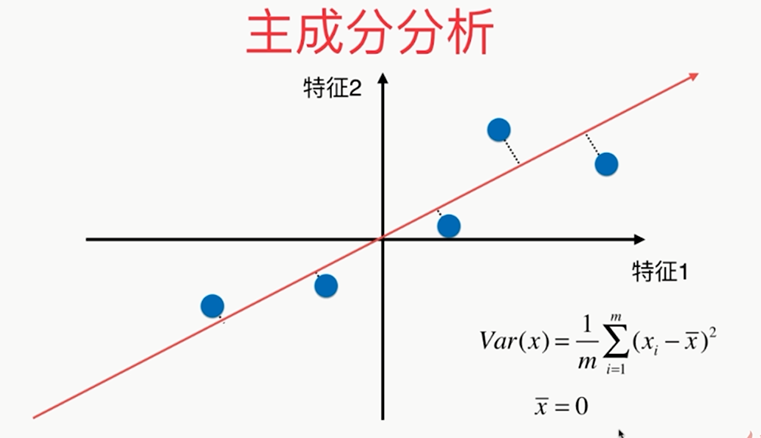
总结：

问题：？？？？怎样使其最大

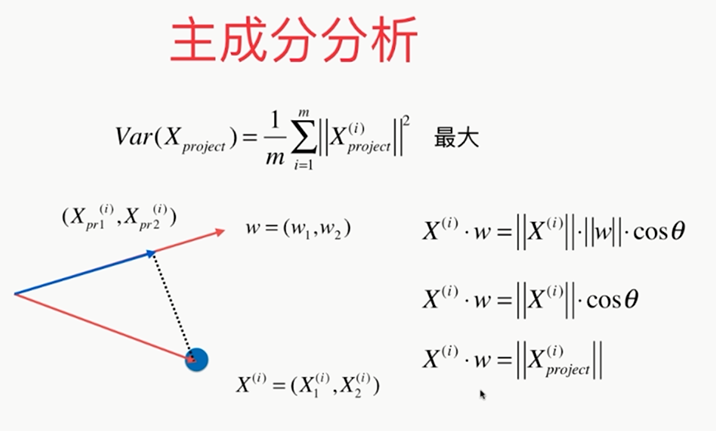
变换后：

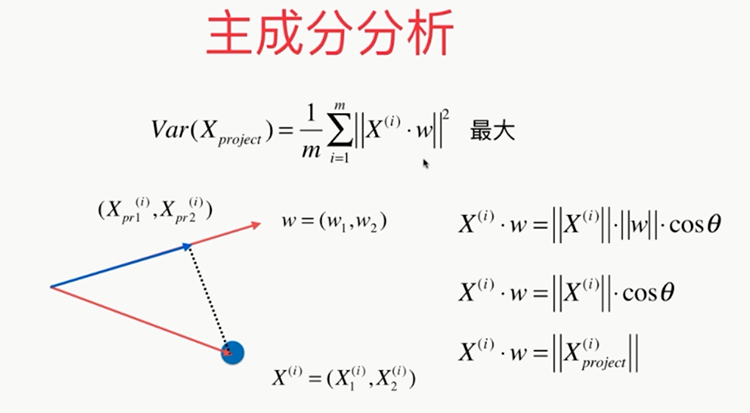
最后的问题：？？？？

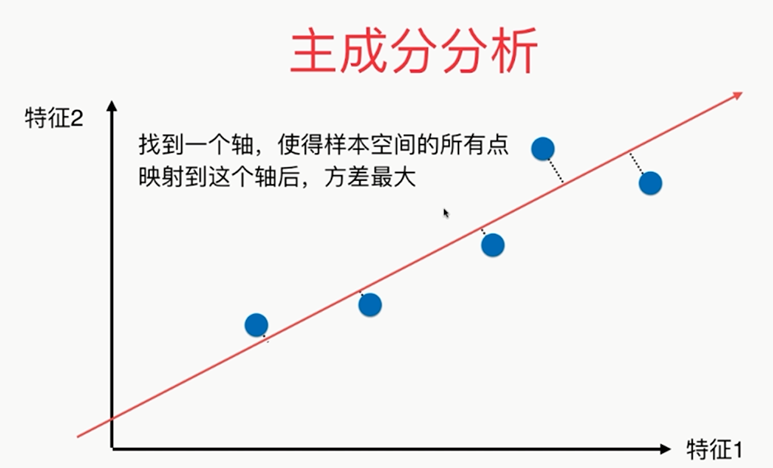
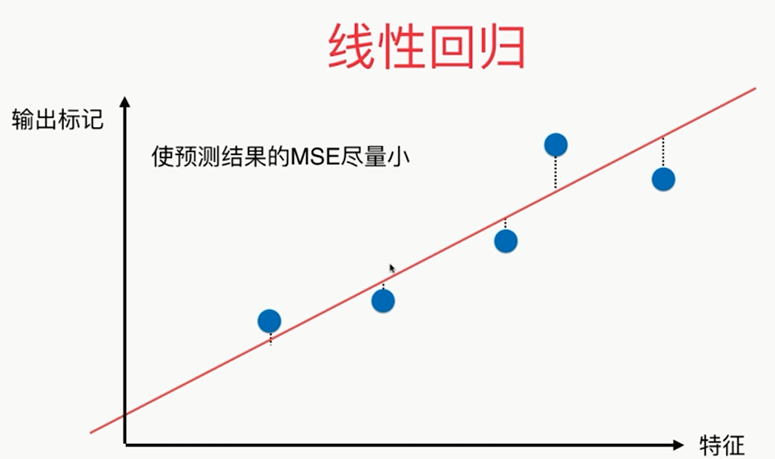
注意区别于线性回归

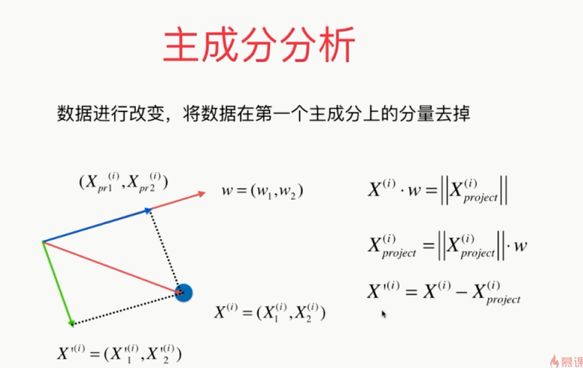
 使用梯度上升法解决PCA问题：

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
 
digits = datasets.load_digits()  # 手写识别数据
X = digits.data
y = digits.target
 
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)
# 使用K近邻
from sklearn.neighbors import KNeighborsClassifier
knn_clf=KNeighborsClassifier()
knn_clf.fit(X_train,y_train)
a1=knn_clf.score(X_test,y_test)
# print(a1)
# 使用PCA
from sklearn.decomposition import PCA
pca=PCA(n_components=2)
pca.fit(X_train)
X_train_reduction=pca.transform(X_train)
X_test_reduction=pca.transform(X_test)
knn_clf=KNeighborsClassifier()
knn_clf.fit(X_train_reduction,y_train)
a2=knn_clf.score(X_test_reduction,y_test)
# print(a2)
 
# print(pca.explained_variance_ratio_)
pca=PCA(n_components=X_train.shape[1])
pca.fit(X_train)
# print(pca.explained_variance_ratio_)
 
plt.plot([i for i in range(X_train.shape[1])],
        [np.sum(pca.explained_variance_ratio_[:i+1]) for i in range(X_train.shape[1])])
# plt.show()
 
pca1=PCA(0.95) # 能解释95%以上的方差
pca1.fit(X_train)
print(pca.n_components_)
 
from sklearn.decomposition import PCA
pca=PCA(0.95)
pca.fit(X_train)
X_train_reduction=pca.transform(X_train)
X_test_reduction=pca.transform(X_test)
knn_clf=KNeighborsClassifier()
knn_clf.fit(X_train_reduction,y_train)
a3=knn_clf.score(X_test_reduction,y_test)
print(a3)
 
pca=PCA(n_components=2)
pca.fit(X)
X_reduction=pca.transform(X)
for i in range(10):
    plt.scatter(X_reduction[y==i,0],X_reduction[y==i,1],alpha=0.8)
plt.show()

scikit-learn中的PCA