HDU-1828 Picture（扫描线 求矩形并的周长）

http://acm.hdu.edu.cn/showproblem.php?pid=1828

Time Limit: 6000/2000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)

Problem Description

A number of rectangular posters, photographs and other pictures of the same shape are pasted on a wall. Their sides are all vertical or horizontal. Each rectangle can be partially or totally covered by the others. The length of the boundary of the union of all rectangles is called the perimeter.

Write a program to calculate the perimeter. An example with 7 rectangles is shown in Figure 1.

The corresponding boundary is the whole set of line segments drawn in Figure 2.

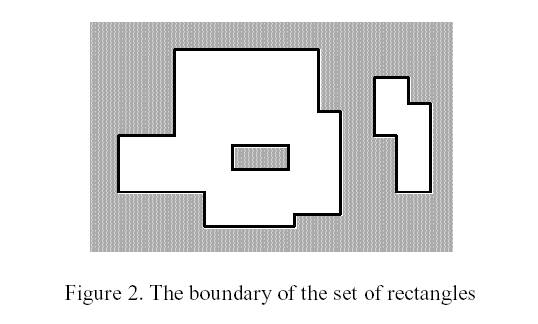
The vertices of all rectangles have integer coordinates.

Input

Your program is to read from standard input. The first line contains the number of rectangles pasted on the wall. In each of the subsequent lines, one can find the integer coordinates of the lower left vertex and the upper right vertex of each rectangle. The values of those coordinates are given as ordered pairs consisting of an x-coordinate followed by a y-coordinate. 
0 <= number of rectangles < 5000 
All coordinates are in the range [-10000,10000] and any existing rectangle has a positive area.
Please process to the end of file.

Output

Your program is to write to standard output. The output must contain a single line with a non-negative integer which corresponds to the perimeter for the input rectangles.

Sample Input

-
-
 -
 -  

Sample Output

题意：

有多个矩形，矩形的两边平行于坐标轴，这些矩形之间可能存在相互覆盖，求周长。

思路：

记录每个矩形的两条竖边（x1，y1，y2）和（x2，y1，y2），将所有的竖边按照x从小到大排序，然后一条一条竖边开始计算周长，那么以竖边所在的垂直于x轴的直线即是扫描线。

每次移动到一条新的竖边的时候，我们需要计算所在竖边扫描线上有用边长（即当前竖边的有用部分，可能当前的竖边被覆盖部分），以及加上当前扫描线与上一条扫描线之前的横边长 * 横边条数，

一直计算到最后一条竖边，即是完整周长了。

 

用一次扫描线，离散y坐标，按x从左到右扫描，统计每次总和的更改值，这样可以得到所有纵向边的和，对于横向边，可以用(Line[i].x - Line[i-1].x)*SegTree[1].num*2.前面的(Line[i].x - Line[i-1].x)相邻的两条线

段的x坐标的差，SegTree[1].num代表此时在线段树中一共有几条线段，每一条线段，就会增加这条线段的两个端点带来的横边。所以只要统计到当时有多少段覆盖的边，就可以得到那一段的横向的增加值

统计某一时刻有多少线段覆盖，可以用lf , rf记录这一个节点的两个端点是不是已经覆盖，如果覆盖值为1，那么这一段的num就是1，合并两个节点的时候，父节点的num等于左右子节点的num和，如果左节点

的rf与右节点的lf都是1，那么父节点的num值减去1。最后得到统计整个线段是由几个线段组成。

代码如下：

 #include <stdio.h>
 #include <string.h>
 #include <iostream>
 #include <string>
 #include <math.h>
 #include <algorithm>
 #include <vector>
 #include <queue>
 #include <set>
 #include <stack>
 #include <map>
 #include <math.h>
 const int INF=0x3f3f3f3f;
 typedef long long LL;
 const int mod=1e9+;
 const int maxn=1e5+;
 using namespace std;

 const int N=;
 struct Line_node
 {
     int x;//横坐标
     int y1,y2;//矩形纵向线段的左右端点
     int flag;//标记是入边还是出边
     bool operator < (const Line_node &s)
     {
         if(x==s.x)
             return flag>s.flag;
         else
             return x<s.x;
     }
 }Line[N*];

 struct SegTree_node
 {
     int l;
     int r;
     bool lf,rf;//左右边界点是否被覆盖;
     int cover_len;
     int cover_num;
     int num;//矩形数目
 }SegTree[maxn<<];

 vector<int> vt;

 void Build(int l,int r,int rt)
 {
     SegTree[rt].l=l;
     SegTree[rt].r=r;
     SegTree[rt].cover_len=;
     SegTree[rt].cover_num=;
     SegTree[rt].num=;
     SegTree[rt].lf=SegTree[rt].rf=false;
     if(l+==r)
         return ;
     int mid=(l+r)>>;
     Build(l,mid,rt<<);
     Build(mid,r,rt<<|);
 }

 void PushUp(int rt)
 {
     int l=SegTree[rt].l;
     int r=SegTree[rt].r;
     if(SegTree[rt].cover_num>)
     {
         SegTree[rt].cover_len=vt[r]-vt[l];
         SegTree[rt].lf=SegTree[rt].rf=true;
         SegTree[rt].num=;
         return ;
     }
 //    if(l+1==r)
 //    {
 //        SegTree[rt].cover_len=0;
 //        SegTree[rt].lf=SegTree[rt].rf=false;
 //        SegTree[rt].num=0;
 //        return ;
 //    }
     SegTree[rt].cover_len=SegTree[rt<<].cover_len+SegTree[rt<<|].cover_len;
     SegTree[rt].num=SegTree[rt<<].num+SegTree[rt<<|].num-(SegTree[rt<<].rf & SegTree[rt<<|].lf);//&按位与
     SegTree[rt].lf=SegTree[rt<<].lf;
     SegTree[rt].rf=SegTree[rt<<|].rf;
 }

 void Update(Line_node t,int rt)
 {
     int l=SegTree[rt].l;
     int r=SegTree[rt].r;
     if(t.y1<=vt[l]&&t.y2>=vt[r])
     {
         SegTree[rt].cover_num+=t.flag;
         PushUp(rt);
         return ;
     }
     int mid=(l+r)>>;
     if(t.y1<vt[mid])
         Update(t,rt<<);
     if(t.y2>vt[mid])
         Update(t,rt<<|);
     PushUp(rt);
 }

 int main()
 {
     int n;
     while (~scanf("%d",&n))
     {
         vt.clear();
         for(int i=;i<n;i++)
         {
             int x1,x2,y1,y2;
             scanf("%d %d %d %d",&x1,&y1,&x2,&y2);
             Line[i*].x=x1;
             Line[i*].y1=y1;
             Line[i*].y2=y2;
             Line[i*].flag=;

             Line[i*+].x=x2;
             Line[i*+].y1=y1;
             Line[i*+].y2=y2;
             Line[i*+].flag=-;
             vt.push_back(y1);
             vt.push_back(y2);
         }
         sort(Line,Line+*n);
         //y坐标离散化
         sort(vt.begin(),vt.end());
         int num=unique(vt.begin(),vt.end())-vt.begin();//去重并求出离散完的个数
         Build(,num-,);
         int ans=;//存累计面积
         int prelen=;//前一个L值,刚开始是0
         for(int i=;i<n*;i++)
         {
             if(i>)
             {//SegTree[1].num代表目前线分成了几段，每段两个点，每个点一条横变
                 ans+=SegTree[].num**(Line[i].x-Line[i-].x);//先加横边
             }
             Update(Line[i],);//更新线段树中维护的线
             ans+=abs(SegTree[].cover_len-prelen);//再加维护的线长度的变化值
             prelen=SegTree[].cover_len;
         }
         printf("%d\n",ans);
     }
     return ;
 }