平衡搜索树（二） Rb 红黑树

Rb树简介

红黑树是一棵二叉搜索树，它在每个节点上增加了一个存储位来表示节点的颜色，可以是Red或Black。通过对任何一条从根到叶子简单 路径上的颜色来约束，红黑树保证最长路径不超过最短路径的两倍，因而近似于平衡。（性质3、性质4保证了红黑树最长的路径不超过最短路径的两倍）

如图所示：

红黑树是满足下面红黑性质的二叉搜索树

1. 每个节点，不是红色就是黑色的

2. 根节点是黑色的

3. 如果一个节点是红色的，则它的两个子节点是黑色的

4. 对每个节点，从该节点到其所有后代叶节点的简单路径上，均包含相同数目的黑色节点。

好，现在了解了红黑树的特性之后，我们来开始创建红黑树。

//红黑树的节点的结构

 template<class K,class V>
 struct RedBlaceTreeNode
 {
     typedef RedBlaceTreeNode<K, V> Node;
     RedBlaceTreeNode(const K& key,const V& value)
         :_left(NULL), _right(NULL), _parent(NULL)
         , _key(key), _value(value), _col(RED)
     {}
 
     Node* _left;
     Node* _right;
     Node* _parent;
     K _key;
     V _value;
     Sign _col;
 };

//红黑树的结构

template<class K,class V>
class RedBlaceTree
{
    typedef RedBlaceTreeNode<K, V> Node;
public:
    RedBlaceTree()
        :_root(NULL)
    {}
public:
    bool _Push(const K& key, const V& value);
    void _LeftSpin(Node*& parent);
    void _RightSpin(Node*& parent);
    void _LeftRightSpin(Node*& parent);
    void _RightLeftSpin(Node*& parent);
 
    /*Check*/
    //1. 每个节点，不是红色就是黑色的
    //2. 根节点是黑色的
    //3. 如果一个节点是红色的，则它的两个子节点是黑色的
    //4. 对每个节点，从该节点到其所有后代叶节点的简单路径上，均包含相同数目的黑色节点
    void _Inorder(){ Inorder(_root); }
    void Inorder(Node* root);
protected:
    Node* _root;
};

//创建红黑树的函数 _Push()

插入的几种情况

cur为当前节点，p为父节点，g为祖父节点，u为叔叔节点

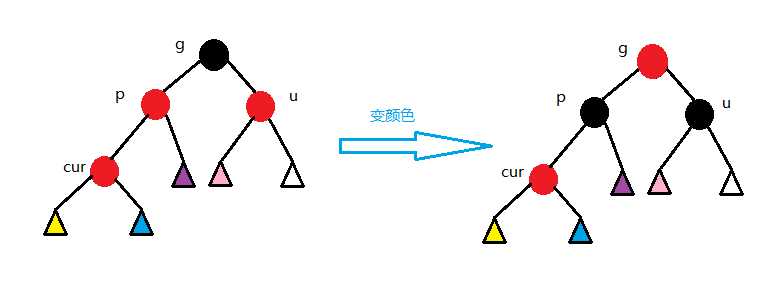
1.第一种情况 cur为红，p为红，g为黑，u存在且为红 则将p,u改为黑，g改为红，然后把g当成cur，继续向上调整。（ 还挺简单  O(∩_∩)O   继续往下看↓↓）

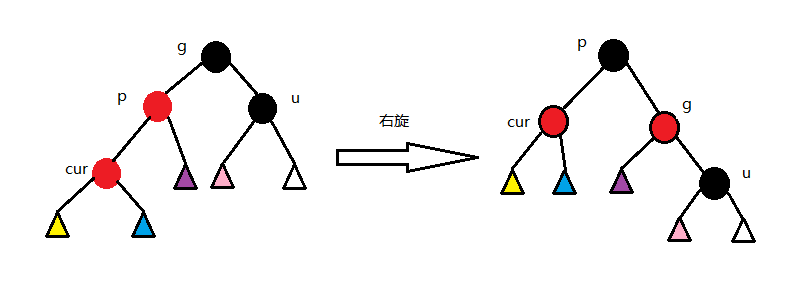
2.第二种情况 cur为红，p为红，g为黑，u不存在/u为黑 p为g的左孩子，cur为p的左孩子，则进行右单旋转；相反，p为g的右孩子，cur为p的右孩子，则进行左单旋转 p、g变色--p变黑，g变红

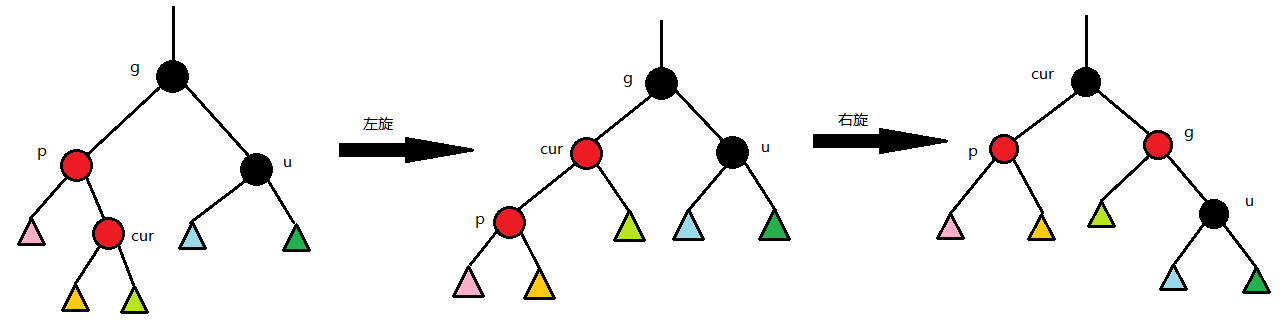
3.第三种情况 cur为红，p为红，g为黑，u不存在/u为黑
p为g的左孩子，cur为p的右孩子，则针对p做左单旋转；相反，p为g的右孩子，cur为p的左孩子，则针对p做右单旋转 则转换成了情况2

template<class K, class V>
bool RedBlaceTree<K, V>::_Push(const K& key, const V& value)
{
    Node* cur = _root;
    Node* parent = NULL;
    if (_root == NULL)
    {
        _root = new Node(key, value);
        _root->_col = BLACK;
    }
    else
    {
        while (cur)
        {
            parent = cur;
            if (key > cur->_key)
            {
                cur = cur->_right;
            }
            else if (key < cur->_key)
            {
                cur = cur->_left;
            }
            else
            {
                return false;
            }
        }
        cur = new Node(key, value);
        if (key > parent->_key)
        {
            parent->_right = cur;
            cur->_parent = parent;
        }
        else
        {
            parent->_left = cur;
            cur->_parent = parent;
        }
 
        if (parent->_col == RED)     //如果父亲节点为红色就需要调整
        {
            bool sign = false;      //标记位，用来标记grandparent是否为根节点
            while (cur->_parent)
            {
                Node* grandparent = NULL;
                Node* uncle = NULL;
                parent = cur->_parent;
                grandparent = parent->_parent;
 
                if (grandparent)       //如果祖父节点存在
                {
                    if (grandparent == _root)
                    {
                        sign = true;    //标记祖父节点是否为根节点
                    }
 
                    if (parent->_key > grandparent->_key)   //确定叔父节点
                    {
                        uncle = grandparent->_left;
                    }
                    else
                    {
                        uncle = grandparent->_right;
                    }
 
                    //第一种情况：cur为红，p为红，g为黑，u存在且为红
                    if (uncle && uncle->_col == RED)
                    {
                        parent->_col = BLACK;
                        uncle->_col = BLACK;
                        grandparent->_col = RED;
                        if (sign)
                        {
                            break;
                        }
                        cur = grandparent;
                    }
 
                    //第二种情况：cur为红，p为红，g为黑，u不存在/u为黑（单旋）
                    //第三种情况：cur为红，p为红，g为黑，u不存在/u为黑（双旋）
                    else
                    {
                        //第二
                        if (grandparent->_left == parent && parent->_left == cur)
                        {
                            grandparent->_col = RED;
                            parent->_col = BLACK;
                            _RightSpin(grandparent);
                            if (sign)
                            {
                                _root = grandparent;
                            }
                            break;
                        }
                        else if (grandparent->_right == parent && parent->_right == cur)
                        {
                            grandparent->_col = RED;
                            parent->_col = BLACK;
                            _LeftSpin(grandparent);
                            if (sign)
                            {
                                _root = grandparent;
                            }
                            break;
                        }
                        //第三
                        else if (grandparent->_left == parent && parent->_right == cur)
                        {
                            grandparent->_col = RED;
                            cur->_col = BLACK;
                            _LeftRightSpin(grandparent);
                            if (sign)
                            {
                                _root = grandparent;
                            }
                            break;
                        }
                        else if (grandparent->_right == parent && parent->_left == cur)
                        {
                            grandparent->_col = RED;
                            cur->_col = BLACK;
                            _RightLeftSpin(grandparent);
                            if (sign)
                            {
                                _root = grandparent;
                            }
                            break;
                        }
                    }
                }
                else   //cur 的上面只有一层
                {
                    break;
                }
            }
        }
    }
    _root->_col = BLACK;
}