Luogu3373【模板】线段树2

P3373【模板】线段树2

题目描述

如题，已知一个数列，你需要进行下面两种操作：

1.将某区间每一个数加上x

2.将某区间每一个数乘上x

3.求出某区间每一个数的和

输入输出格式

输入格式：

第一行包含三个整数N、M、P，分别表示该数列数字的个数、操作的总个数和模数。

第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。

接下来M行每行包含3或4个整数，表示一个操作，具体如下：

操作1：格式：1 x y k 含义：将区间[x,y]内每个数乘上k

操作2：格式：2 x y k 含义：将区间[x,y]内每个数加上k

操作3：格式：3 x y 含义：输出区间[x,y]内每个数的和对P取模所得的结果

输出格式：

输出包含若干行整数，即为所有操作3的结果。

输入输出样例

输入样例#1：

输出样例#1：

17
2

说明

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=8，M<=10

对于70%的数据：N<=1000，M<=10000

对于100%的数据：N<=100000，M<=100000

（数据已经过加强^_^）

样例说明：

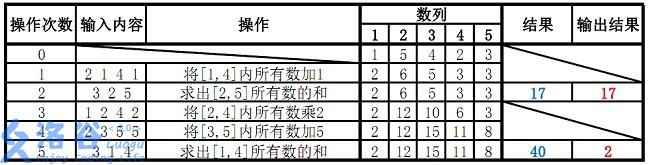
故输出应为17、2（40 mod 38=2）

线段树多个lazy标记的应用。

每个点上的标记表示自己儿子要乘或加上多少。

标记下放时，儿子节点的add标记与儿子节点的值分别先乘上父亲节点的乘标记再加上父亲节点的加标记（因为父亲节点的加标记已经乘上了一些乘标记了，不需要再乘一次）

儿子节点的乘标记直接乘上父亲节点的乘标记。

 #include<iostream>
 #include<cstdio>
 using namespace std;
 ;
 typedef long long ll;
 struct node{
     int l,r;
     ll val,add,time;
 }T[N*];
 ll Mod,a[N];
 inline void build(int l,int r,int x)
 {
     T[x].l=l;
     T[x].r=r;
     T[x].add=;
     T[x].time=;
     if(l!=r)
     {
         ;
         build(l,m,x*);
         build(m+,r,x*+);
         T[x].val=(T[x*].val+T[x*+].val)%Mod;
     }
     else T[x].val=a[l]%Mod;
 }
 inline ll cnt(int l,int r,int x)
 {
     if(l==T[x].l&&r==T[x].r) return T[x].val;
     ;i<=;i++)
     {
         T[x*+i].val=(T[x*+i].val*T[x].time+T[x].add*(T[x*+i].r-T[x*+i].l+))%Mod;
         T[x*+i].add=(T[x*+i].add*T[x].time+T[x].add)%Mod;
         T[x*+i].time=(T[x].time*T[x*+i].time)%Mod;
     }
     T[x].add=;
     T[x].time=;
     ll res=;
     ;
     );
     +);
     )+cnt(m+,r,x*+))%Mod;
     return res;
 }
 inline void addc(int l,int r,int x,ll c,int t)
 {
     if(l==T[x].l&&r==T[x].r)
     {
         )
         {
             T[x].time=(T[x].time*c)%Mod;
             T[x].val=(T[x].val*c)%Mod;
             T[x].add=(T[x].add*c)%Mod;
         }
         else
         {
             T[x].val=(T[x].val+c*(r-l+))%Mod;
             T[x].add=(T[x].add+c)%Mod;
         }
         return;
     }
     ;i<=;i++)
     {
         T[x*+i].val=(T[x*+i].val*T[x].time+T[x].add*(T[x*+i].r-T[x*+i].l+))%Mod;
         T[x*+i].add=(T[x*+i].add*T[x].time+T[x].add)%Mod;
         T[x*+i].time=(T[x].time*T[x*+i].time)%Mod;
     }
     T[x].add=;
     T[x].time=;
     ;
     ,c,t);
     +,c,t);
     else
     {
         addc(l,m,x*,c,t);
         addc(m+,r,x*+,c,t);
     }
     T[x].val=(T[x*].val+T[x*+].val)%Mod;
 }
 int main()
 {
     int n,m,t,l,r;
     ll k;
     scanf("%d%d%lld",&n,&m,&Mod);
     ;i<=n;i++) scanf("%lld",&a[i]);
     build(,n,);
     ;i<=m;i++)
     {
         scanf("%d%d%d",&t,&l,&r);
         ||t==)
         {
             scanf("%lld",&k);
             addc(l,r,,k,t);
         }
         ));
     }
     ;
 }