[Math Review] Statistics Basic: Estimation

Two Types of Estimation

One of the major applications of statistics is estimating population parameters from sample statistics. There are types of estimation:

• Point Estimate: the value of sample statistics

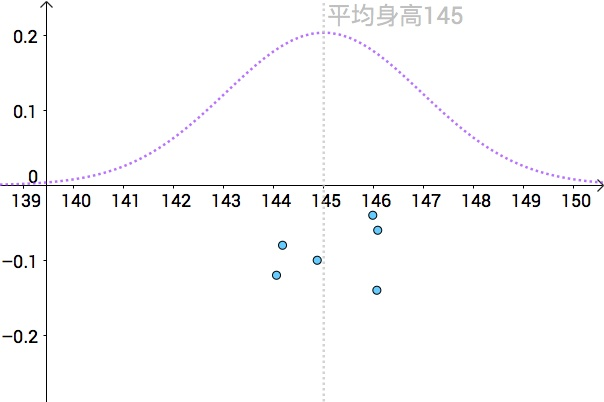
Point estimates of average height with multiple samples (Source: Zhihu)

• Confidence Intervals: intervals constructed using a method that contains the population parameter a specified proportion of the time.

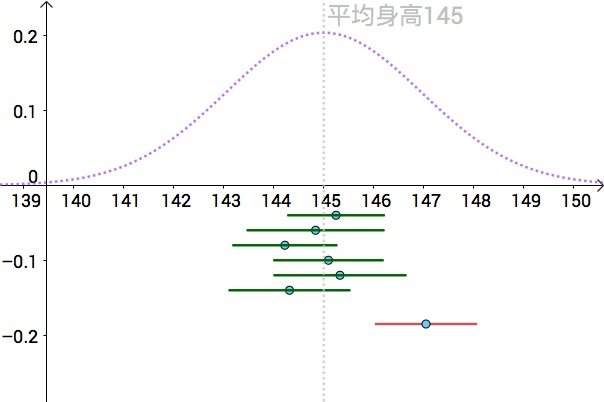
95% confidence interval of average height with multiple samples (Source: Zhihu)

Confidence Interval for the Mean

Population Variance is known

Suppose that M is the mean of N samples X₁, X₂, ......, X_n, i.e.

According to Central Limit Theorem, the the sampling distribution of the mean M is

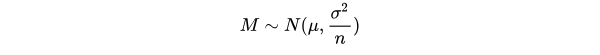
where μ and σ² are the mean and variance of the population respectively. If repeated samples were taken and the 95% confidence interval computed for each sample, 95% of the intervals would contain the population mean. So the 95% confidence interval for M is the inverval that is symetric about the point estimate μ so that the area under normal distribution is 0.95.

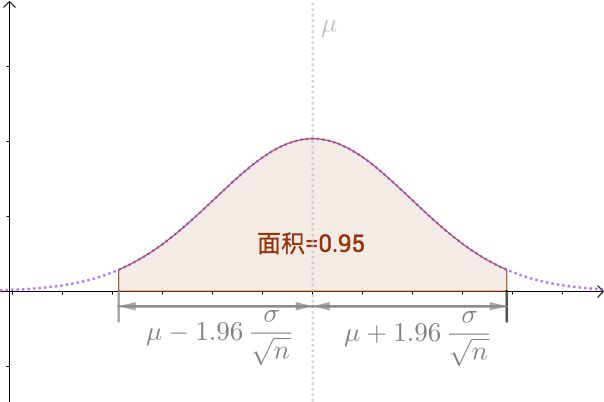
That is,

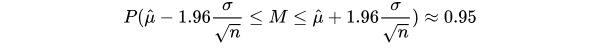
Since we don't know the mean of population, we could use the sample mean  instead.

Population Variance is Unknown

Dregree of Freedom

The degrees of freedom (df) of an estimate is the number of independent pieces of information on which the estimate is based. In general, the degrees of freedom for an estimate is equal to the number of values minus the number of parameters estimated en route to the estimate in question. 

If the variance in a sample is used to estimate the variance in a population, we couldn't calculate the sample variace as

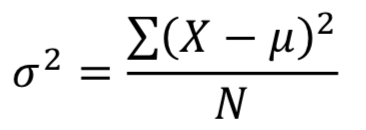
That's because we have two parameters to estimate (i.e., sample mean and sample variance). The degree of freedom should be N-1, so the previous formula underestimates the variance. Instead, we should use the following formula

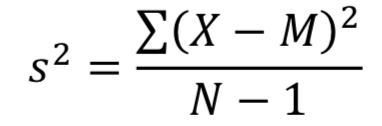
where s² is the estimate of the variance and M is the sample mean. The denominator of this formula is the degree of freedom.

Student's t-Distribution

Suppose that X is a random variable of normal distribution, i.e., X ~ N(μ, σ²)

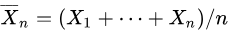
is sample mean and

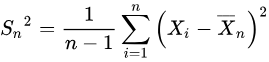
is sample deviation.

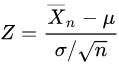
is a random variable of normal distribution.

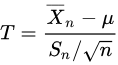
is a random variable of student's t distribution.

The probability density function of T is

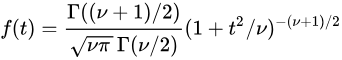
where  is the degree of freedom,  is a gamma function.

The t distribution is very similar to the normal distribution when the estimate of variance is based on many degrees of freedom, but has relatively more scores in its tails when there are fewer degrees of freedom. Here are t distributions with 2, 4, and 10 degrees of freedom and the standard normal distribution. Notice that the normal distribution has relatively more scores in the center of the distribution and the t distribution has relatively more in the tails.

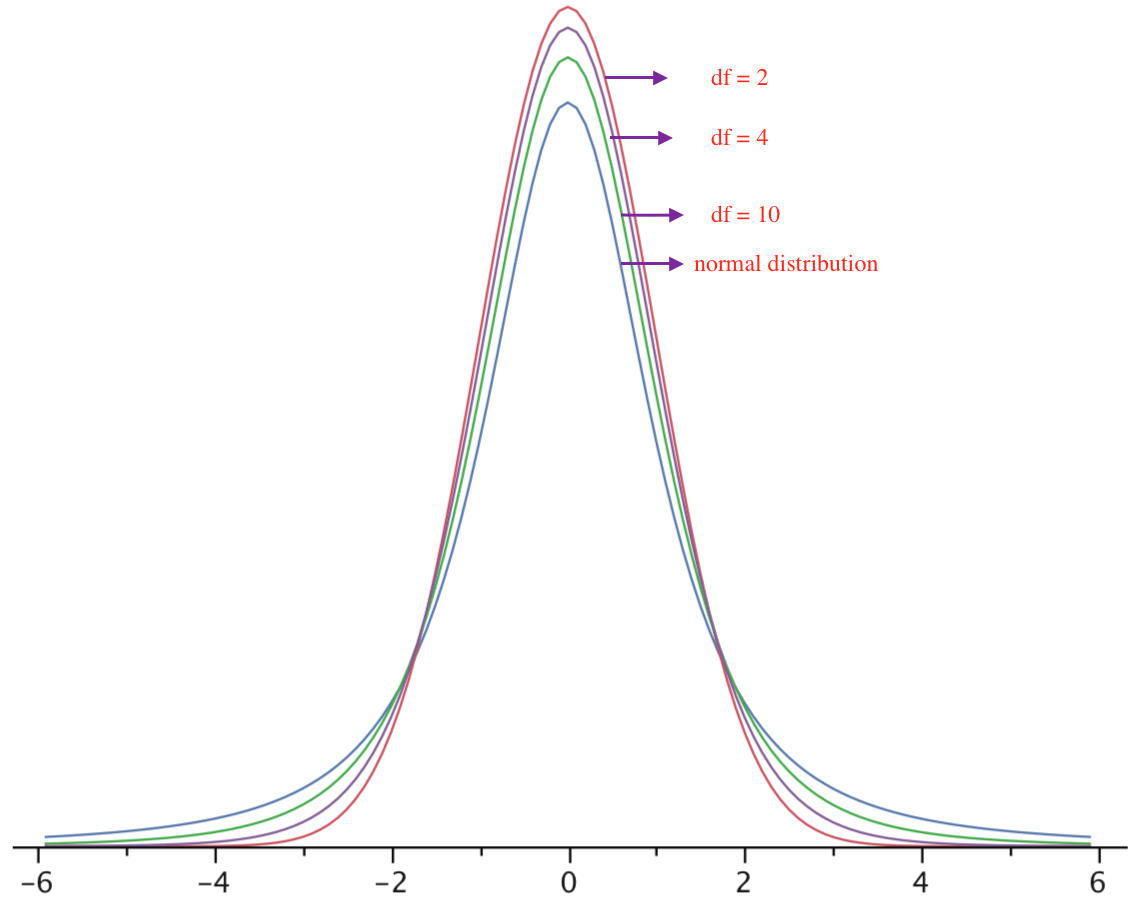
The t distribution is therefore leptokurtic. The t distribution approaches the normal distribution as the degrees of freedom increase. 

Confidence Interval of t Distribution

Now consider the case in which you have a normal distribution but you do not know the standard deviation. You sample N values and compute the sample mean (M) and estimate the standard error of the mean (σ_M) with s_M. What is the probability that M will be within 1.96 s_M of the population mean (μ)? This is a difficult problem because there are two ways in which M could be more than 1.96 s_M from μ: (1) M could, by chance, be either very high or very low and (2) s_M could, by chance, be very low. Intuitively, it makes sense that the probability of being within 1.96 standard errors of the mean should be smaller than in the case when the standard deviation is known (and cannot be underestimated).

Luckily, however, we can prove that random variable T will be student's t distribution. So we can use t distribution to estimate the mean of a normal distribution population in situations where the sample size is small and population standard deviation is unknown. For 90% confidence interval, it can be calculated as

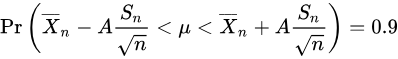
where A is value of T that contains 90% of the area of the t distribution for n-1 degree of freedom. We can calculate A through the t table.