Dijkstra 路径规划 C#

示例无向图如下：（起始点为v0）

邻接矩阵为：

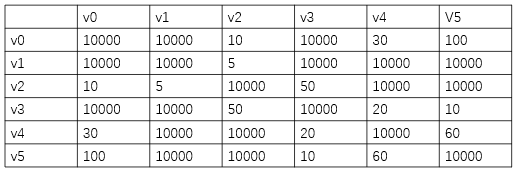
注意：其中没有连接的边和自己到自己的点权值用10000表示。

代码：

static void Main(string[] args)
{
　　int[,] graph = new int[,] { { , , , , ,  }, { , , , , ,  }, { , , , , ,  }, { , , , , ,  }, { , , , , ,  }, { , , , , ,  } };
　　int n = 6;
　　int[] S = new int[n]; //最短路径的顶点集合

　　string[] mid = new string[n];//点的路线
　　for (int i = ; i < n; i++)
　　{
　　　　S[i] = ;
　　　　mid[i] = "";
　　}
　　ShortestPathByDijkstra(n, graph, S, mid);
}

public static int IsContain(int m,int[] S)//判断该顶点是否已经计算过
{
　　int index = -;
　　for (int i = ; i < ; i++)
　　{
　　　　if (S[i] == m)
　　　　{
　　　　index = i;
　　　　}
　　}
　　return index;
}

/// <summary>
/// Dijkstrah实现最短路算法
/// </summary>
static void ShortestPathByDijkstra(int n,int[,] graph, int[] S, string[] mid)
{
　　int min;
　　int next;

　　for (int f = n-; f > ; f--)
　　{
　　　　//置为初始值
　　　　min = ;
　　　　next = ;//第一行最小的元素所在的列 next点
　　　　//找出第一行最小的列值
　　　　for (int j = ; j < n; j++)//循环第0行的列
　　　　{
　　　　　　if ((IsContain(j,S) == -) && (graph[, j] < min))//不在S中,找出第一行最小的元素所在的列
　　　　　　{
　　　　　　　　min = graph[, j];
　　　　　　　　next = j;
　　　　　　}
　　　　}
　　　　//将下一个点加入S
　　　　S[next] = next;
　　　　if (min == )
　　　　{
　　　　　　Console.WriteLine("V0到V{0}的最短路径为：无", next);
　　　　}
　　　　else
　　　　{
　　　　　　Console.WriteLine("V0到V{0}的最短路径为：{1},路径为：V0{2}->V{0}", next, min, mid[next]);
　　　　}
　　　　// 重新初始0行所有列值
　　　　for (int j = ; j < n; j++)//循环第0行的列
　　　　{
　　　　　　if (IsContain(j,S) == -)//初始化除包含在S中的
　　　　　　{
　　　　　　　　if ((graph[next, j] + min) < graph[, j])//如果小于原来的值就替换
          　　{
　　　　　　　　　　graph[, j] = graph[next, j] + min;
　　　　　　　　　　mid[j] = mid[next] + "->V" + next;//记录过程点
　　　　　　　　}
　　　　　　}
　　　　}
　　}
}

结果

　　

解析：

　　分三部分，主函数中给出图中的初始邻接矩阵，顶点个数。以及初始化最短路径的顶点集合和点路线集合。

　　IsContain(int m,int[] S)这个函数是在每次循环的时候判断该点是否已经在最短路径集合中，即已经遍历过。

　　接下来就是Dijkstra算法，大致步骤如下：

　　　　1、添加初始顶点v0在集合S中，遍历第一行，找最小的权值所在的顶点列值j。

　　　　2、将j值做为下一个点加入集合S中，输出此时到达j点的最小路径。

　　　　3、重新初始化第一行的值，通过判断加入某点后graph[next][j]+min是否小于graph[0, j]（其中j不在集合S中），若是则替换后者，并记录此过程 mid[j] = mid[next] + "->V" + next;

　　　　4、循环1、2、3步骤顶点数-1次。

　　

详细参考：https://blog.csdn.net/qq_25954259/article/details/78289335?locationNum=5&fps=1