P1168 中位数 堆

题目描述

给出一个长度为NN的非负整数序列A_iAi​，对于所有1 ≤ k ≤ (N + 1) / 21≤k≤(N+1)/2，输出A_1, A_3, …, A_{2k - 1}A1​,A3​,…,A2k−1​的中位数。即前1,3,5,…1,3,5,…个数的中位数。

输入格式

第11行为一个正整数NN，表示了序列长度。

第22行包含NN个非负整数A_i (A_i ≤ 10^9)Ai​(Ai​≤109)。

输出格式

共(N + 1) / 2(N+1)/2行，第ii行为A_1, A_3, …, A_{2k - 1}A1​,A3​,…,A2k−1​的中位数。

本题要用到优先队列定义堆：

such as：

　　　　priority_queue<int,vetor<int>,greater<int> >p1;——小根堆（扔进去的数据自动排为由小到大）

　　　　priority_queue<int,vector<int>,less<int> >p2; ——大根堆（扔进去的数据自动排为由大到小）

堆顶堆：

　　 

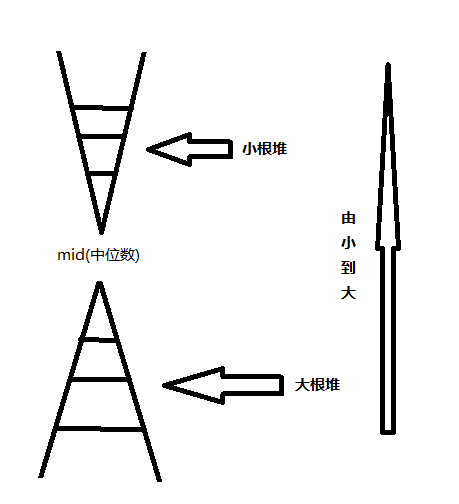
　代码（愿以后的我能看懂）：

 #include<bits/stdc++.h>
 using namespace std;
 priority_queue<int,vector<int>,less<int> >p2;
 priority_queue<int,vector<int>,greater<int> >p1;
 int n,x;
 int mid;
 int main()
 {
     cin>>n;
     cin>>x;
     mid=x;
     cout<<mid<<endl;//取中位数
     for(int i=;i<=n;i++)
     {
         cin>>x;
         if(x<mid)
             p2.push(x);
         if(x>mid)
             p1.push(x);
         if((i-)%==)
         {
             if(p1.size() >p2.size() )
             {
                 p2.push(mid);
                 mid=p1.top() ;
                 p1.pop() ;
             }
             if(p1.size() <p2.size() )
             {
                 p1.push(mid) ;
                 mid=p2.top() ;
                 p2.pop() ;
             }
             cout<<mid<<endl;
         }
     }
 return ;
 }