炸弹:线段树优化建边+tarjan缩点+建反边+跑拓扑

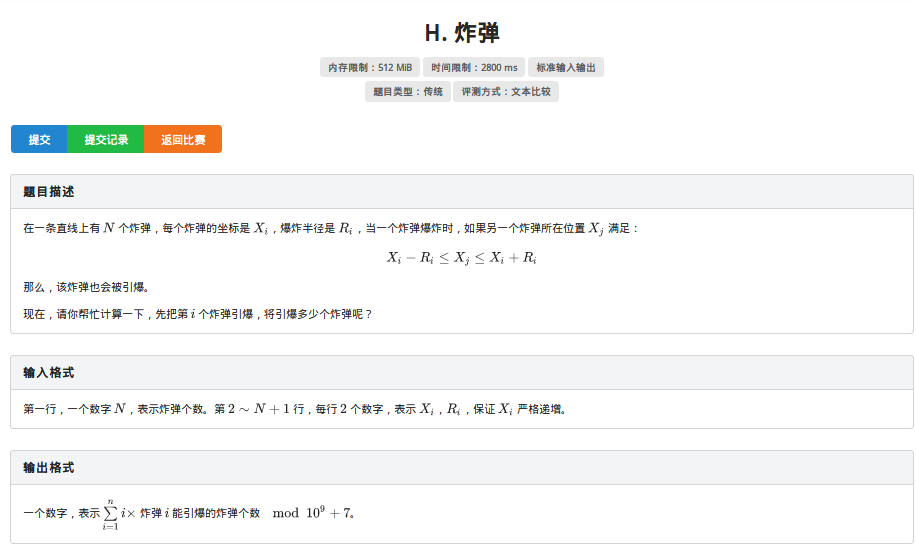
这道题我做了有半个月了...终于A了...

有图为证

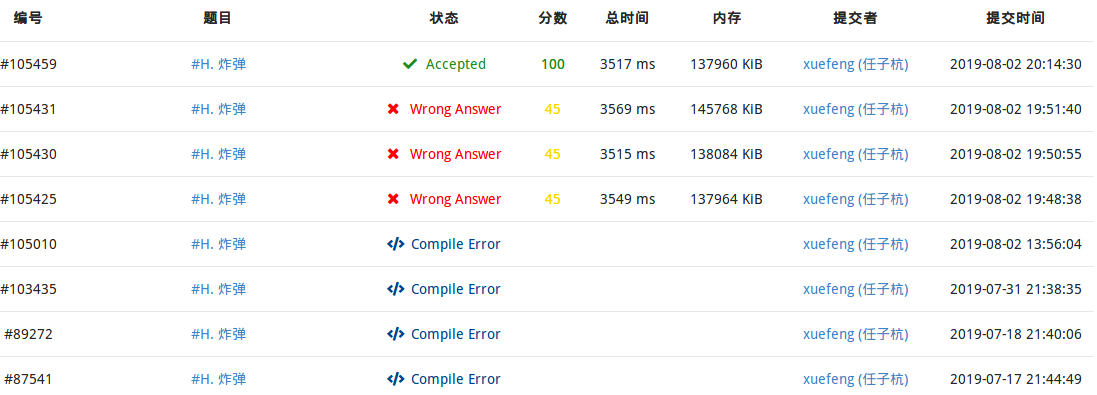
一句话题解:二分LR线段树优化建边+tarjan缩点+建反边+跑拓扑统计答案

首先我们根据题意,判断出来要炸弹可以连着炸,就是这个炸弹能炸到的可以是由它能炸到的其他炸弹来炸到.也就是说具有拓扑性.(a->b,b->c==a->c)

所以我们首先有了一个想法:建反图,tarjan缩点,跑拓扑.

为什么建反图?因为i能炸到j,所以j能炸到的i就可以炸到了,所以建反图从j->i可以实现这一点.

但是每个炸弹能炸到的是一个区间,怎么搞呢?

线段树优化建边,每次log次建边.

 //二分LR线段树优化建边+tarjan缩点+建反边+跑拓扑统计答案
 #include<bits/stdc++.h>
 #define N 500005
 #define INF 0x3f3f3f3f
 #define p 1000000007
 #define LL long long
 #define lch k<<1
 #define rch k<<1|1
 #define xx puts("xuefnngh");
 using namespace std;
 int n,num_bian,num_stack,num_dfn,num_tarjan;
 int ls[N<<],rs[N<<],tree[N],mx[N<<],mi[N<<],head[N<<],fm[N*],to[N*],nxt[N*];
 int dfn[N<<],low[N<<],sta[N<<],in_sta[N<<],Mi[N<<],Mx[N<<],bel[N<<],in_deg[N<<];
 LL dis[N],R[N];
 void add(int x,int y){if(x==y)return;/*printf("%d %d\n",x,y);*/to[++num_bian]=y;fm[num_bian]=x;nxt[num_bian]=head[x];head[x]=num_bian;}
 void Build(int k,int l,int r){
     ls[k]=l;rs[k]=r;mi[k]=INF;
     if(l==r)return (void) (tree[l]=k);
     Build(lch,l,(l+r)/);Build(rch,(l+r)/+,r);
     add(lch,k);add(rch,k);
 }
 void find(int k,int g,int L,int R){
     if(ls[k]==rs[k])return (void)(mx[k]=R,mi[k]=L);
     if(g<=rs[lch])find(lch,g,L,R);else find(rch,g,L,R);
     mx[k]=max(mx[lch],mx[rch]);mi[k]=min(mi[lch],mi[rch]);
 }
 void connect(int k,int l,int r,int g){
     if(ls[k]>=l&&rs[k]<=r) return (void) (add(k,g));
     if(l<=rs[lch])connect(lch,l,r,g);
     if(r>=ls[rch])connect(rch,l,r,g);
 }
 void tarjan(int x){
     dfn[x]=low[x]=++num_dfn;in_sta[x]=;sta[++num_stack]=x;
     for(int i=head[x];i;i=nxt[i])
         if(!dfn[to[i]])
             tarjan(to[i]),low[x]=min(low[x],low[to[i]]);
         else if(in_sta[to[i]])low[x]=min(low[x],dfn[to[i]]);
     if(dfn[x]==low[x]){
         int z;++num_tarjan;Mi[num_tarjan]=INF;
         /*printf("huan:%d\n",num_tarjan);*/
         do{
             z=sta[num_stack--];
             /*printf("%d ",z);*/
             bel[z]=num_tarjan;
             in_sta[z]=;
             Mi[num_tarjan]=min(Mi[num_tarjan],mi[z]);
             Mx[num_tarjan]=max(Mx[num_tarjan],mx[z]);
         }while(z!=x);
         /*puts("");
         printf("%d %d\n",Mi[num_tarjan],Mx[num_tarjan]);*/
     }
 }
 int que[N<<];
 void top_sort(){
     for(int i=;i<=num_tarjan;++i)if(!in_deg[i])que[++que[]]=i;
     for(int i=;i<=que[];++i)
         for(int j=head[que[i]];j;j=nxt[j]){
             --in_deg[to[j]];
             Mx[to[j]]=max(Mx[to[j]],Mx[que[i]]);Mi[to[j]]=min(Mi[to[j]],Mi[que[i]]);
             if(!in_deg[to[j]])que[++que[]]=to[j];
         }
 }
 int main(){
     scanf("%d",&n);Build(,,n);
     for(int i=;i<=n;++i)scanf("%lld%lld",&dis[i],&R[i]);
     for(int i=;i<=n;++i){
         int L=lower_bound(dis+,dis+n+,dis[i]-R[i])-dis;
         int RR=upper_bound(dis+,dis+n+,dis[i]+R[i])-dis-;
         /*printf("%d %d %d\n",i,L,RR);*/
         connect(,L,RR,tree[i]);find(,i,L,RR);/*printf("333%d\n",tree[i]);*/
     }
     for(int i=;i<=tree[n];++i)if(!dfn[i])tarjan(i);
     /*puts("xuueue");*/
     int num_pre=num_bian;num_bian=;memset(head,,sizeof head);
     for(int i=;i<=num_pre;++i)if(bel[fm[i]]!=bel[to[i]])add(bel[fm[i]],bel[to[i]]),in_deg[bel[to[i]]]++;
     top_sort();
     LL Ans=;for(int i=;i<=n;++i)(Ans+=(1ll*Mx[bel[tree[i]]]-Mi[bel[tree[i]]]+)*i%p+p)%=p/*,printf("%lld\n",Ans)*/;printf("%lld",Ans);
 }