[NOI1999]生日蛋糕（搜索）

[NOI1999]生日蛋糕

题目背景

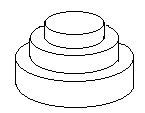
7月17日是Mr.W的生日，ACM-THU为此要制作一个体积为Nπ的M层

生日蛋糕，每层都是一个圆柱体。

设从下往上数第i(1<=i<=M)层蛋糕是半径为\(R_i\), 高度为\(H_i\)的圆柱。当i<M时，要求 \(R_i>R_{i+1}\) 且 \(H_i>H_{i+1}\) 。

由于要在蛋糕上抹奶油，为尽可能节约经费，我们希望蛋糕外表面（最下一层的下底面除外）的面积Q最小。

令Q= Sπ

请编程对给出的N和M，找出蛋糕的制作方案（适当的\(R_i\)和\(H_i\)的值），使S最小。

（除Q外，以上所有数据皆为正整数）

题目描述

输入输出格式

输入格式：

有两行，第一行为N（N<=20000），表示待制作的蛋糕的体积为Nπ；第二行为M(M<=15)，表示蛋糕的层数为M。

输出格式：

仅一行，是一个正整数S（若无解则S=0）。

输入输出样例

输入样例#1：

100

2

输出样例#1：

68

搜索的剪枝是真的恶心。

似乎我的代码还没有剪掉全部，太恶心没话说。

1.当前值不能更新答案，return。

2.当前值加上剩下体积能构成的最小表面积>ans，return。

3.枚举的蛋糕大小比剩余的体积大，break。

4.若选用当前蛋糕，剩余体积小于上方蛋糕的最小体积（预处理），break。

具体见代码

#include<bits/stdc++.h>
using namespace std;
int n,m,inf=2000000000,ans,sum,canvv[20010];
void dfs(int k,int lasth,int lastr,int canv)
{
    if(sum>=ans)return;if(sum+2*canv/lastr>ans)return;//1 2
    if(k==m+1)
    {
        if(canv)return;ans=min(ans,sum);return;
    }
    for(int h=m-k+1;h<min(canv+1,lasth);h++)
        for(int r=m-k+1;r<min(canv+1,lastr);r++)
        {
            if(h*r*r>canv)break;if(canv-h*r*r<canvv[k+1])break;//3 4
            if(k==1) sum+=r*r;
            sum+=2*r*h;
            dfs(k+1,h,r,canv-h*r*r);
            sum-=2*r*h;
            if(k==1) sum-=r*r;
        }
}
int main()
{
    scanf("%d%d",&n,&m);ans=inf;
    for(int i=m;i>=1;i--)
    canvv[i]=canvv[i+1]+(m-i+1)*(m-i+1)*(m-i+1);
    dfs(1,inf,inf,n);if(ans==inf)ans=0;cout<<ans<<endl;
}