sklearn 的 PolynomialFeatures 的用法

官方文档：http://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.PolynomialFeatures.html

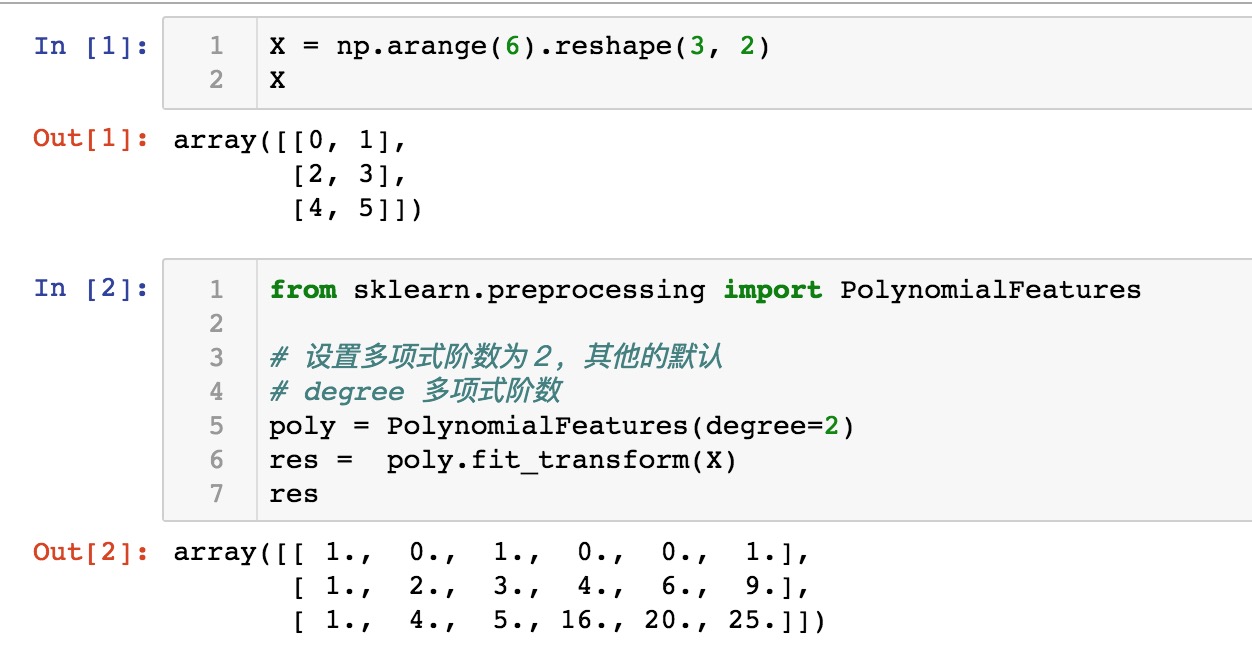
使用 sklearn.preprocessing.PolynomialFeatures 这个类可以进行特征的构造，构造的方式就是特征与特征相乘（自己与自己，自己与其他人），这种方式叫做使用多项式的方式。
例如：有 \(a\)、\(b\) 两个特征，那么它的 2 次多项式的次数为 \([1, a, b, a^2, ab, b^2]\)。

PolynomialFeatures 这个类有 3 个参数：

• degree：控制多项式的次数；
• interaction_only：默认为 False，如果指定为 True，那么就不会有特征自己和自己结合的项，组合的特征中没有 \(a^2\) 和 \(b^2\)；
• include_bias：默认为 True 。如果为 True 的话，那么结果中就会有 0 次幂项，即全为 1 这一列。

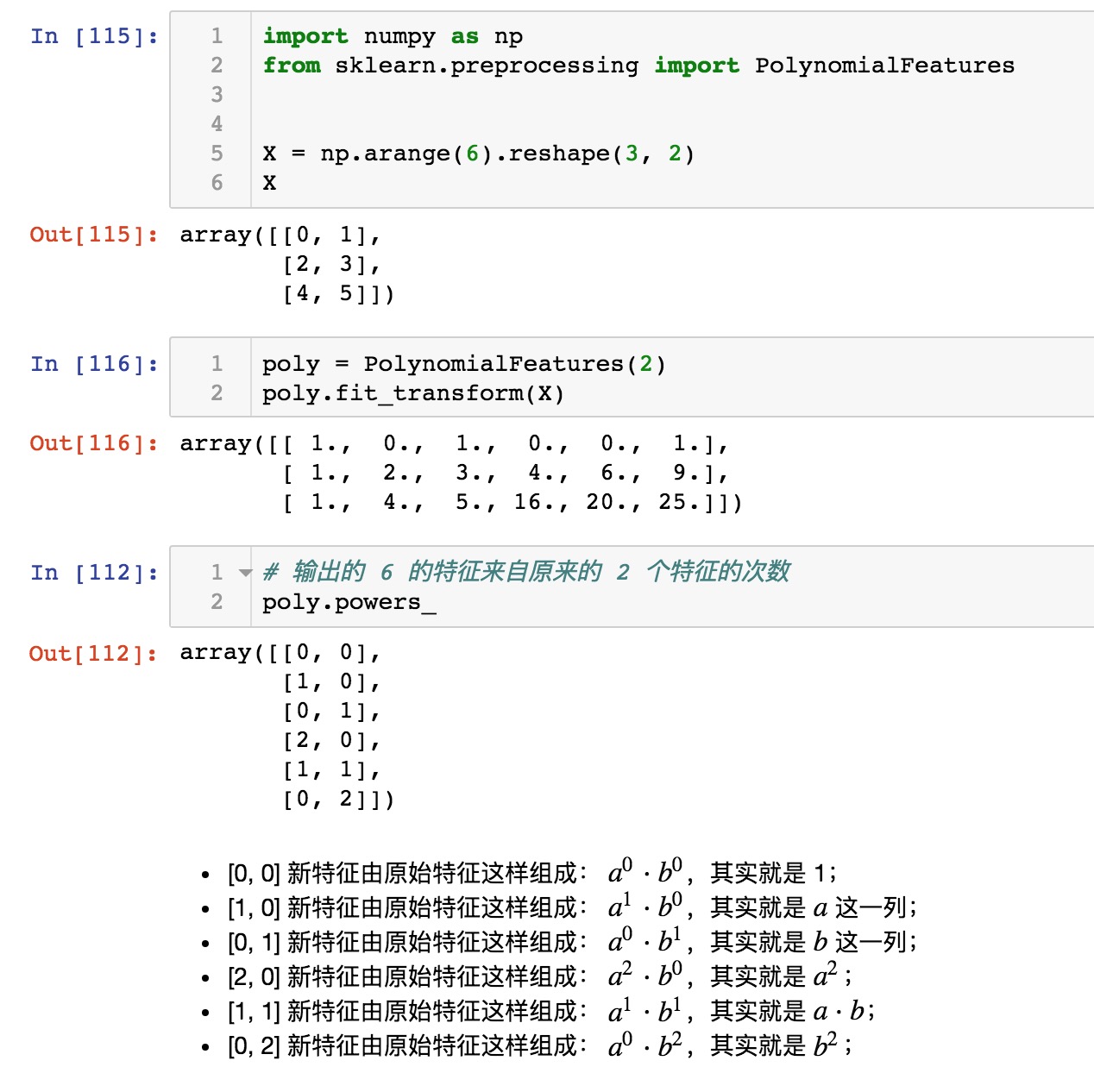
• interaction_only 的意思是，得到的组合特征只有相乘的项，没有平方项。
• interaction_only 设置成 True 的意思是： 例如 \([a, b]\) 的多项式交互式输出 \([1, a, b, ab]\)。
• include_bias 设置 0 次幂那一列是否要。