bzoj1367 可并堆

题面

参考：《左偏树的特点及运用——黄河源》

我们将这个数列划为很多个互不相交的区间，每一段区间内的 \(b\) 是相等的,即

• \(b[l[i]]=b[l[i]+1]=...=b[r[i]]=w[i]​\), \(l[i],r[i]​\) 为区间 \(i​\) 的左右端点

先假设题目时要求b不下降的(比较好讨论),那么答案应该会呈现出这样子：

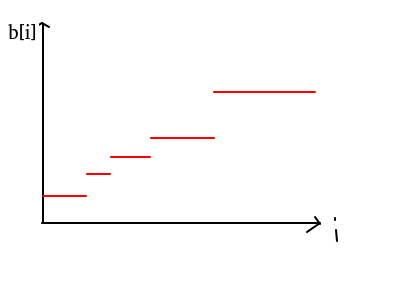
定理一：对于单个区间的最优解为其中位数，即 \(a[l[i]],a[l[i]+1],...,a[r[i]]\) 的最优解为 \(b[l[i]]=b[l[i]+1]=...=b[r[i]]=\) 中位数。

• 由绝对值的几何意义可得.

如果我们将"b不下降"这一条件忽略，单纯考虑单个区间的最优解，b可能是这样的：

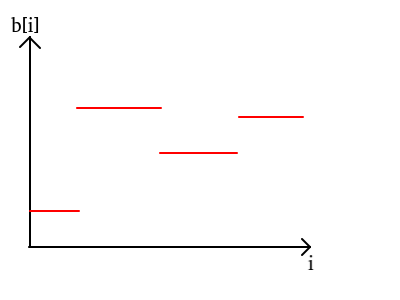
在讨论如何将不合法的最优解转化为合法的最优解之前，先来了解一些结论：

结论一：对于一段连续的a不下降(可能由多个区间组成)，则 \(b[i]=a[i]\) 时为最优解。

证明：该段绝对值之差为0.

引理一：对于相邻的两个区间 \([l[i]],\ r[i]]\ and\ [l[i+1],\ r[i+1]]​\) , \(u,v​\) 为其最优解，若 \(u\le v​\)， 则 \([l[i],r[i+1]]​\) 的区间最优解为 \(b[l[i]]=b[l[i]+1]=...=b[r[i]]=u,\ b[l[i+1]]=b[l[i+1]+1]=...=b[r[i+1]]=v​\).

证明：子问题最优 -> 整体最优.

引理二：对于相邻的两个区间 \([l[i]],\ r[i]]\ and\ [l[i+1],\ r[i+1]]\) , \(u,v\) 为其最优解，若 \(v < u\) ，则 \(b[r[i]]\le u, v\le b[l[i+1]].\)

画个图：

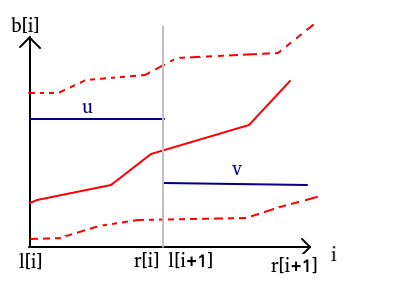
因为除此之外的情况(虚线)一定不会比这种情况更好

如：上面那条虚线没有u+右边部分更优，下面那条虚线没有v+左边部分更优

而u+右边部分与v+左边部分是属于红色折线的.

结论二：对于任意一个序列 \(a[1] , a[2] , ... , a[n]\) ,如果最优解为 \(( u , u , ... , u )\) , 那么在满足\(u ≤ u'\le b[1] \ or \ b[n] \le u' ≤ u\) 的情况下,\(( b[1] , b[2] , ... , b[n] )\) 不会比 \(( u′ , u′ , ... , u′ )\)更优。

给出 \(u\le u'\le b[1]\) 的证明，后者类似可证.

证明：

对于 \(n=1，a[1]=u,​\) 显然成立.

假设对于n是成立的，那么将 \(b[1],b[2]...b[n],b[n+1]\) 都设为 \(b[1]\) , 若解变得更坏了，则最优解应该是 \((u,u,...,u,b[n+1])\) 而不是 \((u,u,...u,u)\), 而由几何意义得 \((b[1],b[1]...b[1])\) 比 \((u',u',...,u')\) 会差，故对于 \(n+1\) 也成立.

由数学归纳原理可得命题成立.

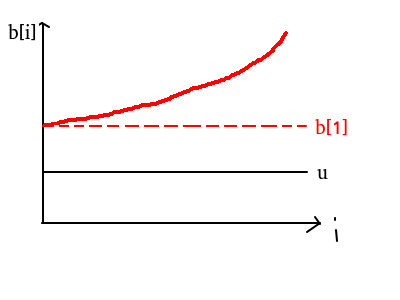
至此，我们已经可以将局部最优解合成整体最优解了!

一：

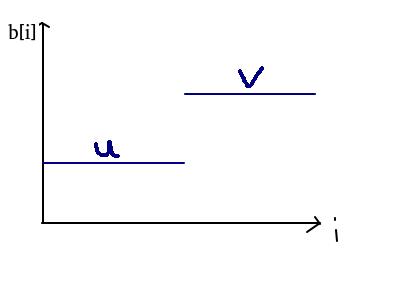
u，v为两段区间的最优解，由引理一全局最优解为 \((u,u,...,u,v,v,...,v)\).

二：

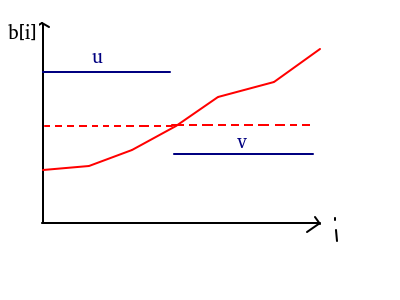
这种情况较为复杂，由引理二可得最优解一定是左边\(\le u\), 右边的 \(\geq v\)，即为红色部分，

又由结论二得虚线部分比红色部分更优(其实是不会更差), 所以这个整个区间的最优解一定为一个定值!

注：其实左边的虚线是比右边低的，但是左边的虚线越往上越优，右边的虚线越往下越优，故最优时它们高度相同，为一定值。

接下来就转换成求这个定值了。

由定理一，值该定值即为整个数列的中位数!!

所以一开始假设每个数就是一个区间，然后不断合并区间，最终知道全局最优解。

• 假设我们已经找到前 \(k\) 个数 \(a[1], a[2], ... , a[k] (k<n)\) 的最优解,
• 得到 \(m\) 个区间组成的队列, 对应的解为 \((w[1], w[2] , ... , w[m])\),
• 现在要加入 \(a[k+1]\), 并求出前 \(k+1\) 个数的最优解。
• 首先我们把 \(a[k+1]\) 作为一个新区间直接加入队尾,令 \(w[m+1]=a[k+1]\) ,
• 然后不断检查队尾两个区间的解 \(w[m]\) 和 \(w[m+1]\),如果 ​\(w[m] > w[m+1]\) ,
• 我们需要将最后两个区间合并,并找出新区间的最优解(也就是序列 \(a​\) 中,下标在这个新区间内的各项的中位数)。
• 重复这个合并过程,直至 \(w[1] ≤ w[2] ≤ ... ≤ w[m]​\) 时结束,然后继续处理下一个数。
• 画图理解...

现在我们需要考虑一下数据结构的选取,

算法中涉及到以下两种操作:

1.合并两个有序集

2.查询某个有序集内的中位数

我们很容易想到平衡树，但是就算是启发式合并，复杂度也有 \(O(nlog^2n)​\), \(1e6​\) 过不了.

我们可以用大根堆来维护每个区间内的中位数，我们发现右端的堆都是单个元素的加入，只要一下降，就会合并，所以合并是正确的。

“通过进一步分析,我们发现,只有当某一区间内的中位数比后一区间内的中位数大时,合并操作才会发生,也就是说,任一区间与后面的区间合并后,该区间内的中位数不会变大。于是我们可以用最大堆来维护每个区间内的中位数,当堆中的元素大于该区间内元素的一半时,删除堆顶元素,这样堆中的元素始终为区间内较小的一半元素,堆顶元素即为该区间内的中位数。” —— 黄源河

堆顶元素即为该区间内的中位数。

考虑到我们必须高效地完成合并操作,左偏树是一个理想的选择,每个操作都是 \(O(logn)\),

总时间复杂度 \(O(nlogn)​\).

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;

int read() {
    register int x = 0, f = 1; register char c;
    while (!isdigit(c = getchar())) if (c == '-') f = -1;
    while (x = (x << 1) + (x << 3) + (c ^ 48), isdigit(c = getchar()));
    return x * f;
}

const int N = 1e6 + 3;
int n, l[N], r[N], tot[N], b[N], size[N], dis[N] = {-1}, val[N], root[N], ch[N][2], w[N];
int merge(int x, int y) {
    if (!x) return y;
    if (!y) return x;
    if (val[x] < val[y]) swap(x, y);
    ch[x][1] = merge(ch[x][1], y);
    size[x] = size[ch[x][0]] + size[ch[x][1]] + 1;
    if (dis[ch[x][0]] < dis[ch[x][1]]) swap(ch[x][1], ch[x][0]);
    dis[x] = dis[ch[x][1]] + 1;
    return x;
}
int main() {
    freopen("xhc.in", "r", stdin);
    freopen("xhc.out", "w", stdout);

    n = read();
    for (int i = 1; i <= n; ++ i) val[i] = read(), val[i] -= i;

    int now = 0;
    for (int i = 1; i <= n; ++ i) {
        now ++;
        l[now] = r[now] = i;
        root[now] = i;
        tot[now] = size[root[now]] = 1;
        while (now > 1 and val[root[now - 1]] > val[root[now]]) {
            now --;
            r[now] = r[now + 1], tot[now] += tot[now + 1];
            root[now] = merge(root[now], root[now + 1]);
            while (size[root[now]] * 2 > (tot[now] + 1)) {
                root[now] = merge(ch[root[now]][0], ch[root[now]][1]);
            }
        }
    }
    long long ans = 0;
    for (int i = 1; i <= now; ++ i) {
        for (int j = l[i]; j <= r[i]; ++ j) {
            ans += 1ll * (val[root[i]] - val[j] < 0 ? val[j] - val[root[i]] : val[root[i]] - val[j]);
        }
    }
    printf("%lld\n", ans);
   /* for (int i = 1; i <= now; ++ i) {
        for (int j = l[i]; j <= r[i]; ++ j) {
            cout << val[root[i]] + j << " ";
        }
    }*/
}