[POI2007]ZAP-Queries 数学

题目描述

Byteasar the Cryptographer works on breaking the code of BSA (Byteotian Security Agency). He has alreadyfound out that whilst deciphering a message he will have to answer multiple queries of the form"for givenintegers aaa, bbb and ddd, find the number of integer pairs (x,y)(x,y)(x,y) satisfying the following conditions:

1≤x≤a1\le x\le a1≤x≤a,1≤y≤b1\le y\le b1≤y≤b,gcd(x,y)=dgcd(x,y)=dgcd(x,y)=d, where gcd(x,y)gcd(x,y)gcd(x,y) is the greatest common divisor of xxx and yyy".

Byteasar would like to automate his work, so he has asked for your help.

TaskWrite a programme which:

reads from the standard input a list of queries, which the Byteasar has to give answer to, calculates answers to the queries, writes the outcome to the standard output.

FGD正在破解一段密码，他需要回答很多类似的问题：对于给定的整数a,b和d，有多少正整数对x,y，满足x<=a，y<=b，并且gcd(x,y)=d。作为FGD的同学，FGD希望得到你的帮助。

输入输出格式

输入格式：

The first line of the standard input contains one integer nnn (1≤n≤50 0001\le n\le 50\ 0001≤n≤50 000),denoting the number of queries.

The following nnn lines contain three integers each: aaa, bbb and ddd(1≤d≤a,b≤50 0001\le d\le a,b\le 50\ 0001≤d≤a,b≤50 000), separated by single spaces.

Each triplet denotes a single query.

输出格式：

Your programme should write nnn lines to the standard output. The iii'th line should contain a single integer: theanswer to the iii'th query from the standard input.

输入输出样例

输入样例#1：
复制

输出样例#1： 复制

3

2

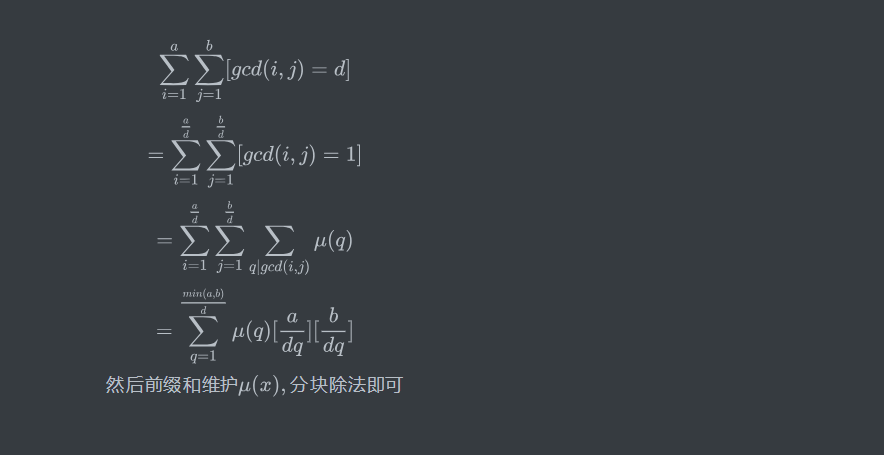
#include<iostream>

#include<cstdio>

#include<algorithm>

#include<cstdlib>

#include<cstring>

#include<string>

#include<cmath>

#include<map>

#include<set>

#include<vector>

#include<queue>

#include<bitset>

#include<ctime>

#include<time.h>

#include<deque>

#include<stack>

#include<functional>

#include<sstream>

//#include<cctype>

//#pragma GCC optimize(2)

using namespace std;

#define maxn 200005

#define inf 0x7fffffff

//#define INF 1e18

#define rdint(x) scanf("%d",&x)

#define rdllt(x) scanf("%lld",&x)

#define rdult(x) scanf("%lu",&x)

#define rdlf(x) scanf("%lf",&x)

#define rdstr(x) scanf("%s",x)

#define mclr(x,a) memset((x),a,sizeof(x))

typedef long long  ll;

typedef unsigned long long ull;

typedef unsigned int U;

#define ms(x) memset((x),0,sizeof(x))

const long long int mod = 98765431;

#define Mod 1000000000

#define sq(x) (x)*(x)

#define eps 1e-5

typedef pair<int, int> pii;

#define pi acos(-1.0)

//const int N = 1005;

#define REP(i,n) for(int i=0;i<(n);i++)

typedef pair<int, int> pii;

inline int rd() {

	int x = 0;

	char c = getchar();

	bool f = false;

	while (!isdigit(c)) {

		if (c == '-') f = true;

		c = getchar();

	}

	while (isdigit(c)) {

		x = (x << 1) + (x << 3) + (c ^ 48);

		c = getchar();

	}

	return f ? -x : x;

}

ll gcd(ll a, ll b) {

	return b == 0 ? a : gcd(b, a%b);

}

int sqr(int x) { return x * x; }

/*ll ans;

ll exgcd(ll a, ll b, ll &x, ll &y) {

	if (!b) {

		x = 1; y = 0; return a;

	}

	ans = exgcd(b, a%b, x, y);

	ll t = x; x = y; y = t - a / b * y;

	return ans;

}

*/

int n;

int mu[maxn+10], vis[maxn+10];

int sum[maxn + 10];

void init() {

	for (int i = 1; i < maxn; i++)mu[i] = 1, vis[i] = 0;

	for (int i = 2; i < maxn; i++) {

		if (vis[i])continue;

		mu[i] = -1;

		for (int j = 2 * i; j < maxn; j += i) {

			vis[j] = 1;

			if ((j / i) % i == 0)mu[j] = 0;

			else mu[j] *= -1;

		}

	}

	for (int i = 1; i < maxn; i++)sum[i] = sum[i - 1] + mu[i];

}

int main()

{

	//	ios::sync_with_stdio(0);

	init();

	n = rd();

	while (n--) {

		int a = rd(), b = rd(), d = rd();

		ll ans = 0;

		for (int l = 1, r; l <= (min(a, b) / d); l = r + 1) {

			r = min((a / d) / (a / d / l), (b / d) / (b / d / l));

			ans += 1ll * (sum[r] - sum[l - 1])*(a / d / l)*(b / d / l);

		}

		cout << (ll)ans << endl;

	}

	return 0;

}