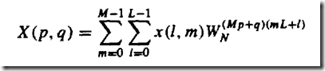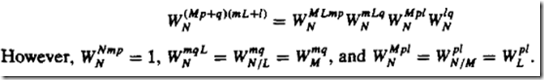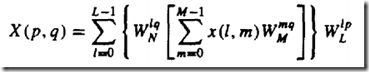DFT到FFT的理解
DFT简化计算理解(FFT)
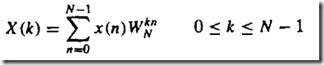
DFT: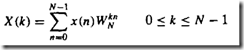
WN=e^(-j*2*pi/N)
DFT复杂度o(N^2)
降低与N^2的依赖 使N = LM (L^2+m^2 <= N^2)
N点DFT分解为M段L点DFT
一维的N点序列变为(L,M)二维序列,每一行分别进行DFT
举例两种一维到二维的映射关系
n = Ml+m
| 1 | 3 | 5 | 7 | 9 |
| 2 | 4 | 6 | 8 | 10 |
n = l+mL
| 1 | 2 | 3 | 4 | 5 |
| 6 | 7 | 8 | 9 | 10 |
与之所求的DFT 也可存入相对应的(q,p)矩阵中
以第一种(n = Ml+m)为例:k = Mp+q
找书麻烦这里给出推到:
重一维到二维
两种流程:

按列存入信号
计算每行M点DFT
乘以相位因子
计算每一列的L点DFT
按行读取所得数组

图示:
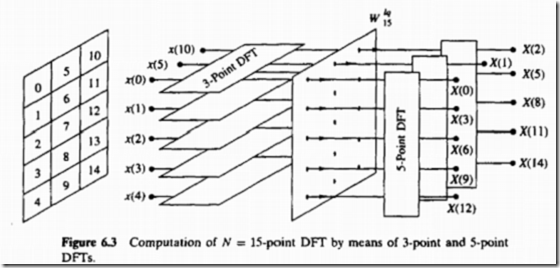
来看下基2_FFT算法:
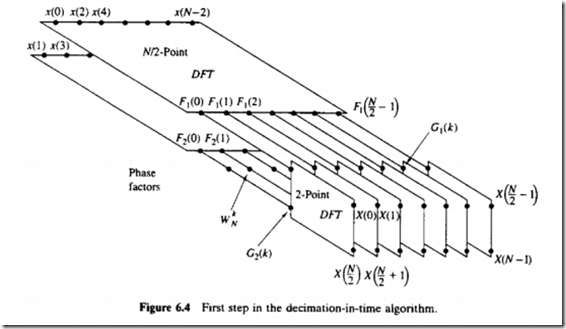
上图的N/2点的dft可以分解为N/4的而N/4的DFT可以分解为N/8的……直到最后分解为2点的DFT
这儿的2点DFT其实是输出A+B,A-B两个值
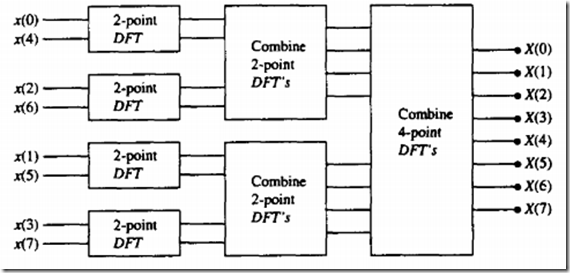
为什么可以这样分解呢?其实他就是1个数学式子的’分解‘过程,来看下
N点的DFT是这玩意儿
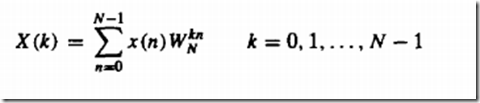
将序列 奇偶分开
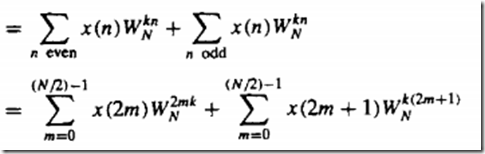
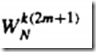 拆开成2km与1两项
拆开成2km与1两项
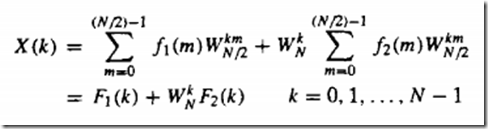
X(2m) 可看为f(m)
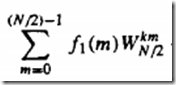 而这个可看作一个新的N/2点DFT ------------可见N点的DFT已经分解为N/2点DFT
而这个可看作一个新的N/2点DFT ------------可见N点的DFT已经分解为N/2点DFT

由采样定理,在频域上(N/2以为新的周期)F(k+N/2)=F(k),且,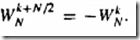 。
。
所以得出下式:
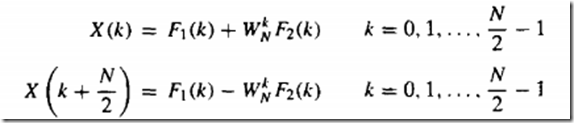
复数乘法运算量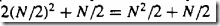 。而原始DFtT的量为N^2,当N够大时几乎减小了一半
。而原始DFtT的量为N^2,当N够大时几乎减小了一半
注意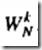 的确定,他是
的确定,他是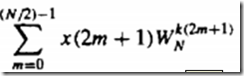 分解出来的
分解出来的
这是举例看下8点DFT的奇偶分解
| 一级dft(抽第二级奇偶) | 二级dft(抽第三极的奇偶) | 第三极dft(最终) |
| 0 | 0 | 0 |
| 4 | 2 | 1 |
| 2 | 4 | 2 |
| 6 | 6 | 3 |
| 1 | 1 | 4 |
| 5 | 3 | 5 |
| 3 | 5 | 6 |
| 7 | 7 | 7 |
可用二进制倒序实现 即011100变为001110,感觉镜像啦下
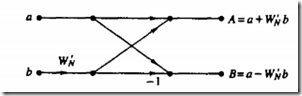 对比下
对比下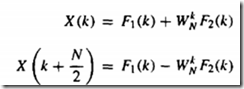
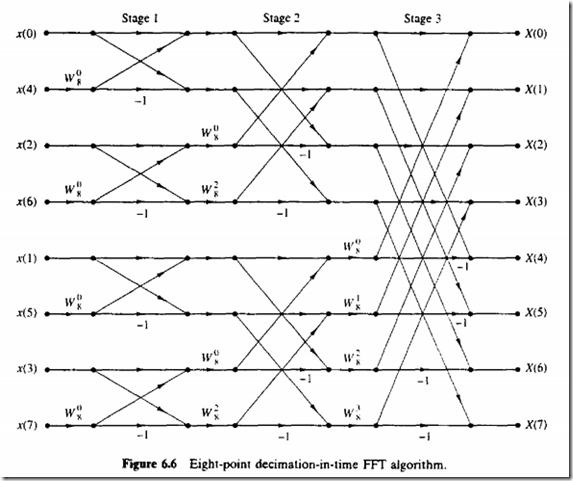
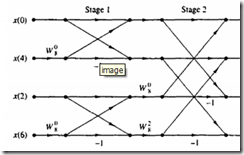 可看作一个4点DFT,只需求k=0,1的DFT,即可根据关系得出k=2,3
可看作一个4点DFT,只需求k=0,1的DFT,即可根据关系得出k=2,3
第二级 等于W(4,0),W(1,4)
等于W(4,0),W(1,4)
DFT到FFT的理解的更多相关文章
- FS,FT,DFS,DTFT,DFT,FFT的联系和区别
DCT变换的原理及算法 文库介绍 对于初学数字信号处理(DSP)的人来说,这几种变换是最为头疼的,它们是数字信号处理的理论基础,贯穿整个信号的处理. 学习过<高等数学>和<信号与系统 ...
- 一个蒟蒻对FFT的理解(蒟蒻也能看懂的FFT)
建议同学们先自学一下"复数(虚数)"的性质.运算等知识,不然看这篇文章有很大概率看不懂. 前言 作为一个典型的蒟蒻,别人的博客都看不懂,只好自己写一篇了. 膜拜机房大佬 HY 一. ...
- Matlab 之 FFT的理解和应用
网上看了一些大牛的关于FFT的见解,加上自己的一点儿理解,针对以下这几个问题来加深对FFT的理解. 不知道大家有没有类似以下几点的困惑: 问题的提出 对于1秒钟输出的连续信号,使用采样率Fs不同,就会 ...
- FS,FT,DFS,DTFT,DFT,FFT的联系和区别 数字信号处理
DCT变换的原理及算法 文库介绍 对于初学数字信号处理(DSP)的人来说,这几种变换是最为头疼的,它们是数字信号处理的理论基础,贯穿整个信号的处理. 学习过<高等数学>和<信号与系统 ...
- [信号与系统]傅里叶变换、DFT、FFT分析与理解
目录 一.前言 二.傅里叶变换 1.傅里叶级数 2.傅里叶级数系数求解 2.1.求解方法 2.2.三角函数的正交性 2.3.系数求解过程 2.4.关于傅里叶级数的个人感悟 3.引入复指数 4.总结 三 ...
- FFT算法理解与c语言的实现
完整内容迁移至 http://www.face2ai.com/DIP-2-3-FFT算法理解与c语言的实现/ http://www.tony4ai.com/DIP-2-3-FFT算法理解与c语言的实现 ...
- 【总结】对FFT的理解 / 【洛谷 P3803】 【模板】多项式乘法(FFT)
题目链接 \(\Huge\text{无图,慎入}\) \(FFT\)即快速傅里叶变换,用于加速多项式乘法. 如果暴力做卷积的话就是一个多项式的每个单项式去乘另一个多项式然后加起来,时间复杂度为\(O( ...
- DTFT、DFT、FFT
对于一般的周期信号可以用一系列(有限个或者无穷多了)正弦波的叠加来表示.这些正弦波的频率都是某一个特定频率的倍数如5hz.2*5hz.3*5hz--(其中的 5hz 叫基频).这是傅立叶级数的思想.所 ...
- 【转】离散傅里叶变换-DFT(FFT)基础
转:https://blog.csdn.net/zhangxz259/article/details/81627341 什么是离散傅里叶变换 matlab例子 本文是从最基础的知识开始讲解,力求用最通 ...
随机推荐
- Java-Runoob:Java 开发环境配置
ylbtech-Java-Runoob:Java 开发环境配置 1.返回顶部 1. Java 开发环境配置 在本章节中我们将为大家介绍如何搭建Java开发环境. Windows 上安装开发环境 Lin ...
- JAVA基础知识——IO
首先看一下JAVA IO的类继承关系
- STL的一些技巧函数使用
1.emplace() 函数和 emplace_back() 函数 C++11的STL中新增加了emplace() 函数和 emplace_back() 函数,用来实现insert() 函数和 pus ...
- Windows可信任路径代码执行漏洞
乌云里有很多这样的案例,当然在开发过程中也会存在这样的问题 搜索:可信任路径漏洞 调用案例中的描述: Microsoft Windows API使用CreateProcess()函数创建新的进程及其主 ...
- Halcon学习之边缘检测函数
sobel_amp ( Image : EdgeAmplitude : FilterType, Size : ) 根据图像的一次导数计算图像的边缘 close_edges ( Edges, EdgeI ...
- 无法安装 Microsoft Visual Studio 2010 Service Pack 1
解决办法: 32 位系统删除:HKEY_LOCAL_MACHINE\Software\Microsoft\VSTO Designtime Setup\ 64 位系统删除:HKEY_LOCAL_MACH ...
- Elasticsearch之kopf插件安装之后的浏览详解
前提, Elasticsearch之插件介绍及安装 https://i.cnblogs.com/posts?categoryid=950999&page=2 (强烈建议,从头开始看) 比如, ...
- MySQL分组条件,group by order by limit 顺序
having 中如果没有用聚合函数(必须sum,min),涉及到的字段名称必须在select 中有对应字段名称才可以,用到聚合函数可以不必在select中有相应字段名称的 limit 2,3:2表示从 ...
- Timer的定义及demo
- Project Browser & Inspector
[Project Browser] You can drag items from the project structure list to the Favourites and also save ...