[排序算法] 希尔排序 (C++)

前言

本文章是建立在插入排序的基础上写的喔，如果有对插入排序还有不懂的童鞋，可以看看这里。

直接/折半插入排序 2路插入排序

---

希尔排序解释

希尔排序 Shell Sort 又名"缩小增量排序"，是对直接插入排序更加高效的改进版本。它是由 Donald Shell 于1959年提出的一种排序算法。

希尔排序 其原理是设置一个增量incre，在原序列上每隔一个增量选取一个数据元素，将这些选取的元素构造成一个子序列。

每设一个增量，我们每次会得到一组子序列 (子序列个数和当前增量相等)，然后分别对这些子序列进行 直接插入排序 。

随着增量的减少，重复上述的操作，直到增量incre为 1 时，最后完成整个序列的排序。

---

希尔排序增量的选取

原始希尔增量

对于 希尔排序 的增量的选取，Donald Shell 一开始提出增量每次为上次的 1/2。

也就是说，若数组长度为n，一开始增量为 n/2，之后每次增量都取上次的 1/2。

Knuth序列

Knuth序列：以逆向形式从1开始，通过递归表达式 interval = 3 * interval + 1 来产生，以此来得到间隔大小。

由此我们可以得到如下的增量选取方式:

具体方法是若数组长度为n，一开始增量取 n/3 向下取整 + 1。然后每次都取上次的增量的 1/3向下取整 + 1。

当n足够大时，使用 Knuth序列 得到的增量选取方式，可以一定程度上提高希尔排序的效率。

(上面说的东西其实我也不知道对不对，至于为什么这样取，我也不知道哇哇哇 )

(在后文的程序中，我会采取此方式选取增量。）

---

希尔排序动态演示

我们以 [6,5,2,4,1,3] 为例进行动态演示

第一次取增量，构造一组子序列

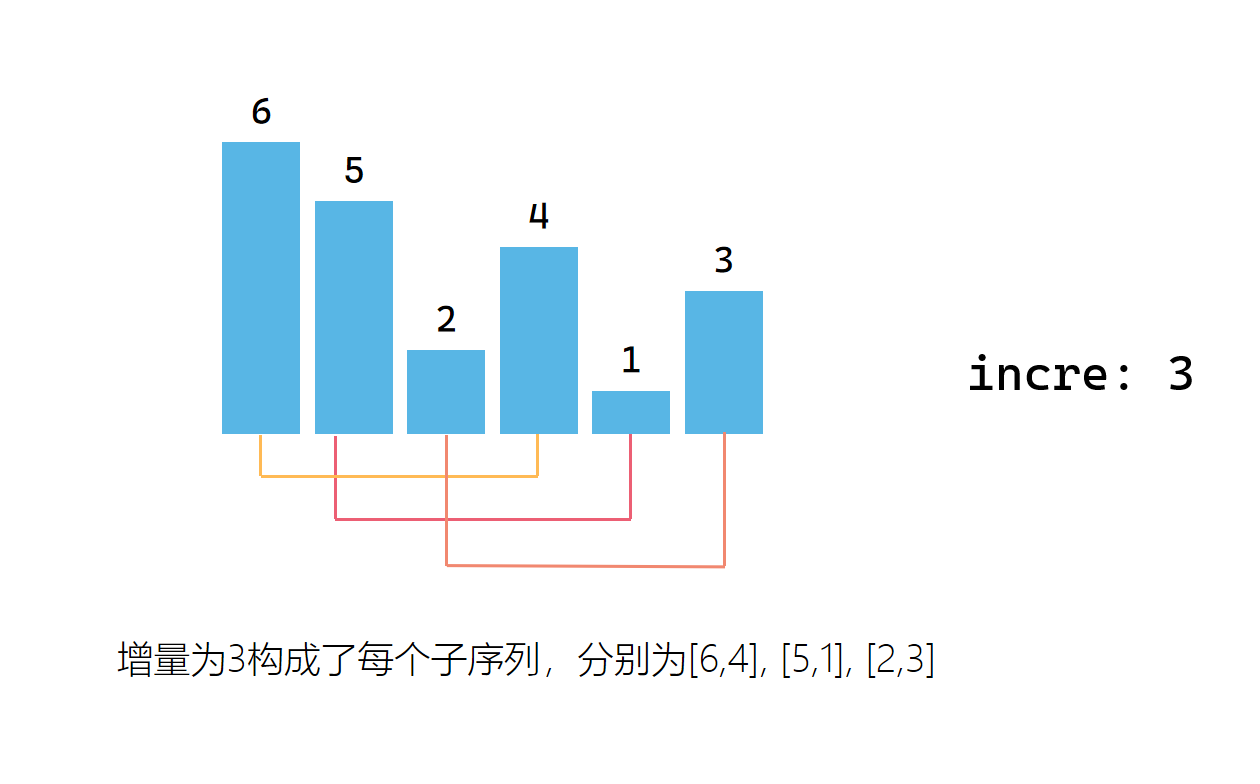
第一次取增量后，对每个子序列进行直接插入排序

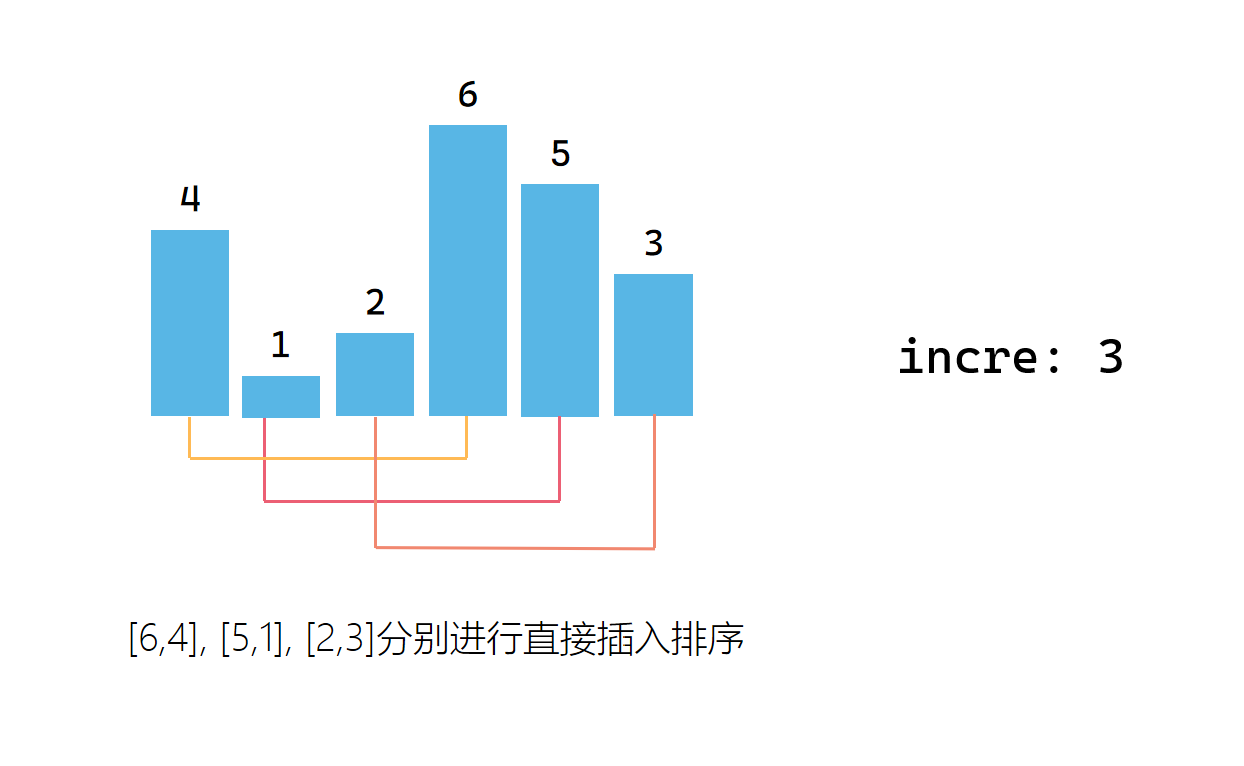
第二次取增量，构造一组子序列

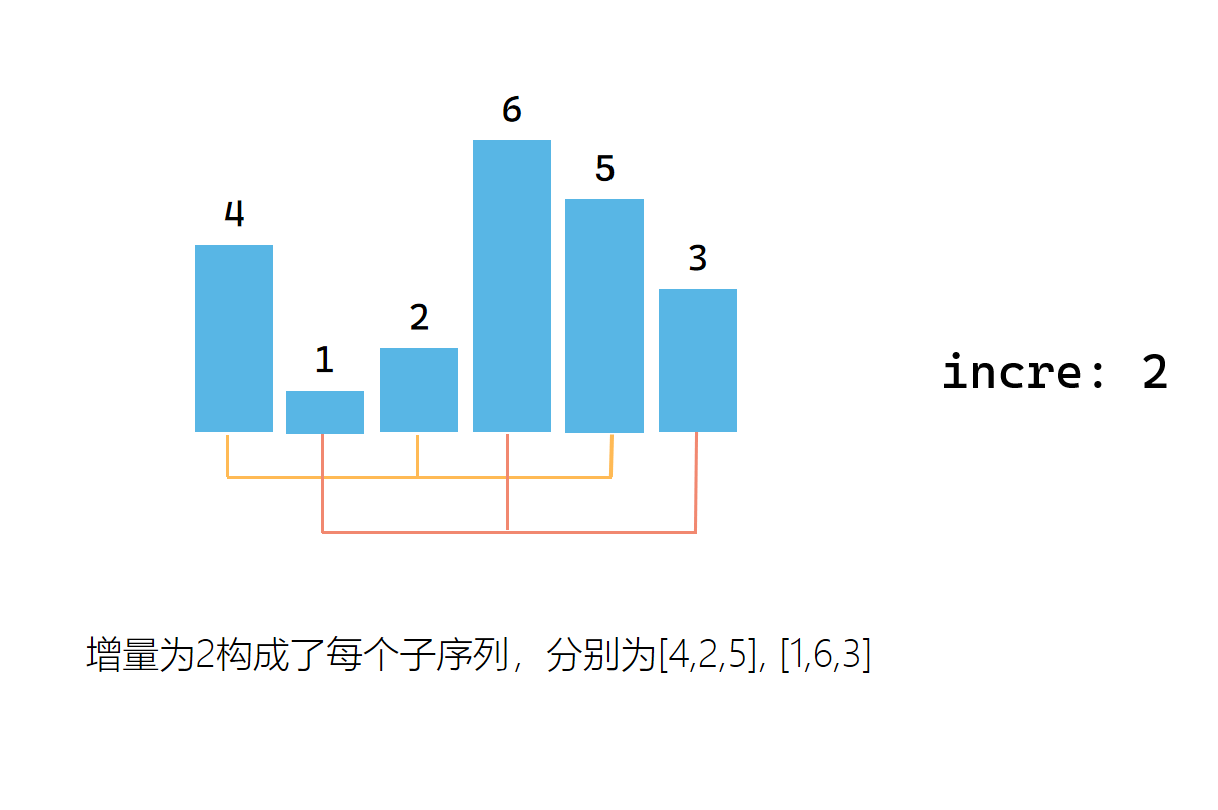
第二次取增量后，对每个子序列进行直接插入排序

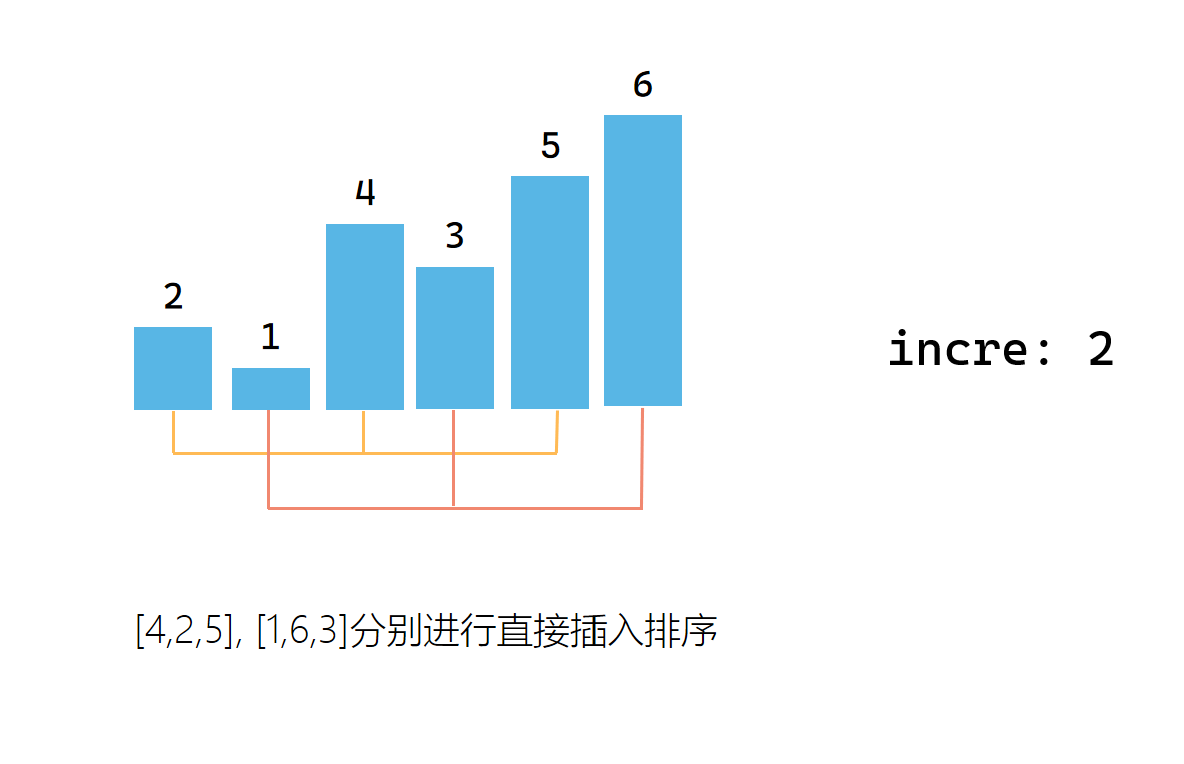
第三次取增量，构造一组子序列

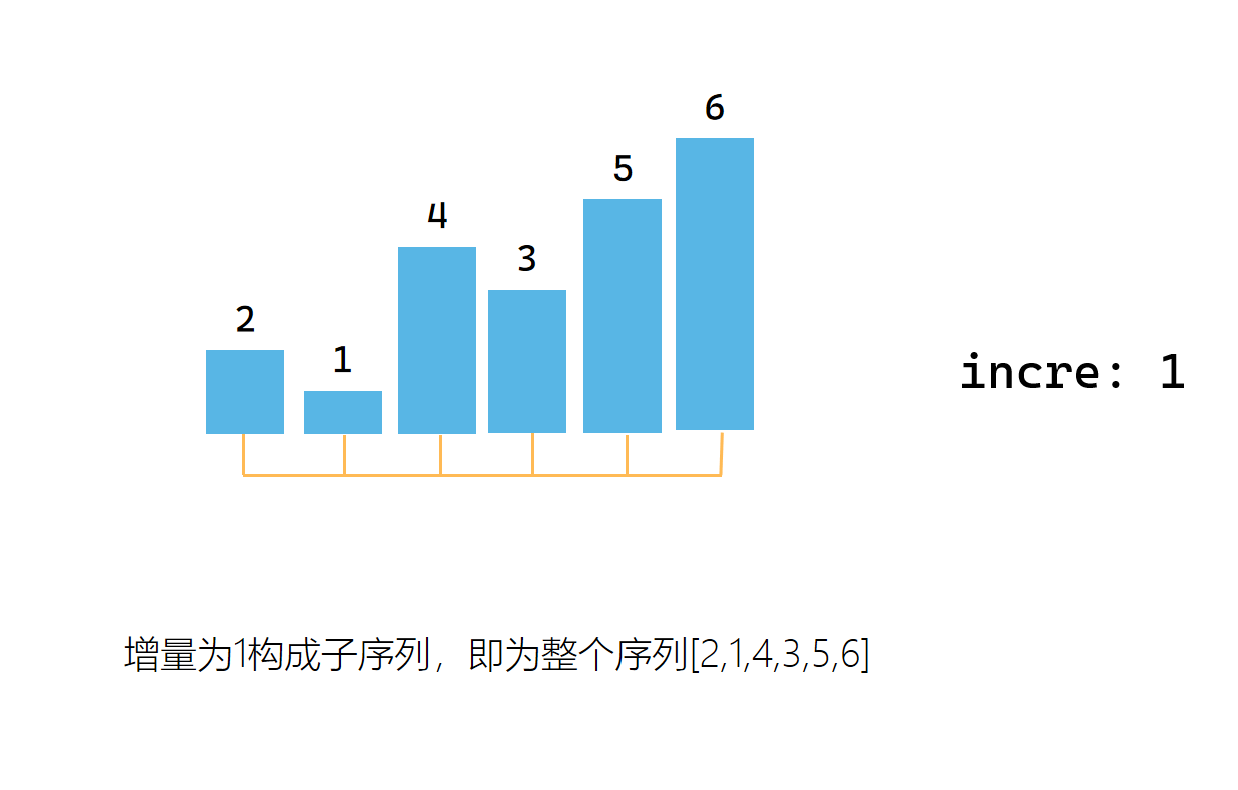
第三次取增量后，对每个子序列进行直接插入排序

---

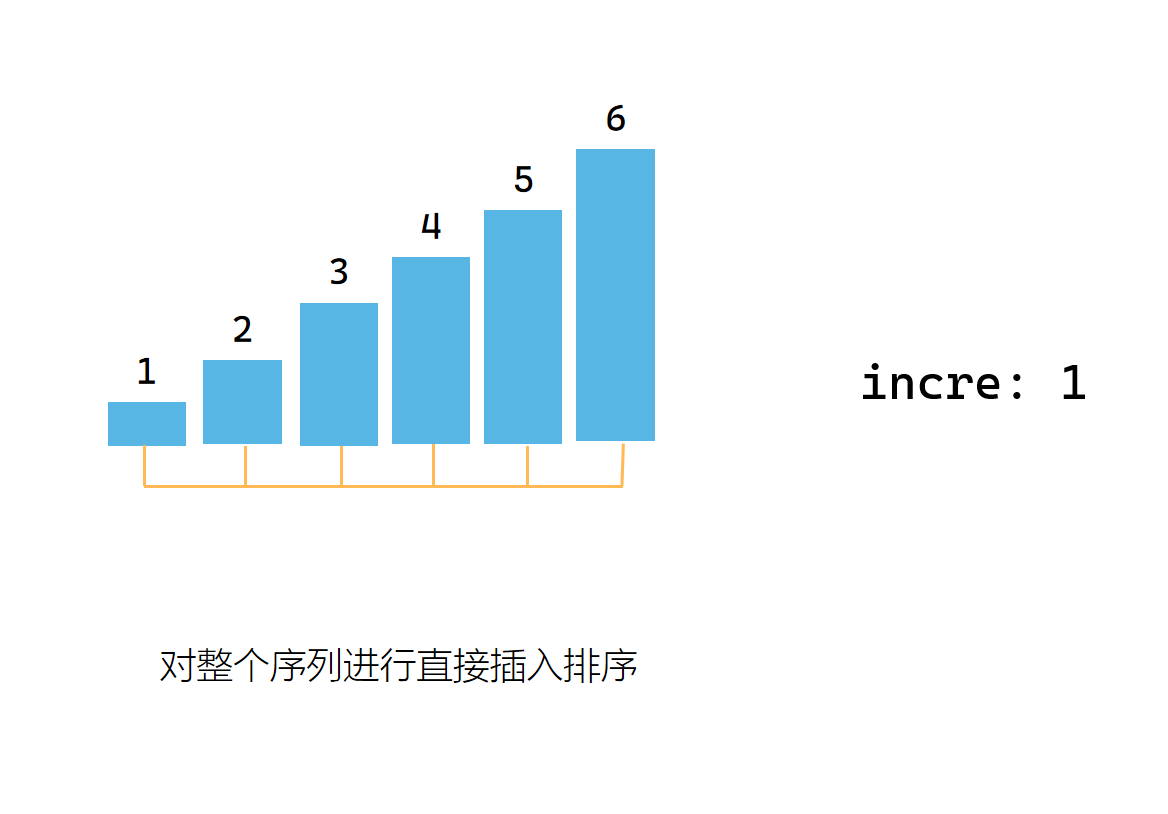
希尔排序时间复杂度

对于 希尔排序 的时间复杂度，我真的研究了好久，用尽自己毕生所学的高数知识。

但是能力有限，最终没有探索出什么结果呜呜呜(是我太菜了对不起)

不过有人通过大量的实验，给出了较好的结果：当n较大时，比较和移动的次数约在 n^1.25 到 (1.6n)^1.25 之间。

---

希尔排序核心代码

//设置增量  每隔一个增量取一个数 组成长度相同的子序列
void ShellSort(vector<int> &v){
    int n = v.size();
    int incre = n;                       //初始化增量
    while(incre > 1){                    //最后一次增量为1
	incre = incre / 3 + 1;           //除三向下取整加一
	//(至于为什么这样取, 哇咖喱嘛三)
	for(int i = incre; i < n; i++){
	    int key = v[i];              //当前需要插入的数
	    int j = i - incre;
	    while(j >= 0 && v[j] > key){
		v[j + incre] = v[j];
		j -= incre;              //对每个子序列进行直接插入排序
	    }
	    v[j + incre] = key;          //插入到合适位置
	}
    }
}

---

完整程序源代码

#include<iostream>
#include<vector>
#include<time.h>
using namespace std;

//设置增量  每隔一个增量取一个数 组成长度相同的子序列
void ShellSort(vector<int> &v){
    int n = v.size();
    int incre = n;                       //初始化增量
    while(incre > 1){                    //最后一次增量为1
        incre = incre / 3 + 1;           //除三向下取整加一
	//(至于为什么这样取, 哇咖喱嘛三)
	for(int i = incre; i < n; i++){
	    int key = v[i];              //当前需要插入的数
	    int j = i - incre;
	    while(j >= 0 && v[j] > key){
		v[j + incre] = v[j];
		j -= incre;              //对每个子序列进行直接插入排序
	    }
	    v[j + incre] = key;          //插入到合适位置
	}
    }
}

void show(vector<int> &v){
    for(auto &x : v)
	cout<<x<<" ";
    cout<<endl;
}

main(){
    vector<int> v;
    int n = 50;
    srand((int)time(0));
    while(n--)
	v.push_back(rand() % 100 + 1);

    show(v);

    ShellSort(v);

    cout<<endl<<endl;
    show(v);
}

---

程序运行结果图