3.对互斥事件和条件概率的相互理解《zobol的考研概率论教程》

tag:这篇文章没太多思考的地方，就是做个过渡

1.从条件概率来定义互斥和对立事件

2.互斥事件是独立事件吗？

3.每个样本点都可以看作是互斥事件，来重新看待条件概率

一、从条件概率来定义互斥和对立事件

根据古典概率-条件概率的定义，当在“A的样本点集合中，没有一个B集合中的样本点”的时候：

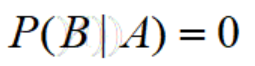
则A、B事件构成了一对互斥事件，简单理解就是发生了A就绝对不可能发生B，又根据条件概率的展开式，我们可以推出常见的两个公式：

互斥事件在V-N图上来看，就是两个事件的集合没有交集。

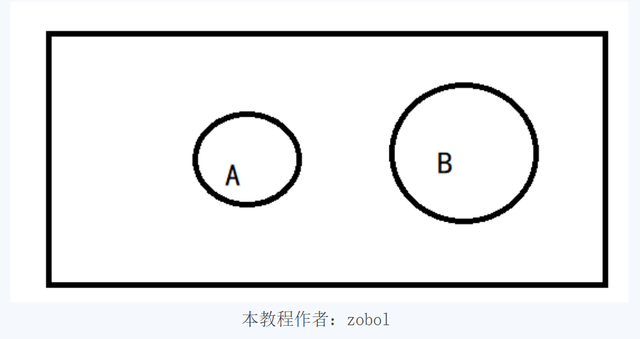
二.互斥事件是独立事件吗？

互斥事件不仅不是独立事件，还是一种关系十分紧密的事件，它的关系是“如果A发生，则B一定不发生”，这是可谓是你死我活般的关系。

独立事件的意思是“A的发生对B的发生概率值没有任何影响”，这不仅仅有影响还给全面否定了。

三.每个样本点都可以看作是互斥事件，来重新看待条件概率

因为每个样本点之间都是没有任何交集的，所以各个样本点之间都是互斥事件。

（1）A事件的发生=A集合中的任意一个样本点发生。

（2）由互斥事件含义，A集合外的任意一个样本点都不可能发生。

（3）在条件A的约束下，我们不可能选择到A集合外的样本点。

（4）也就是说我们只能从A集合中任意选择一个点

（5）如果选择的是样本点也在B集合中，那么就是P(B|A)

由此我们推出从互斥事件的角度来理解的条件概率的公式：

 

如果我的教程对您有帮助,欢迎关注我的博客：

主博客：https://zobolblog.github.io/ProbabilityTheory/

B站：喜欢数学的zobol

讨论群：154390881

个人公众号：zobol的魔法藏书室

博客园：https://www.cnblogs.com/zobol/

csdn: https://blog.csdn.net/zobol_world

知乎：https://www.zhihu.com/people/zobol

今日头条：喜欢数学的zobol

百家号：zobol的魔法藏书室