【题解】CF1714F Build a Tree and That Is It

题面传送门

解决思路

题目中虽然说是无根树，但我们可以钦定这棵树的根为节点 \(1\)，方便构造，这是不

影响结果的。

以下记给定的三段长度为 \(a,b,c\)。

先考虑无解的情况。

• 首先，给出的三个距离，任意两者之和必须大于等于第三者，否则显然无解。

• 其次，用到的边数不能 \(\ge n\)。

• 最后，两个节点的 \(\text{LCA}\) 到根节点的距离 (绿色) 是整数，两节点之间最短距离 (蓝色) 也是整数，而 \(a+b+c\) 正好是蓝色绿色各算两次，所以 \(a+b+c\) 必须是偶数。

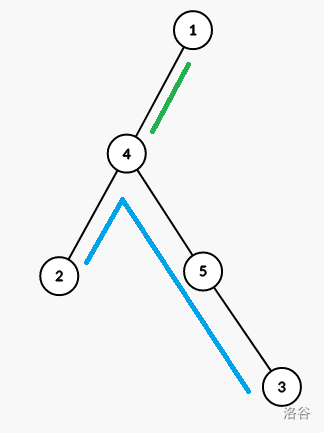
然后考虑如何构造。

为了方便，我们钦定节点 \(2\) 离根节点距离较小的一个。可以事先比较并做交换，输出时修改一下。

一种比较简单的想法：

给一组例子：

10 5 5 4

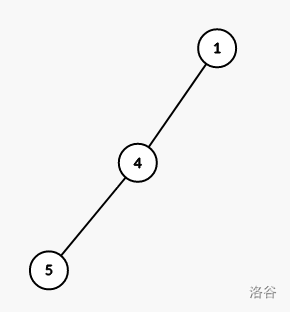
首先把节点 \(2\) 和节点 \(3\) 可以公共的部分输出。公共祖先数 (不包括节点 \(1\) ) 可以这样

算: \((a+c-b)/2\)（想一想为什么）。输出的 \(now\)（当前填充节点）应该从节点 \(4\) 开始，\(lst\)（上一个节点）初始设为节点 \(1\)，之后每一次将 \(lst\) 更新为 \(now\)，然后将 \(now +1\)。

处理完会变成这样：

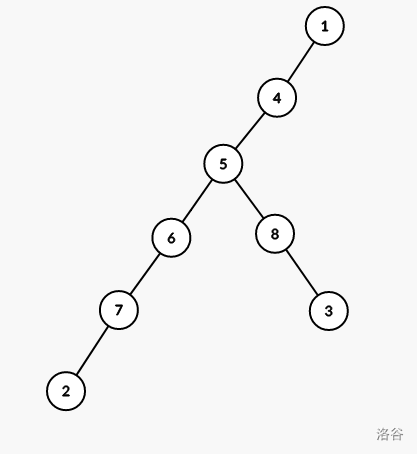
然后从当前扩展到的节点分别向两侧延伸，记已经输出的公共祖先数为 \(cnt\)，那么节点 \(2\) 还需拓展的点数为 \(a-cnt-1\)，节点 \(3\) 还需拓展的点数为 \(b-(a-cnt)-1\)。像之前一样分别向两边拓展即可。注意拓展节点 \(2\) 之前先把 \(lst\) 暂存下来，方便之后拓展节点 \(3\) 时将 \(lst\) 归位。

处理完会变成这样：

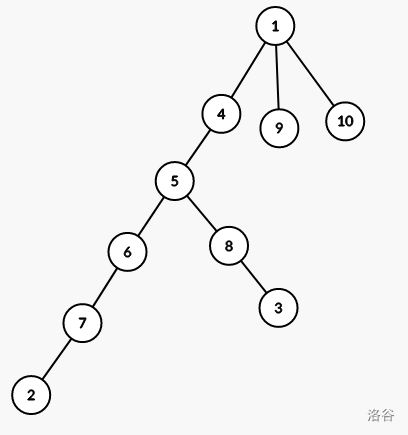
最后还剩的点全部连到节点 \(1\) 上即可（连其他地方也没事）。

所以这个样例最后一组可行的解就是这样：

先给出这一部分的代码：

int _1=2,_2=3;
if(a>c){
	swap(a,c);
	swap(_1,_2);
}
int lst=1,now=4,cnt=0;
for(int i=1;i<=(a+c-b)/2;i++){
	cout<<lst<<' '<<now<<endl;
	lst=now,now++,cnt++;
}
a-=cnt,c-=cnt;
int t1=lst;
for(int i=1;i<a;i++){
	cout<<lst<<' '<<now<<endl;
	lst=now,now++;
}
cout<<lst<<' '<<_1<<endl;
lst=t1;
for(int i=1;i<b-a;i++){
	cout<<lst<<' '<<now<<endl;
	lst=now,now++;
}
cout<<lst<<' '<<_2<<endl;
for(int i=now;i<=n;i++) cout<<1<<' '<<i<<endl;

然而这样写却 \(\text{WA}\) 了。对照错误样例 通过仔细思考，我们可以发现一种特殊情况，比如：

6 2 3 5

这时，以上的程序给出了一个离谱的错误答案。手玩发现，这种特殊情况是整棵树恰好为一条链：

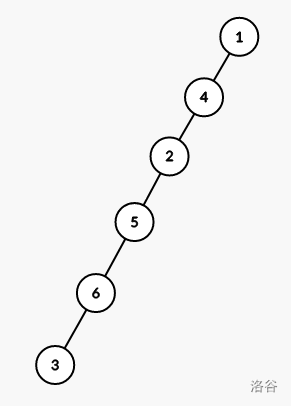
这时，较近的点为较远的点的祖先，也就是 \(a+b=c\)。

所以，只需要特判出来，按照链的特点，用类似方法构造即可。

AC Code

#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(false)
#define TIE cin.tie(0),cout.tie(0)
using namespace std;
int T,n,a,b,c,d1,d2,d3;
void solve(){
	cin>>n>>a>>b>>c;
	d1=(a+c-b)/2;
	d2=(a+b-c)/2;
	d3=(b+c-a)/2;
	if(d1<0||d2<0||d3<0||d1+d2+d3>=n||(a+b+c)%2){
		cout<<"NO"<<endl;
		return ;
	}
	cout<<"YES"<<endl;
	int _1=2,_2=3;
	if(a>c){
		swap(a,c);
		swap(_1,_2);
	}
	int lst=1,now=4,cnt=0;
	if(a+b==c){
		for(int i=1;i<a;i++){
			cout<<lst<<' '<<now<<endl;
			lst=now,now++;
		}
		cout<<lst<<' '<<_1<<endl;
		lst=_1;
		for(int i=1;i<b;i++){
			cout<<lst<<' '<<now<<endl;
			lst=now,now++;
		}
		cout<<lst<<' '<<_2<<endl;
	}
	else{
		for(int i=1;i<=(a+c-b)/2;i++){
			cout<<lst<<' '<<now<<endl;
			lst=now,now++,cnt++;
		}
		a-=cnt,c-=cnt;
		int t1=lst;
		for(int i=1;i<a;i++){
			cout<<lst<<' '<<now<<endl;
			lst=now,now++;
		}
		cout<<lst<<' '<<_1<<endl;
		lst=t1;
		for(int i=1;i<b-a;i++){
			cout<<lst<<' '<<now<<endl;
			lst=now,now++;
		}
		cout<<lst<<' '<<_2<<endl;
	}
	for(int i=now;i<=n;i++) cout<<1<<' '<<i<<endl;
}
int main(){
	IOS;TIE;
	cin>>T;
	while(T--) solve();
	return 0;
}