运筹学之"简单平均预测法"和"加权滑动平均预测法"和"确定平滑系数"
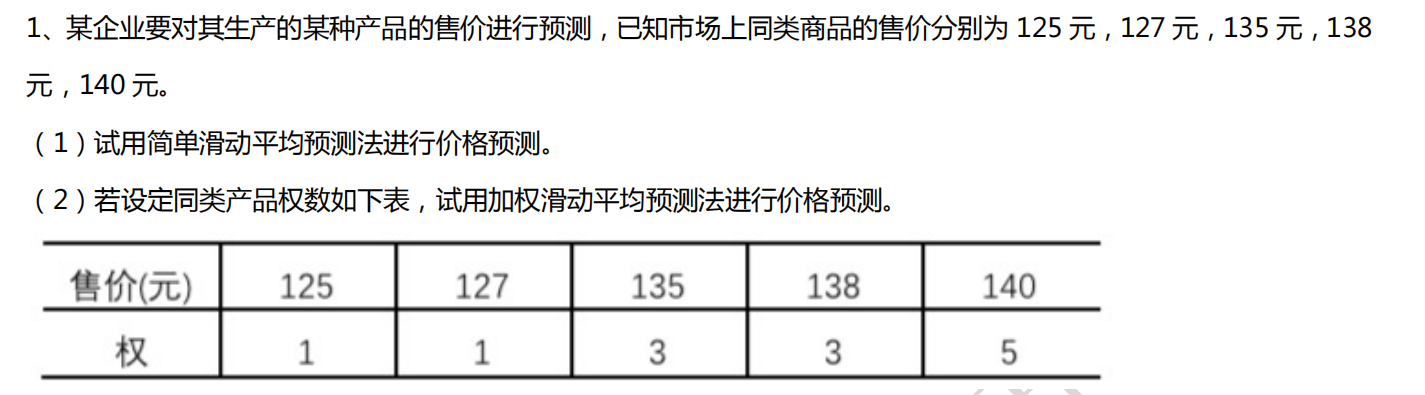
1.简单滑动平均预测法就是将所有的售价加起来除以总数
665/5=133
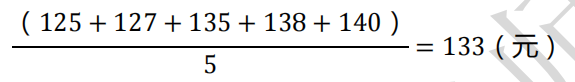
2.加权滑动平均预测法:需要将售价分别乘以权之和,并除以权之和
1771/13≈136.23
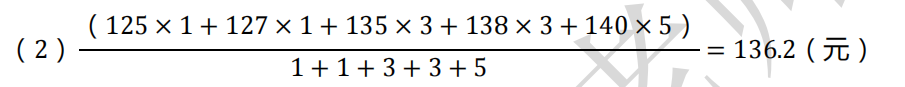
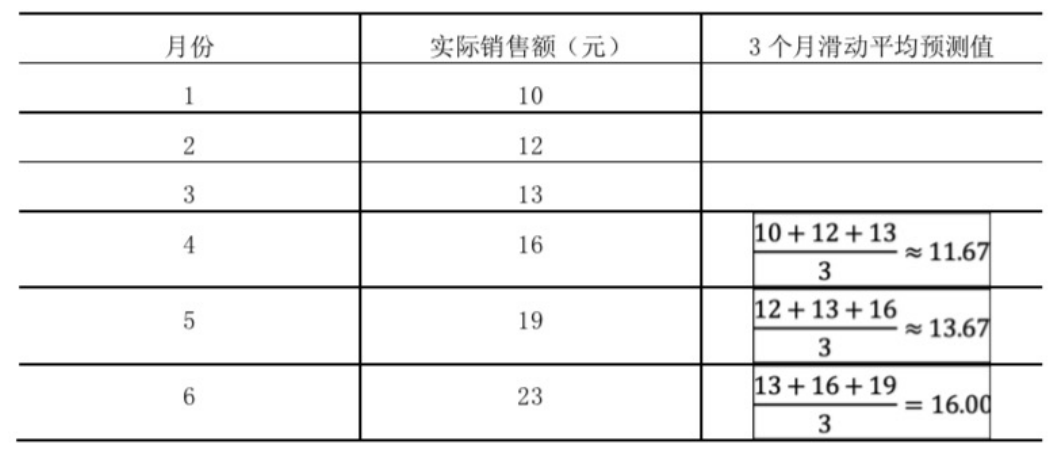
二、某木材公司销售房架构件,其中某种配件的销售数据如下表。试计算:3 个月的简单滑动平均预测值(计算结果直接填在表中相应空格)。
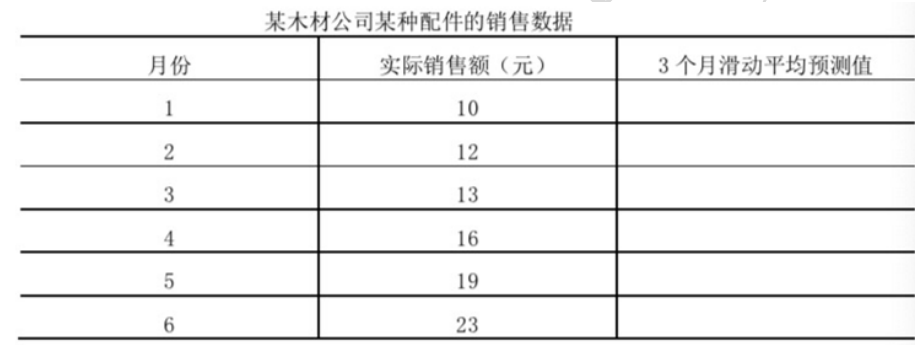
答:123 月滑动预测 4 月,234 月滑动预测 5 月,345 月滑动预测 6 月。
三、设某商品第 t 期实际价格为 500 元,用指数平滑法得到第 t 期预测价格为 480 元,第 t+1 期预测价格为 488 元。
(1)试确定平滑系数。
(2)若商品价格是看涨的,选取的平滑系数是否合理?应如何选取平滑系数?
解题思路:
t+1预测价格 = 平滑系数 t实际价格 + ( 1 - 平滑系数 ) t预测价格 = Ft+1 = a Xt + (1 - a)Ft
参数解析:
Ft是t预测值:480
Ft+1是t+1预测值:488
a是平滑系数:未知数
Xt是t实际价值:500
答案:

运筹学之"简单平均预测法"和"加权滑动平均预测法"和"确定平滑系数"的更多相关文章
- 理解滑动平均(exponential moving average)
1. 用滑动平均估计局部均值 滑动平均(exponential moving average),或者叫做指数加权平均(exponentially weighted moving average),可以 ...
- (转)理解滑动平均(exponential moving average)
转自:理解滑动平均(exponential moving average) 1. 用滑动平均估计局部均值 滑动平均(exponential moving average),或者叫做指数加权平均(exp ...
- 简单的java Hadoop MapReduce程序(计算平均成绩)从打包到提交及运行
[TOC] 简单的java Hadoop MapReduce程序(计算平均成绩)从打包到提交及运行 程序源码 import java.io.IOException; import java.util. ...
- Tensorflow滑动平均模型tf.train.ExponentialMovingAverage解析
觉得有用的话,欢迎一起讨论相互学习~Follow Me 移动平均法相关知识 移动平均法又称滑动平均法.滑动平均模型法(Moving average,MA) 什么是移动平均法 移动平均法是用一组最近的实 ...
- [开发技巧]·Python极简实现滑动平均滤波(基于Numpy.convolve)
[开发技巧]·Python极简实现滑动平均滤波(基于Numpy.convolve) 1.滑动平均概念 滑动平均滤波法(又称递推平均滤波法),时把连续取N个采样值看成一个队列 ,队列的长度固定为N ...
- 『TensorFlow』滑动平均
滑动平均会为目标变量维护一个影子变量,影子变量不影响原变量的更新维护,但是在测试或者实际预测过程中(非训练时),使用影子变量代替原变量. 1.滑动平均求解对象初始化 ema = tf.train.Ex ...
- Tensorflow中的滑动平均模型
原文链接 在Tensorflow的教程里面,使用梯度下降算法训练神经网络时,都会提到一个使模型更加健壮的策略,即滑动平均模型. 基本思想 在使用梯度下降算法训练模型时,每次更新权重时,为每个权重维护一 ...
- TensorFlow+实战Google深度学习框架学习笔记(11)-----Mnist识别【采用滑动平均,双层神经网络】
模型:双层神经网络 [一层隐藏层.一层输出层]隐藏层输出用relu函数,输出层输出用softmax函数 过程: 设置参数 滑动平均的辅助函数 训练函数 x,y的占位,w1,b1,w2,b2的初始化 前 ...
- 孙子兵法的计是最早的SWOT分析,《孙子兵法》首先不是战法,而是不战之法。首先不是战胜之法,而是不败之法
孙子兵法的计是最早的SWOT分析,<孙子兵法>首先不是战法,而是不战之法.首先不是战胜之法,而是不败之法 在打仗之前,你要详细地去算. 计算的目的是什么呢?孙子说,是为了知胜,就是为了知道 ...
随机推荐
- 使用 Postman 的 Environments 和 Tests 简化在不同环境中的切换步骤
调试 API 的时候,我们需要经常需要在本地.开发.生产来回切换,还需要面临 Token 失效等的问题,让人头大,看到一些教程有介绍用 Postman 来简化流程,但是实践起来还是遇到一些问题,所以就 ...
- C# 枚举器(enumerator)
总结: 1.枚举器就像是序列中的"游标"或"书签".可以有多个"书签",移动其中任何一个都可以枚举集合,与其他枚举器互不影响.用来遍历数据结 ...
- omnet++:官方文档翻译总结(一)
1.什么是omnet++ 翻译总结自:What is OMNeT++? omnet++是用来进行网络仿真的C++库和框架.这里的网络包括有线.无线.on-chip.queueing网络等等.特定领域中 ...
- Linux的用户与用户组管理
1.Linux用户与用户组 Linux 是多用户多任务操作系统,Linux 系统支持多个用户在同一时间内登陆,不同用户可以执行不同的任务,并且互不影响.不同用户具有不问的权限,毎个用户在权限允许的范围 ...
- 开发并发布依赖包,作为工具包供别人npm install
1.初识包及 npm 包的概念: nodejs 中的第三方模块叫包 不同于 nodejs 中的内置模块与自定义模块,包是由第三方个人或团队开发出来的,免费供所有人使用 nodejs 中的包都是免费开源 ...
- Mattermost Server安装及配置AD/LADP
一.安装Mattermost Server Mattermost is an open source, self-hosted Slack-alternative. 1.下载mattermost s ...
- Linux swap分区操作
swap交换分区是系统RAM的补充,swap 分区支持虚拟内存.当没有足够的 RAM 保存系统处理的数据时,会将数据写入 swap 分区,当系统缺乏 swap 空间时,内核会因 RAM 内存耗尽而终止 ...
- laravel7 ajax H-ui框架添加数据至数据库
1:定义路由: //租房 Route::resource('house','fang\FangattrController'); 2:控制器访问前端框架: public function create ...
- LGP2233题解
题目大意 求环上走 \(n\) 步从指定点到达另一指定点,到达指定点后 不得继续移动. 大家都做过P1057传球游戏吧?还记得这道题的思路吗? 设 \(dp[i][j]\) 表示传 \(i\) 次求传 ...
- LGP5591题解
题意很明确,不说了. 前置芝士:单位根反演 也就是: \[[n|a]=\frac 1 n \sum_{i=0}^{n-1}w_n^{ai} \] 看到题目给的柿子: \[\sum_{i=0}^n\bi ...
