BZOJ 3160 FFT+马拉车

题意显然

ans=回文子序列数目 - 回文子串数目

回文子串直接用马拉车跑出来

回文子序列一开始总是不知道怎么求 （太蠢了）

后面看了题解

构造一个神奇的卷积

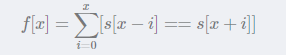（这个是我盗的图）地址

后面还有一些细节需要处理出 f[x] （f[x] 表示 x左右相等的个数）

通常我们需要的情况是 两个函数相乘 这里是s[x-i] == s[x+i] 分类讨论就行了  变成1*1=1的形式

所以要a=1 b=0 和 a=0 b=1都算一次

这里长度扩展了一倍 表示 当 i 是奇数时表示对称轴是元素 ，偶数表示对称轴是两个元素的间隔

根据二项式定理 求出每一个f[x] 的贡献 expmod ( 2, ( cnt[i] + 1 ) >> 1 ) - 1

还有最后一个细节 相减的时候要记得加上mod 再取模

 #include <cstdio>
 #include <cstring>
 #include <queue>
 #include <cmath>
 #include <algorithm>
 #include <set>
 #include <iostream>
 #include <map>
 #include <stack>
 #include <string>
 #include <vector>
 #define  pi acos(-1.0)
 #define  eps 1e-9
 #define  fi first
 #define  se second
 #define  rtl   rt<<1
 #define  rtr   rt<<1|1
 #define  bug         printf("******\n")
 #define  mem(a,b)    memset(a,b,sizeof(a))
 #define  name2str(x) #x
 #define  fuck(x)     cout<<#x" = "<<x<<endl
 #define  f(a)        a*a
 #define  sf(n)       scanf("%d", &n)
 #define  sff(a,b)    scanf("%d %d", &a, &b)
 #define  sfff(a,b,c) scanf("%d %d %d", &a, &b, &c)
 #define  sffff(a,b,c,d) scanf("%d %d %d %d", &a, &b, &c, &d)
 #define  pf          printf
 #define  FRE(i,a,b)  for(i = a; i <= b; i++)
 #define  FREE(i,a,b) for(i = a; i >= b; i--)
 #define  FRL(i,a,b)  for(i = a; i < b; i++)+
 #define  FRLL(i,a,b) for(i = a; i > b; i--)
 #define  FIN         freopen("data.txt","r",stdin)
 #define  gcd(a,b)    __gcd(a,b)
 #define  lowbit(x)   x&-x
 #define rep(i,a,b) for(int i=a;i<b;++i)
 #define per(i,a,b) for(int i=a-1;i>=b;--i)
 using namespace std;
 typedef long long  LL;
 typedef unsigned long long ULL;
 const int maxn = 3e5 + ;
 const int maxm = maxn * ;
 const int mod = 1e9 + ;
 int n, m, a[maxn], b[maxn];
 int len, res[maxm], mx; //开大4倍
 struct cpx {
     long double r, i;
     cpx ( long double r = , long double i =  ) : r ( r ), i ( i ) {};
     cpx operator+ ( const cpx &b ) {
         return cpx ( r + b.r, i + b.i );
     }
     cpx operator- ( const cpx &b ) {
         return cpx ( r - b.r, i - b.i );
     }
     cpx operator* ( const cpx &b ) {
         return cpx ( r * b.r - i * b.i, i * b.r + r * b.i );
     }
 } va[maxm], vb[maxm];
 void rader ( cpx F[], int len ) { //len = 2^M,reverse F[i] with  F[j] j为i二进制反转
     int j = len >> ;
     for ( int i = ; i < len - ; ++i ) {
         if ( i < j ) swap ( F[i], F[j] ); // reverse
         int k = len >> ;
         while ( j >= k ) j -= k, k >>= ;
         if ( j < k ) j += k;
     }
 }
 void FFT ( cpx F[], int len, int t ) {
     rader ( F, len );
     for ( int h = ; h <= len; h <<=  ) {
         cpx wn ( cos ( -t *  * pi / h ), sin ( -t *  * pi / h ) );
         for ( int j = ; j < len; j += h ) {
             cpx E ( ,  ); //旋转因子
             for ( int k = j; k < j + h / ; ++k ) {
                 cpx u = F[k];
                 cpx v = E * F[k + h / ];
                 F[k] = u + v;
                 F[k + h / ] = u - v;
                 E = E * wn;
             }
         }
     }
     if ( t == - ) //IDFT
         for ( int i = ; i < len; ++i ) F[i].r /= len;
 }
 void Conv ( cpx a[], cpx b[], int len ) { //求卷积
     FFT ( a, len,  );
     FFT ( b, len,  );
     for ( int i = ; i < len; ++i ) a[i] = a[i] * b[i];
     FFT ( a, len, - );
 }
 void gao () {
     len = ;
     mx = n + m;
     while ( len <= mx ) len <<= ; //mx为卷积后最大下标
     for ( int i = ; i < len; i++ ) va[i].r = va[i].i = vb[i].r = vb[i].i = ;
     for ( int i = ; i < n; i++ ) va[i].r = a[i]; //根据题目要求改写
     for ( int i = ; i < m; i++ ) vb[i].r = b[i]; //根据题目要求改写
     Conv ( va, vb, len );
     for ( int i = ; i < len; ++i ) res[i] += ( LL ) floor ( va[i].r + 0.5 );
 }
 char Ma[maxn * ];
 int Mp[maxn * ];
 int Manacher ( char s[], int len ) {
     int l = , ret = ;
     Ma[l++] = '$';
     Ma[l++] = '#';
     for ( int i = ; i < len; i++ ) {
         Ma[l++] = s[i];
         Ma[l++] = '#';
     }
     Ma[l] = ;
     int mx = , id = ;
     for ( int i = ; i < l; i++ ) {
         Mp[i] = mx > i ? min ( Mp[ * id - i], mx - i ) : ;
         while ( Ma[i + Mp[i]] == Ma[i - Mp[i]] ) Mp[i]++;
         if ( i + Mp[i] > mx ) {
             mx = i + Mp[i];
             id = i;
         }
         ret += Mp[i] >> , ret %= mod;
     }
     return ret % mod;
 }
 LL expmod ( LL a, LL b ) {
     LL res = ;
     while ( b ) {
         if ( b &  )  res = res * a % mod;
         a = a * a % mod;
         b = b >> ;
     }
     return res % mod;
 }
 char s[maxn];
 int cnt[maxn];
 int main() {
    // FIN;
     scanf ( "%s", s +  );
     n = m = strlen ( s +  );
     LL ans = , temp = Manacher ( s + , n );
     n++, m++;
     for ( int i =  ; i < n  ; i++ ) if ( s[i] == 'a' ) a[i] = , b[i] = ;
     gao();
     for ( int i =  ; i <=  * ( n -  ) ; i++ ) cnt[i] += res[i];
     mem ( a,  ), mem ( b,  ), mem ( res,  );
     for ( int i =  ; i < n  ; i++ ) if ( s[i] == 'b' ) a[i] = , b[i] = ;
     gao();
     for ( int i =  ; i <=  * ( n -  ) ; i++ ) cnt[i] += res[i];
     for ( int i =  ; i <=  * ( n -  ) ; i++ )
         ans = ( ans + expmod ( , ( cnt[i] +  ) >>  ) -  ) % mod;
     printf ( "%lld\n", ( ans - temp + mod ) % mod );
     return ;
 }