第一步：输入目标条件和约束条件。每行以分号隔开。然后点击工具栏上的Solve按钮，或Lingo菜单下的Solve子菜单。

第二步：检查report中的结果。

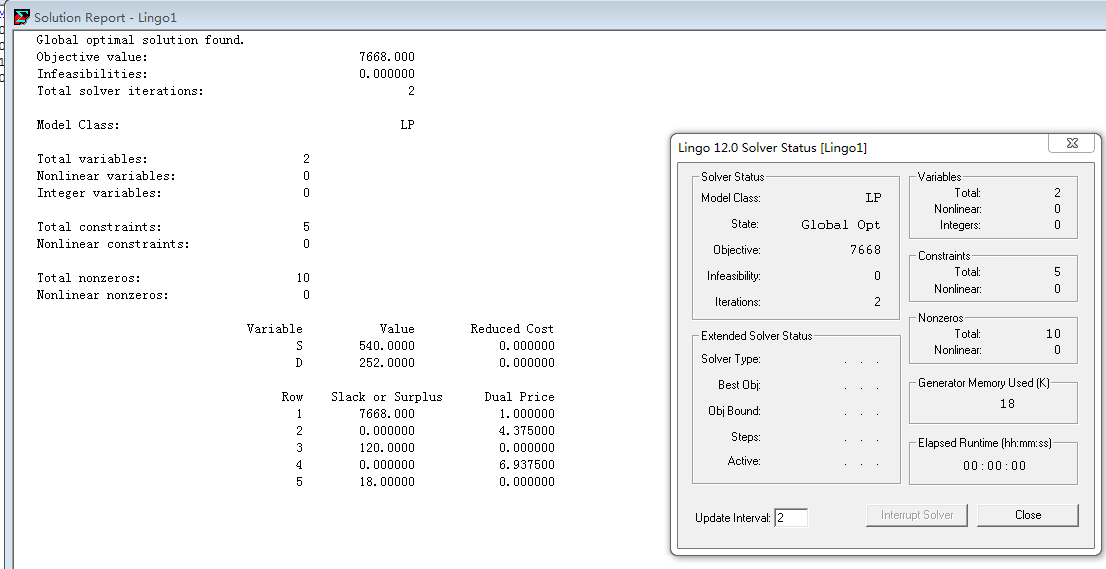
默认情况下，Lingo不进行灵敏度分析。

需要在Lingo中一下配置才可以生成灵敏度分析报告：Lingo菜单》Options. General Solver选项卡》Dual Computations:Prices and Ranges. 然后点击Apply按钮。

重新点击Solve菜单和Range菜单以生成如下灵敏度分析报告（Range Report）

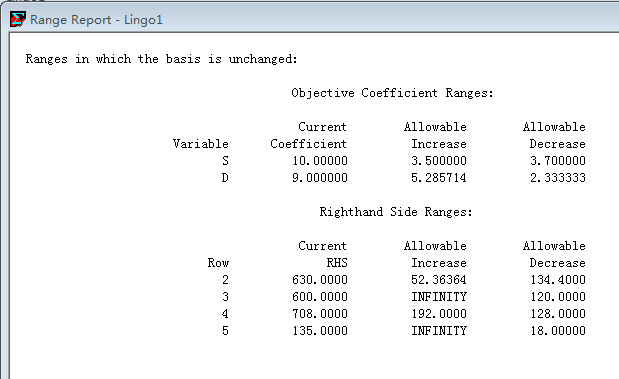
用Lingo求解线性规划问题的更多相关文章

  1. Lingo求解线性规划案例4——下料问题

    凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/ 造纸厂接到定单,所需卷纸的宽度和长度如表 卷纸的宽度 长度 5 7 9 10000 30000 20000 工 ...

  2. Lingo求解线性规划案例1——生产计划问题

    凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/ 说明: Lingo版本:                            某工厂明年根据合同,每个季度末 ...

  3. Lingo求解线性规划案例3——混料问题

    凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/  某糖果厂用原料A.B和C按不向比率混合加工而成甲.乙.丙三种糖果(假设混合加工中不损耗原料).原料A.B.C ...

  4. Lingo求解线性规划案例2——多阶段投资问题

     凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/ 某公司现有资金30万元可用于投资,5年内有下列方案可供采纳:   1号方案:在年初投资1元,2年后可收回1. ...

  5. 图论中最优树问题的LINGO求解

    树:连通且不含圈的无向图称为树.常用T表示.树中的边称为树枝,树中度为1的顶点称为树叶. 生成树:若T是包含图G的全部顶点的子图,它又是树,则称T是G的生成树. 最小生成树:设T=(V,E1)是赋权图 ...

  6. matlab学习笔记之求解线性规划问题和二次型问题

    一.线性规划问题 已知目标函数和约束条件均为线性函数,求目标函数的最小值(最优值)问题. 1.求解方式:用linprog函数求解 2.linprog函数使用形式: x=linprog(f,A,b)  ...

  7. matlab 求解线性规划问题

    线性规划 LP(Linear programming,线性规划)是一种优化方法,在优化问题中目标函数和约束函数均为向量变量的线性函数,LP问题可描述为: minf(x):待最小化的目标函数(如果问题本 ...

  8. Python求解线性规划——PuLP使用教程

    简洁是智慧的灵魂,冗长是肤浅的藻饰.--莎士比亚<哈姆雷特> 1 PuLP 库的安装 如果您使用的是 Anaconda[1] 的话(事实上我也更推荐这样做),需要先激活你想要安装的虚拟环境 ...

  9. 单纯形求解线性规划(BZOJ1061)

    推荐一篇论文:http://wenku.baidu.com/view/ce5784754a7302768f99391d 我们设xi为第i个志愿者的招募次数,以样例为例,则不难列出如下的线性规划方程: ...

随机推荐

  1. 2018.08.28 洛谷P4556 [Vani有约会]雨天的尾巴（树上差分+线段树合并）

    传送门 要求维护每个点上出现次数最多的颜色. 对于每次修改,我们用树上差分的思想,然后线段树合并统计答案就行了. 注意颜色很大需要离散化. 代码: #include<bits/stdc++.h& ...

  2. 2018.07.24 bzoj3531: [Sdoi2014]旅行（树链剖分+动态开点）

    传送门 树链剖分. 如何维护? 如果颜色少直接每种颜色一颗线段树走人. 但这题颜色数量不大于1e5" role="presentation" style="po ...

  3. Stacktraces java.lang.NoSuchMethodException: com.liuyang.action.UserAction.add()

    Struts Problem Report Struts has detected an unhandled exception: Messages: com.liuyang.action.UserA ...

  4. ROM初始化HEX文件

    intel hex格式 记录格式 Intel HEX由任意数量的十六进制记录组成.每个记录包含5个域,它们按以下格式排列: :llaaaatt[dd...]cc 每一组字母对应一个不同的域,每一个字母 ...

  5. 修改Python IDLE代码配色及语法高亮主题

    初学Python,想必大家拿来练习最多的IDE就是Python自带的IDLE了,但是默认的代码配色及语法高亮主题确实很不适应,所以我们需要做个小小的美化,比如像下面这样我做的美化配置: HOW TO ...

  6. 微信post xml 消息编码问题

    site:mp.weixin.qq.com utf 微信卡券接口说明 - 微信公众平台开发者文档 所有API接口POST的数据只支持utf8编码,否则会返回报错. 以上是获取的部分信息 这个尽管有点模 ...

  7. faceswap使用手冊

    cd faceswap cd faceswap-master python faceswap.py gui Notice: This repository is not operated or mai ...

  8. aop的概述

    支付部分,定义IPayService接口并定义支付方法“pay”,并定义了两个实现:“PointPayService”表示积分支付,“RMBPayService”表示人民币支付:并且在每个支付实现中支 ...

  9. delphi 使用oauth的控件

    unit OAuth; interface uses Classes, SysUtils, IdURI, Windows; type EOAuthException = class(Exception ...

  10. eclipse/myeclipse介绍

    eclipse更加纯净,比较简洁,需要某些插件的时候,需要自己去配置才可以,而myeclipse自带了很多的插件功能更为强大. 在eclipse于myeclipse创建的项目是有差异的,eclipse ...