The Limitations of Deep Learning in Adversarial Settings

目录

• 概
• 主要内容
  • alg2, alg3
  • 一些有趣的实验指标
    • Hardness measure
    • Adversarial distance

Nicolas Papernot, Patrick McDaniel, Somesh Jha, Matt Fredrikson, Z. Berkay Celik, Ananthram Swami, The Limitations of Deep Learning in Adversarial Settings.

概

利用Jacobian矩阵构造adversarial samples，计算量比较大.

主要内容

目标:

\[\tag{1}
\mathop{\arg \min} \limits_{\delta_X} \|\delta_X\|, \mathbf{s.t.} \: F(X+\delta_X)=Y^*.
\]

简而言之, 在原图像\(X\)上加一个扰动\(\delta_X\), 使得\(F\)关于\(X+\delta_X\)的预测为\(Y^*\)而非\(Y\).

若\(Y \in \mathbb{R}^M\)是一个\(M\)维的向量, 类别由下式确定

\[label(X)=\mathop{\arg \min} \limits_{j} F_j(X).
\]

\(F(X)=Y\)关于\(X\)的Jacobian矩阵为

\[[\frac{\partial F_j(X)}{\partial X_i}]_{i=1,\ldots,N,j=1,\ldots,M},
\]

注意, 这里作者把\(X\)看成一个\(N\)维向量(只是为了便于理解).

因为我们的目的是添加扰动\(\delta_X\), 使得\(X+\delta_X\)的标签为我们指定的\(t\), 即我们希望

\[t=\mathop{\arg \min} \limits_{j} F_j(X+\delta_X).
\]

作者希望改动部分元素, 即\(\|\delta_X\|_0\le \Upsilon\), 作者是构造了一个saliency_map来选择合适的\(i\), 并在其上进行改动, 具体算法如下:

saliency_map的构造之一是:

\[S(X,t)[i] = \{
\begin{array}{ll}
0, & if \: \frac{\partial{F_t(X)}}{\partial X_i} <0 \:or \: \sum_{j \not= t} \frac{\partial F_j(X)}{\partial X_i} >0, \\
\frac{\partial{F_t(X)}}{\partial X_i} |\sum_{j \not= t} \frac{\partial F_j(X)}{\partial X_i}|, & otherwise.
\end{array}
\]

可以很直观的去理解, 改变标签, 自然希望\(F_t(X)\)增大, 其余部分减少, 故 \(\frac{\partial{F_t(X)}}{\partial X_i} <0 \:or \: \sum_{j \not= t} \frac{\partial F_j(X)}{\partial X_i} >0\)所对应的\(X_i\)自然是不重要的, 其余的是重要的, 其重要性用\(\frac{\partial{F_t(X)}}{\partial X_i} |\sum_{j \not= t} \frac{\partial F_j(X)}{\partial X_i}|\)来表示.

alg2, alg3

作者顺便提出了一个更加具体的算法, 应用于Mnist, max_iter 中的\(784\)即为图片的大小\(28 \times 28\), \(\Upsilon=50\), 相当于图片中\(50\%\)的像素发生了改变, 且这里采用了一种新的saliency_map, 其实质为寻找俩个指标\(p,q\)使得:



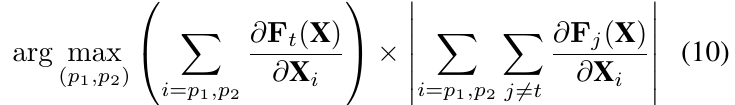
其实际的操作流程根据算法3. \(\theta\)是每次改变元素的量.

一些有趣的实验指标

Hardness measure

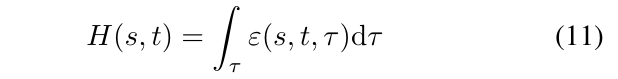
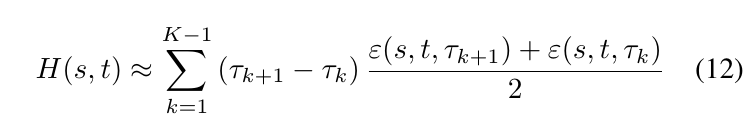
其中\(\epsilon(s,t,\tau)\)中, \(s\):图片标签, \(t\):目标标签, \(\tau\):成功率, \(\epsilon\)为改变像素点的比例. (12)是(11)的一个梯形估计, \(\tau_k\)由选取不同的\(\Upsilon_k\)来确定, \(H(s, t)\)越大说明将类别s改变为t的难度越大.

Adversarial distance

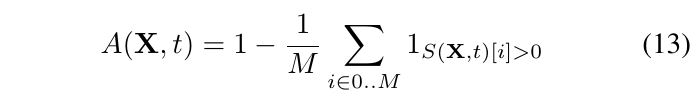
\(A(X,t)\)越大, 说明将图片\(X\)的标签变换至\(t\)的难度越大, 而一个模型的稳定性可以用下式衡量

\[\tag{14}
R(F)=\min_{X,t} A(X,t).
\]