Shadertoy 教程 Part 3 - 矩形和旋转

Note: This series blog was translated from Nathan Vaughn's Shaders Language Tutorial and has been authorized by the author. If reprinted or reposted, please be sure to mark the original link and description in the key position of the article after obtaining the author’s consent as well as the translator's. If the article is helpful to you, click this Donation link to buy the author a cup of coffee.

说明：该系列博文翻译自Nathan Vaughn的着色器语言教程。文章已经获得作者翻译授权，如有转载请务必在取得作者和译者同意之后在文章的重点位置标明原文链接以及说明。如果你觉得文章对你有帮助，点击此打赏链接请作者喝一杯咖啡。

朋友们，你们好！在上一篇文章中，我们学习了如何绘制一个圆形并且让它动起来。在这篇文章中，我们将会学习如何绘制一个方块并且用一个旋转矩阵让它转起来。

绘制矩形

绘制一个矩形和绘制一个圆形是非常相似的，我们只需要用另外一个等式。实际上，只需要我们写出一个正确的等式，我们就能几乎能绘制出它对应的图形。矩形的等式如下：

  max(abs(x),abs(y)) = r

  x = x-coordinate on graph
  y = y-coordinate on graph
  r = radius of square

我们调整等式和变量的顺序，使得等式为0：

  max(abs(x), abs(y)) - r = 0

我们把它改造成下面的样子，就可以Desmos calcultor生成可视化的图形公式了：

max(abs(x), abs(y)) - 2 = 0

复制上面的代码，然后把它粘贴到Desmos calculator中，你就能看到一个半径为2的正方形，它的中心点在原点（0,0）上。

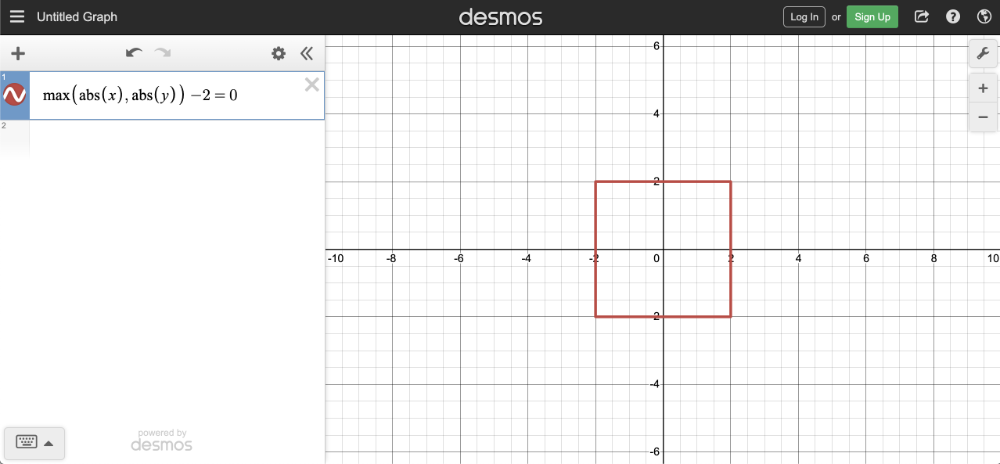
你也可以给它设置一些偏移值：

max(abs(x - offsetX), abs(y - offsetY)) - r = 0

offsetX = how much to move the center of the square in the x-axis
offsetY = how much to move the center of the square in the y-axis

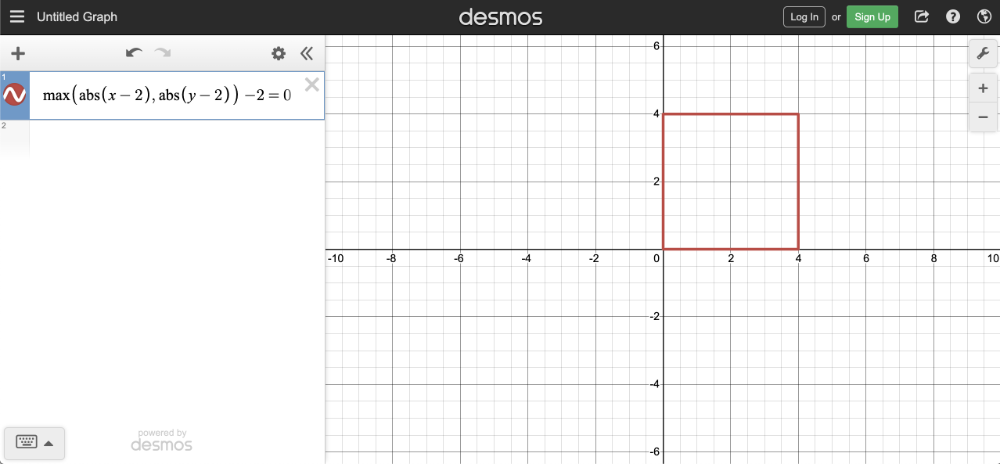
使用像素着色器绘制一个正方形的步骤和我们在上一节教程中讲到的绘制一个圆的步骤十分相似，我们给正方形构建一个指定的函数：

  vec3 sdfSquare(vec2 uv, float size, vec2 offset) {
  float x = uv.x - offset.x;
  float y = uv.y - offset.y;
  float d = max(abs(x), abs(y)) - size;

  return d > 0. ? vec3(1.) : vec3(1., 0., 0.);
}

void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
  vec2 uv = fragCoord/iResolution.xy; // <0, 1>
  uv -= 0.5; // <-0.5,0.5>
  uv.x *= iResolution.x/iResolution.y; // fix aspect ratio

  vec2 offset = vec2(0.0, 0.0);

  vec3 col = sdfSquare(uv, 0.2, offset);

  // Output to screen
  fragColor = vec4(col,1.0);
}

哇！我们得到了一个红色正方形 ！

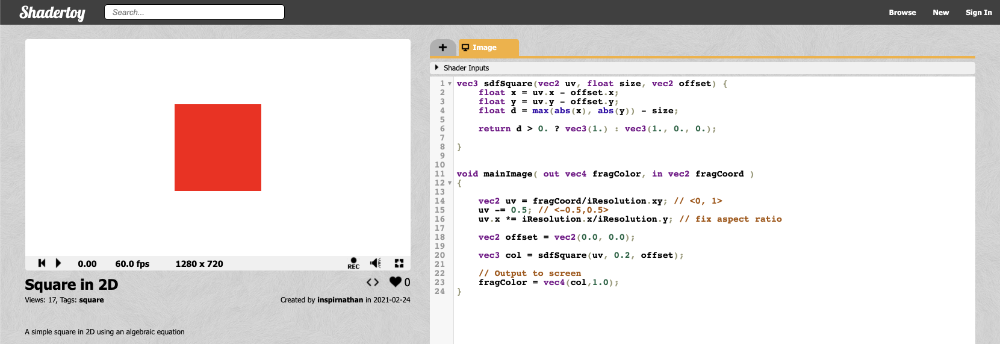
让正方形转起来

使用下面的表示法构建一个旋转矩阵，就可以让我们的图形转起来：

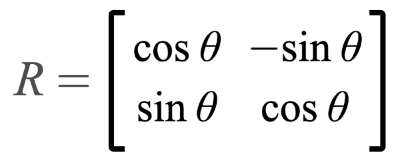
矩阵帮助我们处理线性方程和线性变换。实际上，一个旋转矩阵就是仿射变换矩阵的一种类型。我们可以使用矩阵来处理其他的放射变换例如：剪切、变形或者反射。

提示： 如果你想要试试矩阵计算，你可以使用Demos Matrix Calculator 或者 WolframAlpha。如果你要复习一下矩阵知识，你可以观看Derek Banas 在YouTuBe上发布的这个神奇的视频。

你可以使用我在Desmos上创建的一个可视化旋转图形。我用旋转矩阵创建了一系列的线性方程式，在这些方程式中都使用旋转矩阵。

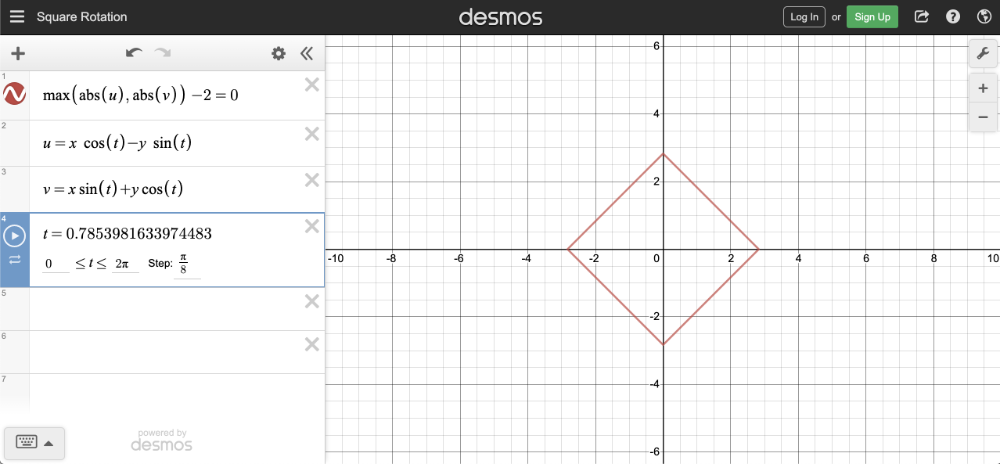
用旋转矩阵乘以WolfraAlpha中计算后得出的向量[x，y]就能得到线性方程式。其结果就是结果就是一个转换了X和Y坐标的等式。

在Shadertoy中，我们只需要关系旋转矩阵，而不是线性方程式。我也只会在讨论在Desmos中展示旋转示例的时候提及到它。

我们创建一个旋转矩阵函数，这个矩阵接受UV坐标以及一个角度用来旋转正方形。它的返回结果是一个乘以UV坐标后的旋转矩阵。然后，我们在sdfSquare函数中调用rotate函数，给它传递我们的XY坐标，或者一个它的偏移值（如果它存在的话）。我们将使用到iTime作为角度，这样正方形就能动起来。

  vec2 rotate(vec2 uv, float th) {
  return mat2(cos(th), sin(th), -sin(th), cos(th)) * uv;
}

vec3 sdfSquare(vec2 uv, float size, vec2 offset) {
  float x = uv.x - offset.x;
  float y = uv.y - offset.y;
  vec2 rotated = rotate(vec2(x,y), iTime);
  float d = max(abs(rotated.x), abs(rotated.y)) - size;

  return d > 0. ? vec3(1.) : vec3(1., 0., 0.);
}

void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
  vec2 uv = fragCoord/iResolution.xy; // <0, 1>
  uv -= 0.5; // <-0.5,0.5>
  uv.x *= iResolution.x/iResolution.y; // fix aspect ratio

  vec2 offset = vec2(0.0, 0.0);

  vec3 col = sdfSquare(uv, 0.2, offset);

  // Output to screen
  fragColor = vec4(col,1.0);
}

请注意我们是如何在Shadertoy中定义矩阵的。让我们更近地观察旋转函数吧。

  vec2 rotate(vec2 uv, float th) {
  return mat2(cos(th), sin(th), -sin(th), cos(th)) * uv;
}

根据维基百科上的GLSL规范，我们定义一个由逗号分隔各个值的矩阵，我们需要先看列。因为这个矩阵是mat2类型的，它就是一个2*2的矩阵。前面的两个值表示为第一列，后面两个值表示第二列。在WolframAlpha这种工具中，你需要首先插入行值让后用方括号分隔它们。在使用度量的时候一定要记住这点。

我们的rotate函数返回一个vec2类型的向量，因为2乘2的矩阵（mat2）乘以一个vec2的向量返回的是另外一个vec2向量。

运行以上代码，我们就可以看到一个沿着顺时钟旋转的正方形了。

总结

在这节课中，我们学会了如何绘制一个圆并且使用变形矩阵让它动起来。运用你本节和上一节课学习到的知识，使用一个SDF公式绘制出你自己的2D图形吧！

在下一篇文章中，我将会讨论如何在画布上绘制多种形状，同时也会讨论如何改变背景颜色。

资源

• 2D Rotation Example
• Vector and Matrix Operations in GLSL
• Vector and Matrix Transformations
• Matrix Arithmetic
• 2D SDFs